Формула Бернулли, полная вероятность

тема «Формула полной вероятности»

1. Студент знает билета из . В каком случае вероятность вытащить счастливый билет для него больше, если он идет сдавать экзамен первым или вторым?

2. Семь студентов, получив билеты готовятся к ответу экзаменатору. Знание билета гарантирует сдачу экзамена с вероятностью , незнание с вероятностью . Какова вероятность того, что вызванный наудачу студент сдаст экзамен, если Иванов знает билетов из , Петров – лишь , а остальные студенты знают все билеты?

3. В первой урне находится белых и черных шаров, а во второй белых и черных шаров. Из первой урны наудачу перекладывают во вторую два шара, а затем из второй урны извлекают один шар. Какова вероятность того, что он окажется белым?

4. Имеются три партии деталей по деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно , 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найдите вероятность того, что детали были извлечены из третьей партии.

5. Планируется ракетный залп по кораблю противника. Вероятность попадания каждой ракеты в цель равна 0,4. Вероятность поражения корабля при попадании одной, двух, трех, четырех ракет соответственно равна 03; 0,4; 0,5; 0,6.Найдите вероятность поражения корабля.

6. В условиях задачи № 6 корабль был поражен. Какова вероятность того, что он был поражен попаданием трех ракет?

7. Из сдающих экзамен студентов семеро знают все билетов, двое знают по билетов и один знает билетов. Знание билета гарантирует сдачу экзамена с вероятностью , незнание с вероятностью . Какова вероятность того, что первый вызванный наудачу студент сдаст экзамен?

8. В урну, содержащую два шара опущен белый шар, после чего из нее наудачу извлечен шар. Найдите вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном цвете шаров.

9. Военный корабль может пройти вдоль пролива шириной 1 км с минным заграждением в любом месте. Вероятность его подрыва на мине в правой части заграждения шириной 200 м равна 0,3, а на остальной части – 0,8. Найдите вероятность того, что корабль благополучно пройдет пролив.

10. В торговую фирму поставляются телевизоры тремя фирмами в соотношении 5:2:3. Телевизоры, поступающие от этих фирм не требуют ремонта в течение гарантийного срока соответственно в 96%, 92%, и 94% случаев. Найдите вероятность того, что купленный наудачу телевизор не потребует ремонта в течение гарантийного срока.

11. В условиях задачи № 5 купленный телевизор не потребовал ремонта в течение гарантийного срока. Какая фирма вероятнее всего поставила данный телевизор?

Тема «Формула Бернулли».

1. Игральную кость подбрасывают 8 раз. Какова вероятность того, что 5 раз выпадут одинаковые числа?

2. Проводятся десять испытаний Бернулли с вероятностью успеха . Найдите вероятность того, что число успехов больше , но меньше .

3. Пусть вероятность того, что студент опоздает на лекцию равна 0.08. Найти наиболее вероятное число опоздавших из 96 студентов.

4. Проводится неограниченное число испытаний Бернулли с вероятностью успеха 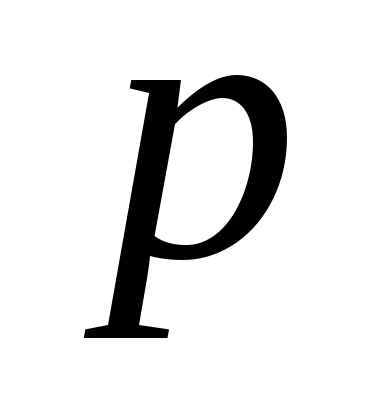. Найдите вероятность того, что серия из двух последовательных успехов наступит раньше серии из двух последовательных неудач.

5. Проводятся десять испытаний Бернулли с вероятностью успеха . Какова вероятность того, что число успехов в первой половине испытаний на два больше числа успехов во второй половине испытаний?

6. Всхожесть семян данного сорта растений составляет 70%. Найти наивероятнейшее число всхожих семян из партии в 240 семян.