снижается на величину eU по сравнению с равновесным состоянием и уменьшается толщина р-п-перехода (рис. 2.2в). При обратном подключении источника питания к р-п-переходу (минус к р-области) потенциальный барьер повышается на величину eU и увеличивается толщина р-п-перехода (рис. 2.2г). В общем случае произвольного значения напряжения смещения выражение для ширины р-п-перехода (2.7) может быть преобразовано к виду:

Здесь знаки «–» и «+» соответствуют напряжениям прямого и обратного смещения на р-п-переходе.

2.2. Барьерная емкость р-п-перехода

Изменение ширины области р-п-перехода при приложении к нему напряжения смещения приводит к изменению заряда двойного электрического слоя, образованного отрицательно заряженными акцепторами в дырочном и положительно заряженными донорами в электронном полупроводниках. Это означает, что р-п-переход обладает электроемкостью. Эта емкость

получила название барьерной емкости р-п-перехода, поскольку заряд dQ , появление которого связано изменением напряжения

dU , располагается в области потенциального барьера р-п- перехода.

Выражение для заряда dQ в п-области перехода с учетом

где S – площадь р-п-перехода; dLn – ширина области, где располагается заряд ионизированных доноров dQ ; dL –

приращение ширины области р-п-перехода при изменении напряжения на нем на dU .

Подставляя (2.10) в (2.9) и принимая во внимание (2.8), получим окончательное выражение для барьерной емкости р-п-

Формула для барьерной емкости р-п-перехода (2.11) имеет такой же вид, что и формула для емкости плоского конденсатора. Это объясняется тем, что при изменении напряжения на р-п- переходе на dU заряды ионизированных доноров и акцепторов изменяются на одинаковую по модулю величину dQ , причем эти

заряды, противоположные по знаку, располагаются на расстоянии L друг от друга. Барьерная область р-п-перехода при этом играет роль своеобразного диэлектрика. Эта ситуация аналогична ситуации с плоским конденсатором, в котором заряд располагается на металлических обкладках, разделенных слоем диэлектрика.

Однако, несмотря на внешнее сходство формул для барьерной емкости и емкости плоского конденсатора, физические свойства этих емкостей различаются. Так, емкость плоского конденсатора не зависит от приложенного напряжения, в то время как барьерная емкость р-п-перехода существенно зависит от напряжения. В этом легко убедиться, подставив в (2.11) выражение для толщины барьерного слоя (2.8):

Анализ формулы (2.12) показывает, что с увеличением напряжения обратного смещения (используется знак «+») барьерная емкость уменьшается, а с увеличением напряжения прямого смещения (используется знак «–») барьерная емкость

увеличивается. При изменении прямого смещения р-п-перехода, кроме изменения заряда ионизированных примесей внутри перехода, происходит изменение заряда подвижных носителей, которое приводит к появлению так называемой диффузионной емкости. Вопрос о диффузионной емкости здесь рассматриваться не будет.

2.3. Выпрямление на р-п-переходе

Между р- и п-областями р-п-перехода происходит обмен свободными носителями заряда. Наличие градиента концентрации дырок и электронов приводит к протеканию через р-п-переход диффузионного тока основных носителей Iдифф

(дырок из р-области в п-область и электронов в противоположном направлении). Дырки, перешедшие в п- область, а электроны – в р-область являются уже там неосновными носителями заряда. В условиях динамического равновесия через р-п-переход проходят только те свободные носители заряда, энергия которых больше высоты потенциального барьера. Концентрации свободных дырок и электронов, способных преодолеть потенциальный барьер, высота которого определяется контактной разностью потенциалов eϕk , могут быть записаны соответственно в виде

области соответственно.

Одновременно с движением основных носителей заряда через р- п-переход движутся неосновные носители заряда, причем их поток противоположен потоку основных носителей (электроны переходят из области р-типа в область п-типа, а дырки – в противоположном направлении). Для неосновных носителей заряда в области р-п-перехода нет потенциального барьера,

наоборот, если благодаря тепловому движению неосновной носитель заряда попадает в область р-п-перехода, то электрическое поле в нем способствует его движению из одной области полупроводника в другую. Поток неосновных носителей заряда через р-п-переход создает дрейфовый ток Iдр . В условиях

равновесия диффузионный и дрейфовый токи по абсолютной величине равны, а так как они направлены в противоположные стороны, то результирующий ток I через р-п-переход будет равен нулю ( I = Iдифф − Iдр = 0 ).

При смещении р-п-перехода в прямом направлении (положительный потенциал на р-области) ток неосновных носителей заряда остается практически неизменным, в то время как ток основных носителей заряда возрастает. Это связано с тем, что высота потенциального барьера понижается на величину eU и, следовательно, большее число дырок может перейти из р- области в п-область и большее число электронов – из п-области в р-область. В этом случае выражения (2.13) преобразуются к виду

где pn и n p – концентрации дырок в п-области и электронов в р-

области соответственно при подаче на р-п-переход напряжения U в прямом направлении.

Выражения (2.13) и (2.14) позволяют найти неравновесные концентрации неосновных носителей заряда, которые появились вблизи р-п-перехода при его прямом смещении, а именно:

где ∆p и ∆n – неравновесные концентрации дырок и электронов соответственно.

Неравновесные дырки ∆p , появившиеся в п-области,

создадут в первый момент вблизи р-п-перехода положительный объемный заряд. Однако через короткое время, называемым максвелловским временем релаксации, этот заряд будет скомпенсирован объемным зарядом основных носителей – электронов, которые под действием электрического поля, созданного неравновесными дырками, будут подтянуты из глубины п-области, а в п-область электроны поступят из внешней цепи. Аналогично произойдет и нейтрализация отрицательного заряда неравновесных электронов ∆n в р-области. Таким образом, во всех частях полупроводника, кроме обедненной свободными носителями заряда области р-п-перехода, будет соблюдаться электронейтральность.

Введение в полупроводник неравновесных носителей заряда с помощью р-п-перехода при подаче на него прямого смещения называется инжекцией. Из анализа выражений (2.15) следует, что с увеличением прямого смещения на р-п- переходе концентрация инжектируемых неосновных носителей заряда резко возрастает, что приводит к сильному росту тока через переход в прямом направлении (рис. 2.3). Ток прямосмещенного р-п-перехода называется прямым током. Поскольку концентрация неравновесных неосновных носителей заряда растет экспоненциально с напряжением (2.15), то даже при сравнительно небольшом прямом смещении ( eU ~ 3kT ) диффузионный ток на порядок превысит дрейфовый. В этом случае I ≈ Iдифф .

При подаче напряжения обратного смещения на р-п- переход увеличивается высота потенциального барьера и, следовательно, меньшее количество основных носителей заряда будет способно его преодолеть. Концентрации дырок в р-области и электронов в п-области по-прежнему определяются равенствами (2.14), но значение напряжения U здесь уже берется с отрицательным знаком. В соответствии с этим количество неосновных носителей заряда вблизи р-п-перехода уменьшается по сравнению с их равновесным значением, что приводит к такому же уменьшению количества основных носителей заряда, вследствие соблюдения электронейтральности в этой области полупроводника. Уменьшение концентрации неосновных носителей заряда вблизи р-п-перехода при его включении в обратном направлении носит название экстракции носителей заряда.

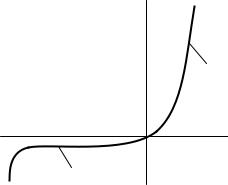
I

Прямая

ветвь

U

Обратная

ветвь

Рис. 2.3. Вольт-амперная характеристика р-п-перехода.

В связи с тем, что с увеличением высоты потенциального барьера уменьшается число основных носителей заряда, способных преодолеть барьер, уменьшается диффузионный ток. Дрейфовый ток, обусловленный движением неосновных носителей заряда, остается при этом неизменным.

направлением дрейфовой составляющей. Ток обратносмещенного р-п-перехода называется обратным током. Обратный ток через р- п-переход с увеличением обратного напряжения вначале растет по модулю за счет уменьшения диффузионного тока, а затем стремится к насыщению (рис. 2.3). В области насыщения I ≈ −Iдр , т.к. вклад диффузионного тока при большом значении

обратного напряжения становится незначительным. Кроме этого, в обратный ток дают вклад электронно-дырочные пары, генерируемые в области р-п-перехода.

Зависимость тока через р-п-переход от приложенного к нему напряжения называется его вольт-амперной характеристикой. Уравнение этой характеристики имеет следующий вид

где I нас – ток насыщения.

Уравнение (2.16), описывающее ток, протекающий через р-п- переход, по своей структуре подобно уравнению для неравновесных неосновных носителей заряда (2.15), что, как это следует из анализа предыдущих рассуждений, не является случайным. Асимметрия вольт-амперной характеристики р-п- перехода относительно полярности напряжения используется в полупроводниковых диодах для выпрямления переменного тока.