Глава 4

Основы теории размерностей и подобия. Моделирование явлений переноса

Явления природы не зависят от выбора системы единиц измерения и размеров единиц. Такими же свойствами обладают и уравнения математической физики, если они верно выражают свойства явлений.

Это основное положение, используемое при приведении зависимостей к безразмерному виду, и основная аксиома теории подобия.

§ 4.1. Понятие о физическом подобии

Два физических процесса называют подобными, если:

1) два процесса имеют качественно одинаковые условия однозначности;

2) сходственные величины обоих процессов связаны друг с другом преобразованием подобия;

3) математические описания обоих процессов также связаны преобразованием подобия.

Качественно одинаковыми называются процессы, имеющие одинаковую физическую природу и одинаковые математические описания. Эти описания совпадают друг с другом во всем, кроме численных значений физических величин, входящих в условия однозначности.

Преобразованием подобия называют линейное соотношение, которое связывает сходственные величины

j₁ = C_j j₂.

Величины j₁ и j₂ называют сходственными, если они имеют:

а) одинаковый физический смысл;

б) характеризуют процессы 1 и 2 в сходственных точках пространства и в сходственные моменты времени.

В одинаковой системе отсчета сходственные точки пространства имеют пропорциональные друг другу координаты

x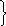₁ = С_l x₂

y₁ = С_l y₂ , l₁ = C_ll₂.

z₁ = C_l z₂

Сходственные моменты времени имеют одинаковое начало отсчета, они пропорциональны друг другу: ₁ = С_₂.

Коэффициент С называют константой подобия. По определению константы обладают следующими свойствами:

а) они безразмерны;

б) конечны и положительны;

в) не зависят ни от координат, ни от времени, ни от направления;

г) одинаковы для однородных величин и, вообще говоря, различны для величин неоднородных.

Пример физического подобия: нестационарная теплопроводность (гл.3), два процесса в двух тонких пластинах:

f(x₁, ₁, V₁,t₁, ₁, ₁, a₁, ₁) = 0;

f(x₂, ₂, V₂, t₂, ₂, ₂, a₂, ₂) = 0;

x₁ = c_l x₂; V₁ = C_tV₂;

₁ = c_l ₂; t₁ = C_tt₂ и т.д.

§ 4.2. Теоремы подобия

Прямая теорема подобия

Если физические процессы подобны, то их одноименные критерии подобия имеют одинаковую величину: ₁ = idem, _i . . ., _п-к = idem.

Эта теорема устанавливает признаки сходства подобных явлений.

Обратная теорема подобия

Для того, чтобы физические процессы были подобны друг другу, достаточно, чтобы они были качественно одинаковы, а их одноименные определяющие критерии подобия имели одинаковую величину. Эта теорема устанавливает достаточные условия для подобия явлений и является базой для физического моделирования.

-теорема

Если уравнение f(а₁а₂...а_п) = 0 содержит n размерных величин с независимыми друг от друга единицами измерения, то это уравнение приводится к безразмерному виду F(₁₂..._п-к) = 0, которое содержит n-к безразмерных величин . Данная теорема является базовой для приведения размерных зависимостей к обобщающему безразмерному виду и позволяет проверить правильность такого преобразования.

Пример использования -теоремы. Нестационарная температура в тонкой пластине, описываемая зависимостью из восьми размерных величин (n = 8):

f(x, , V, t, , , a, ) = 0.

Здесь количество групп размерных величин с независимыми размерностями равно четырем (k = 4). Тогда уравнение приводится к виду:

F(, X, Fо, Bi) = 0,

где число безразмерных величин равно четырем (n – k) = 4.

Пример тепловой модели (использования обратной теоремы).

Нагретый стальной шар погружают в закалочную масляную ванну. Необходимо промоделировать поле температуры при нестационарной теплопроводности в этом шаре на модели, выполненной из бетона и охлаждаемой воздухом.

Образец (сталь)	Модель (бетон)
1 = 4,0 c1 = 0,1 1 = 7900 d01 = 200 мм 1 = 500 tж1 = 200 0C t01 = 600 0C	2 = 1,1 c2 = 0,27 2 = 2300 d02 = 276 мм 2 = 10 tж2 = 10 0С t02 = 100 0C

Так как процесс нестационарной теплопроводности, то безразмерные критерии связаны соотношением

;

.

Используем обратную теорему подобия: Bi₁ = Bi₂,

;

, т.е. С_l = 0,725.

Тогда из Fo₁ = Fo₂

, так как ;

, t₁ = 5t₂ + 100.

Измеряем на модели r₂ t₂ t₁ при соответствующем значении r₁.

Контрольные вопросы

1. Объяснить различия между прямой и обратной основными теоремами теории подобия.

2. Привести примеры констант подобия из тепловой модели закаливаемого в масляной ванне шара.

3. Как используется -теорема при приведении уравнения к безразмерному виду?

§ 4.3. Использование методов подобия для приведения уравнений к безразмерному виду

Основными методами приведения зависимости к безразмерному виду являются:

1) метод преобразования масштабов;

2) метод анализа размерностей;

3) метод критериальных отношений.

Пример 1. Привести зависимость нестационарного поля избыточной температуры V = t_ж  t для случая нагрева тонкой пластины к безразмерному виду, не решая уравнений.

Используем метод преобразования масштабов.

Математическое описание процесса для нестационарной теплопроводности для избыточной (разностной) температуры V = t_ж – t имеет вид

Задача содержит три переменных: V, x, . Запишем их в безразмерном виде:

.

Величины t, , ₀ имеют смысл единиц измерения или масштабов температуры, расстояния, времени (заметим, что масштаб ₀ условиями задачи не задается). Находим, что , и подставляем в математическое описание задачи.

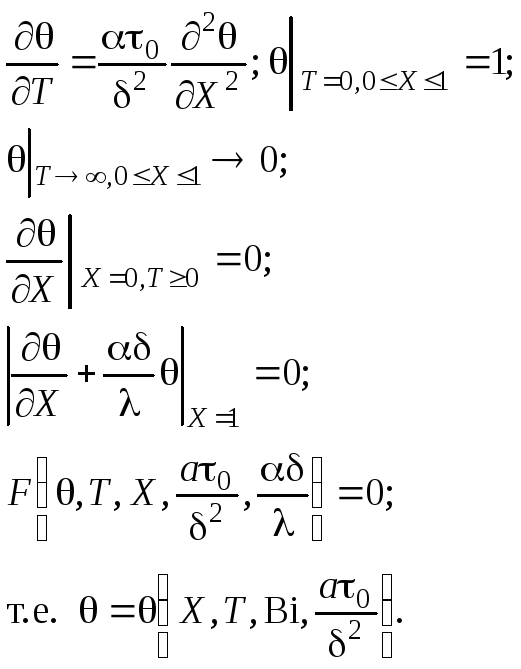
Однако данное решение не может зависеть от масштаба времени ₀, который не входит в математическое описание процесса, т.е. величины, содержащие ₀, должны находиться в сочетании, когда ₀ сокращается; другими словами, в виде произведения: получим: .

Достоинства метода:

1) возможность получения точно таких же безразмерных величин, которые вытекают из аналитического решения;

2) наглядность получения безразмерных величин - виден источник их происхождения (например, Вi из граничных условий 3-го рода; Fо из дифференциального уравнения).

Недостатки метода:

1) необходимо располагать системой дифференциальных уравнений, описывающих процесс;

2) решение сложных задач требует громоздких выкладок и занимает много времени.

Пример 2. Для задачи (пример 1) используем метод анализа размерностей физических величин. Для этого достаточно располагать системой величин, которые определяют изучаемый процесс.

Для нагрева пластины имеем следующую систему связанных между собой величин:

.

1. Запишем единицы измерения всех размерных величин:

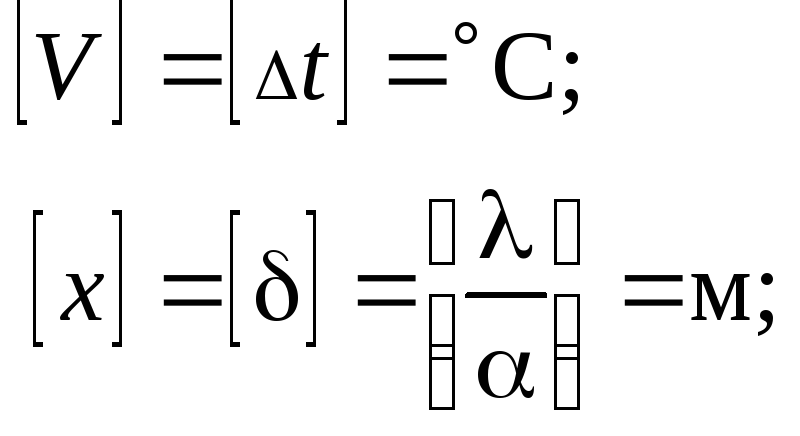
[] = с;

[a] = м²/с.

Перейдем к новым независимым единицам измерения:

м' = м/A_e;

с' = с/A_;

град' = С/A_t.

Пока коэффициенты А численно не определены.

2. Группируем их.

3. Выделяем группы с независимыми размерностями.

4. Переходим к новым единицам измерения, связанным с независимыми размерностями.

5. Переписываем функцию в новых единицах измерения:

.

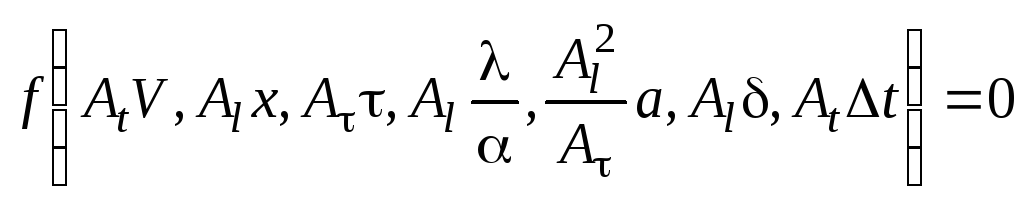Процесс не зависит от размера единиц, которые были использованы для измерения величин. Поэтому уравнение должно сохранить свою структуру, какими бы ни выбирались коэффициенты А.

Выберем их так, чтобы в уравнении осталось минимальное количество членов:

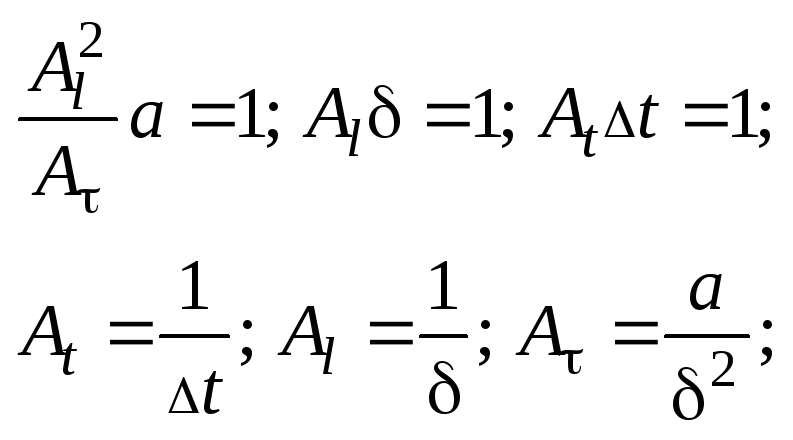
Рис.4.1.

или -

в этом уравнении неизвестен характер связи между величинами. Поэтому поищем эту связь в виде степенной зависимости:

.

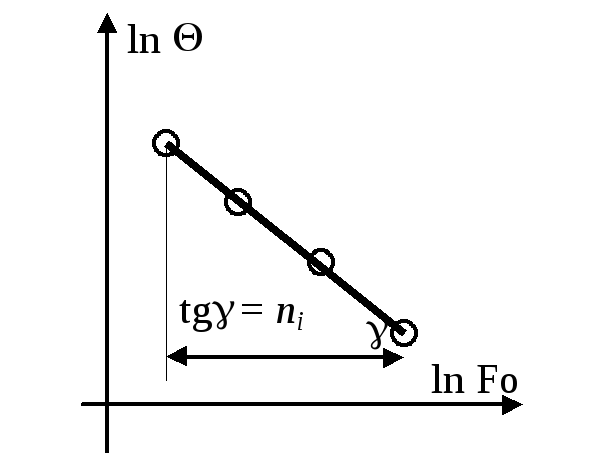
Экспериментальные данные при Bi = const и X = const обработаем в логарифмической сетке , тогда , или , т.е. n₁ является tg угла наклона кривой в логарифмических координатах (рис.4.1). После расчета n₁ находим аналогичным образом n₂ и n₃. Затем по любой точке на кривой находим значение константы С. Таким образом получаем полуэмпирическую инженерную расчетную зависимость.

Достоинства метода: при исследовании малоизвестных явлений, для которых дифференциальные уравнения еще не составлены, метод размерностей - единственный способ получения безразмерных величин, а также полуэмпирических расчетных обобщающих зависимостей. При этом используется теория подобия и эксперимент.

Контрольные вопросы

1. Получить безразмерную зависимость для нестационарной теплопроводности в тонкой пластине с использованием метода анализа размерностей для зависимости .

2. В чем суть метода преобразования масштабов и его отличие от метода анализа размерностей?

Общие контрольные вопросы и задачи к главе 4

1. В чем заключаются особенности методик получения зависимости тепловой нагрузки тонкой пластины от температурного напора и ее термического сопротивления с использованием уравнения Фурье и метода анализа размерностей (получить двумя этими путями эту зависимость)?

2. Как используется аксиома теории подобия в приведении зависимостей к безразмерному виду?

3. Написать порядок расчета при выполнении простейшей модели длинного охлаждаемого или нагреваемого тонкого подложкодержателя для обеспечения полного подобия процесса нестационарной теплопроводности.

Задача 1. Используя метод анализа размерностей для приведения зависимости к безразмерному виду, получить зависимость плотности теплового потока q от определяющих ее величин для плоской пластины в случае стационарного режима.

Ответ: .

Задача 2. Получить зависимость скорости свободного падения тела в вакууме W от высоты h и ускорения свободного падения q, проведя анализ размерностей для зависимости .

Ответ: .

48