Глава 7 Теплообмен при естественной конвекции § 7.1. Исходная система определяющих параметров

Естественная конвекция в большом объеме определяется _ - температурным коэффициентом плотности [град^-1], который рассчитывается из зависимости .

Рассмотрим, как и при вынужденной конвекции, систему определяющих параметров: , которая после приведения к безразмерному виду методом анализа размерностей получает вид

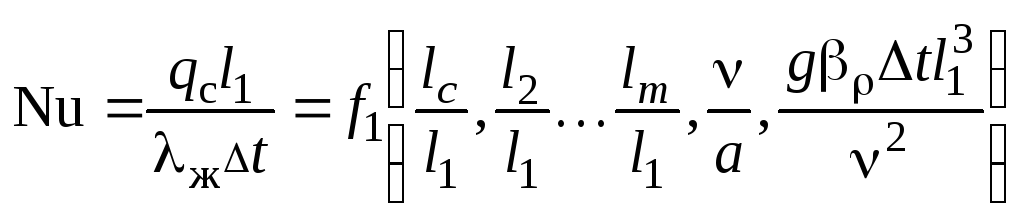= f₁(L_i, Pr, Gr),

где - число Грасгофа.

Физический смысл числа Грасгофа: мера отношения подъемных сил к силам вязкости.

§ 7.2. Критерий перехода ламинарного режима в турбулентный

К

Рис.7.1.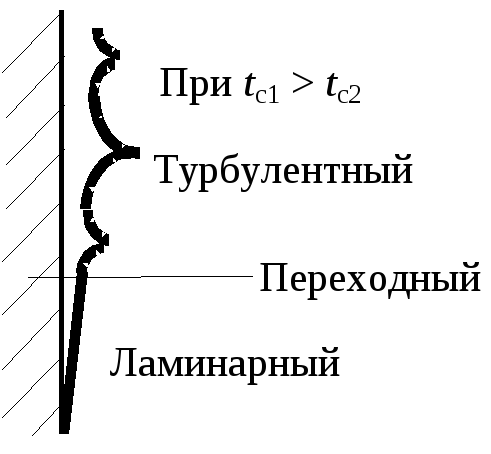

ак и при вынужденной конвекции, при естественной конвекции наблюдаются три режима течения (рис.7.1): ламинарный, турбулентный и переходный. Однако переход из одного режима в другой определяется числом Релея: Ra = GrPr, причем переходный режим при 10⁹ < Gr·Pr < 810¹⁰

,

где g = 9,81 м/c².

§ 7.3. Теплоотдача у вертикальной стены

Этот случай определяется следующим видом расчетной зависимости:

или

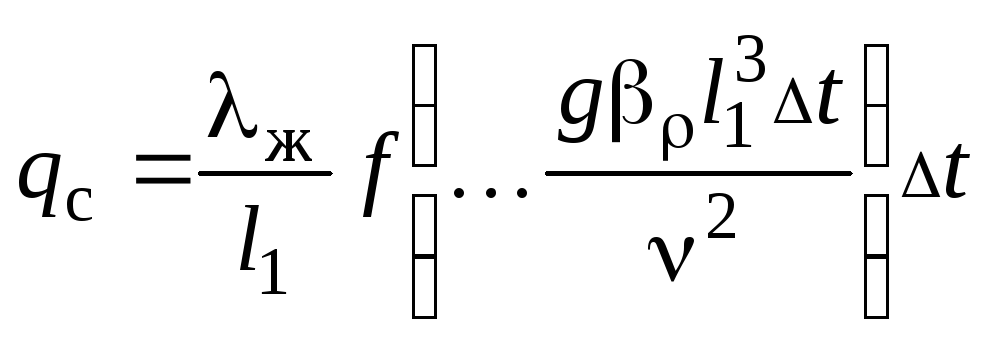, т.е. ,

таким образом, закон Ньютона - Рихмана при естественной конвекции не выполняется, поскольку коэффициент теплоотдачи зависит от t.

П

Рис.7.2.

оведение локального коэффициента теплоотдачи с изменением высоты h подчиняется следующей зависимости: в ламинарном режиме  падает, затем в зоне переходного резко возрастает, а в турбулентном остается постоянным. Это объясняется поведением пограничного гидродинамического слоя (рис.7.2).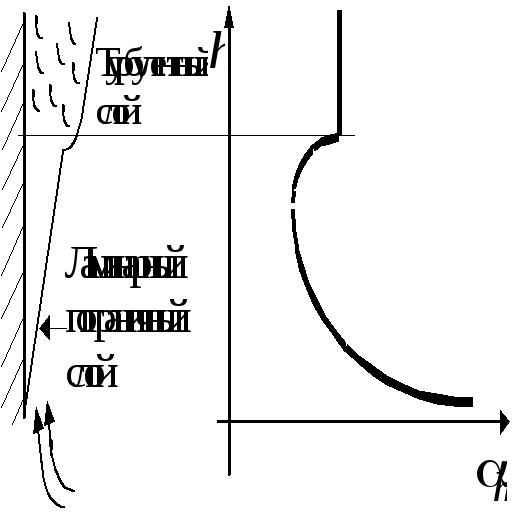

Контрольные вопросы

1. Получить методом анализа размерностей безразмерную зависимость для конвективного теплообмена при естественной конвекции (в общем виде).

2. Чем вызвано, что переход от ламинарного режима течения к турбулентному при вынужденной и естественной конвекции определяется различными критериями?

§ 7.4. Расчетные зависимости для конкретных задач естественной конвекции Задача 1. Вертикальная плоская стенка.

1

Таблица 7.1

Pr	0,73	10	100	1000
A	0,517	0,612	0,652	0,653

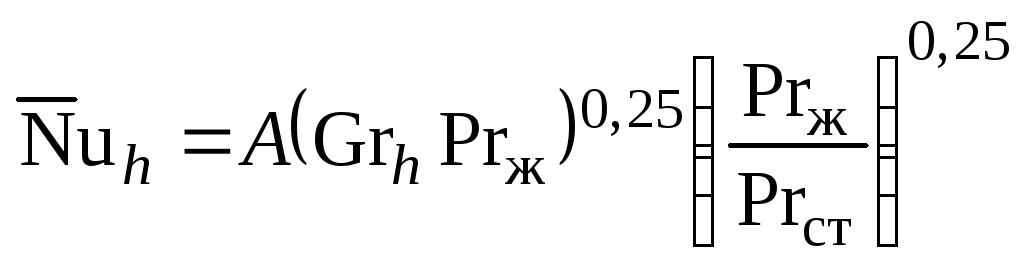. Ламинарный режим: , где коэффициент A зависит от числа Прандля и определяется по табл.7.1.

2. Турбулентный режим: 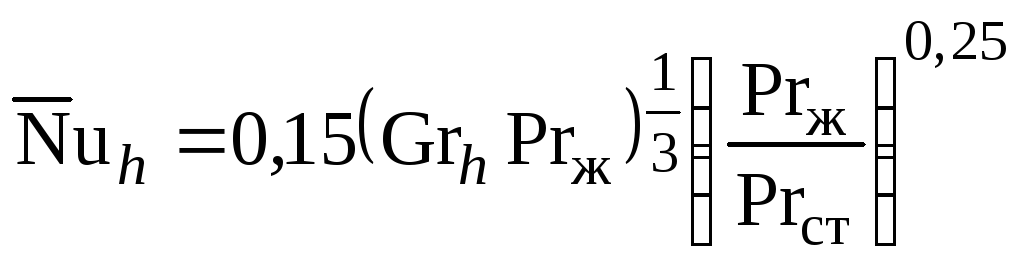, т.е.  не зависит от линейных размеров (см. рис.7.2), так как показатель степени равен 1/3, после преобразований получим

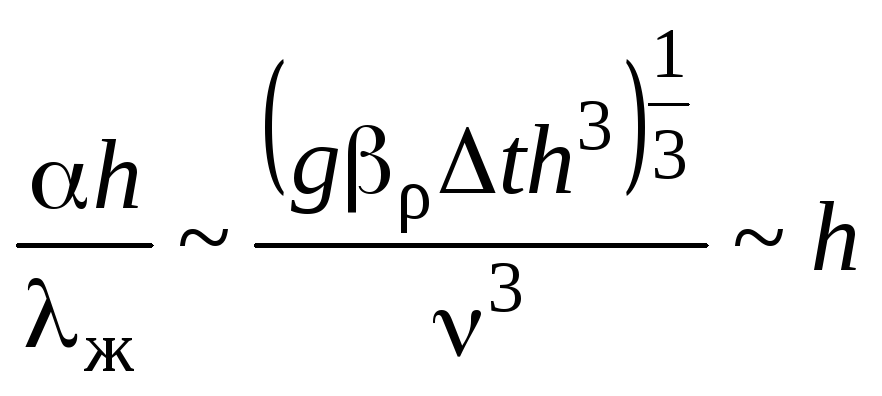, т.е. .

Задача 2. Предельные случаи теплообмена при естественной конвекции.

1. Силы инерции много меньше суммы подъемных сил и силы вязкости:

.

2. Силы вязкости много меньше суммы сил инерции и подъемных сил:

.

3. Конвективный перенос тепла много меньше переноса тепла теплопроводностью:

.

Для шара при GrPr  10³ расчетная формула вырождается в формулу Nu = 2.

Д

Рис.7.3.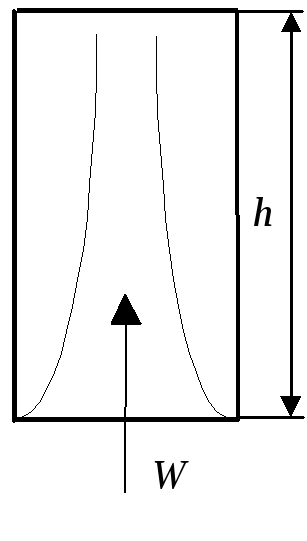

ля цилиндра при этих же значениях произведения GrPr расчетная формула имеет вид Nu = 0,5, т.е. расчетные формулы вырождаются в численные значения критерия Нуссельта.

Задача 3. Вертикальная труба, ламинарный режим:

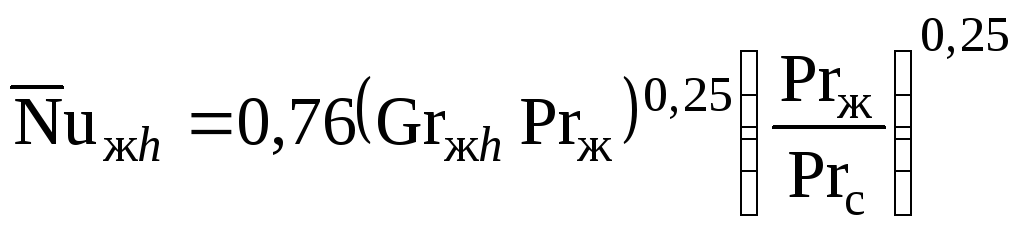
для , где определяющим размером является высота h (рис.7.3).

Задача 4. Горизонтальная труба, ламинарный режим:

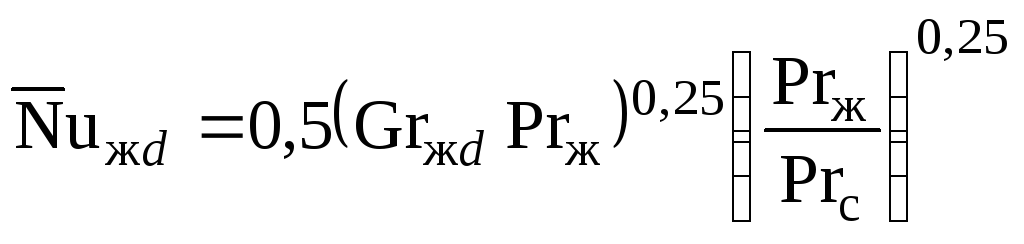
для , где определяющим размером является внутренний диаметр трубы d.

Задача 5. Вертикальная труба, турбулентный режим:

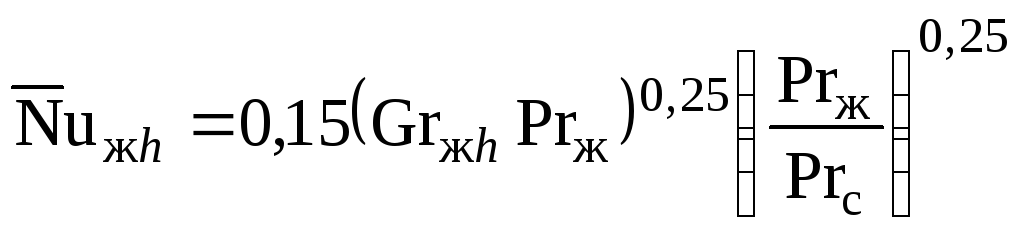
для , где определяющим размером является высота h. Таким образом, похожие зависимости для расчета коэффициента теплоотдачи  для естественной конвекции могут быть применены к случаям: вертикальная стена, цилиндр и горизонтальная труба. Внутри горизонтальной трубы характерным размером становится внутренний диаметр трубы, так как в его пределах развивается естественная конвекция.

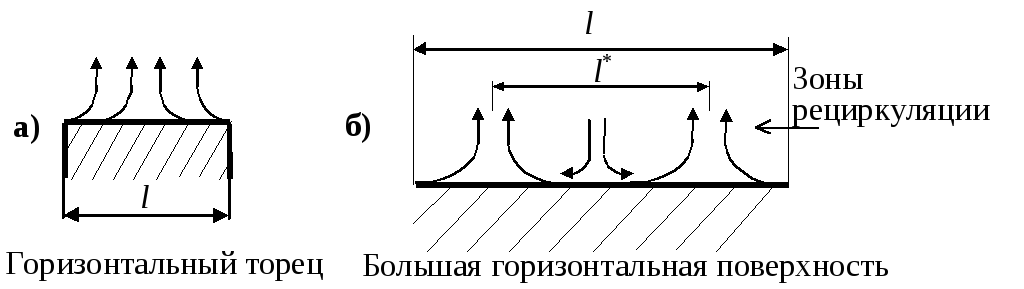
Задача 6. Естественная конвекция у горизонтальной поверхности, ламинарный режим.

Если l/2 < h_кр, рассчитанной из Ra_кр = 10⁹, то для геометрических случаев, показанных на рис.7.4, при t_ж > t_c  рассчитывается по l, у

Рис.7.5.

величенной на 30 % по сравнению с расчетной. Если поверхность теплообмена обращена вниз, как показано на рис.7.5, и температура t_c < t_ж при относительно малом размере l, то  рассчитывается по определяющему размеру l и уменьшается на 30 %.

К

Рис.7.4.

онтрольные вопросы

1. Обосновать, какой из вариантов расположения цилиндрических токовводов (горизонтальный или вертикальный) предпочтительней при их охлаждении свободным потоком воздуха. Оценку произвести для токовводов диаметром 5 и 10 мм.

2. Особенности гидродинамики и теплообмена при поперечном обтекании цилиндрических тел в случаях свободной и вынужденной конвекции.

3. Обосновать, какое расположение плоских тонких шин (токовводов) предпочтительнее - горизонтальное на широкой стороне, горизонтальное на узкой стороне (ребре) или вертикальное. Шина охлаждается только естественной конвекцией воздуха.

4. Объяснить, почему в случае турбулентного режима естественной конвекции на вертикальной поверхности (в отличие от вынужденной) локальный коэффициент теплоотдачи не меняется с высотой.

Задача 7.1.1. Рассчитать мощность, отдаваемую горизонтальным цилиндрическим реактором длиной 1500 мм и диаметром 400 мм, если реактор охлаждается естественной конвекцией: а) воздухом с температурой 200 С; б) водой с температурой 100 С.

Ответ: при охлаждении воздухом и водой мощность равна Q₁ = 2 кВт, Q₂ = 123 кВт.

Указания к решению:

.

а) .

10⁹ < Ra < 610¹⁰;

Ra = 1,19  10⁹, так как _ж = [ 1 – (t _ж – t) ];

₂₀₀ = ₂₀[ 1 – (200 – 20) ],

следовательно,

;

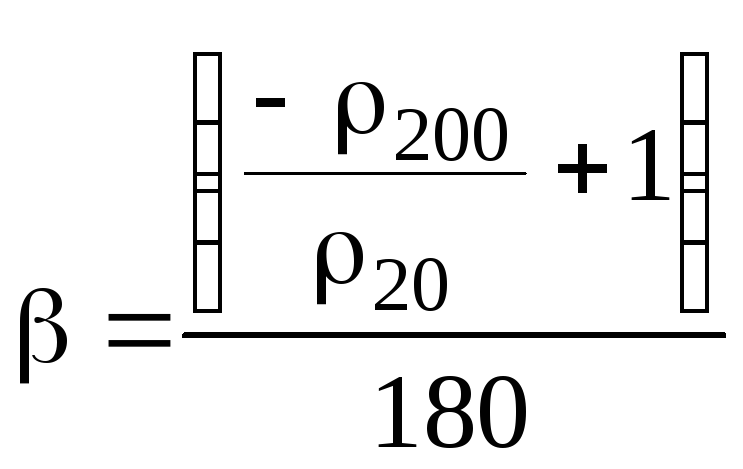для воздуха .

Режим ламинарный.

;

, следовательно, ;

;

б) .

;

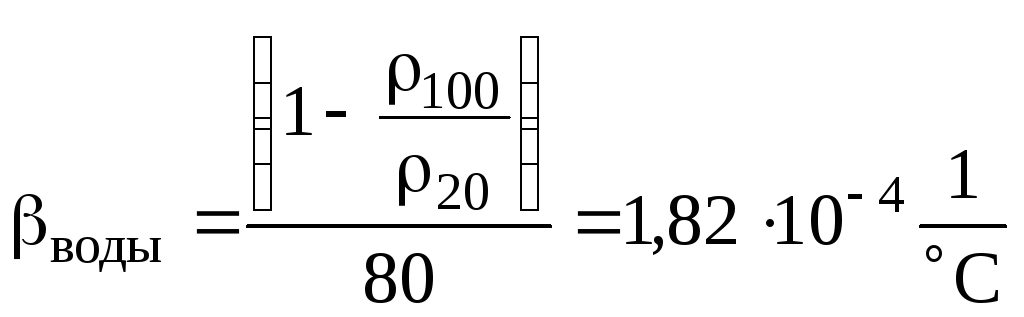Ra = 6  10¹⁰ ;

;

_лам рассчитывается аналогично а), однако вместо характерного размера берется 0,1.

Считаем _тур:

;

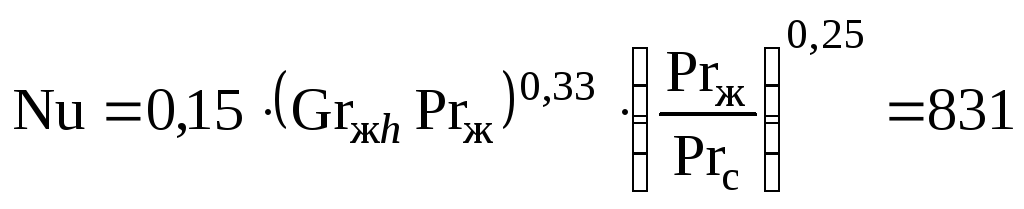; Q = 123 кВт.

Задача 7.1.2. Получить расчетную зависимость для теплообмена при естественной конвекции в виде безразмерной зависимости анализом размерностей.

Ответ: Nu = CGrⁿPr^kL_i^Pi.

Указания к решению: составить список определяющих параметров в виде функции

и выполнить анализ размерностей аналогично задаче 4.2.2.

Задача 7.1.3. Рассчитать потери тепла от горизонтального цилиндрического реактора (кожуха печи) длиной L = 1,5 м, диаметром D = 0,4 м, если реактор охлаждается естественной конвекцией: а) в воздухе ,; б) в воде , .

Ответ: потери тепла составляют Q  4  10³ Вт.

Указания к решению: свести данный геометрический случай к случаю вертикальной поверхности, где H = D. Определить режим течения по числу Ra:

.

Так как при этом значении Ra наступает турбулентный режим (граничное значение Ra = 10⁹), то определяется h_кр, при котором будет существовать ламинарный режим. Для этой зоны расчет ведется по формуле:

.

В результате получаем на ламинарном участке:

;

.

Для турбулентного участка, где H  h_кр, расчет выполняется по формуле:

.

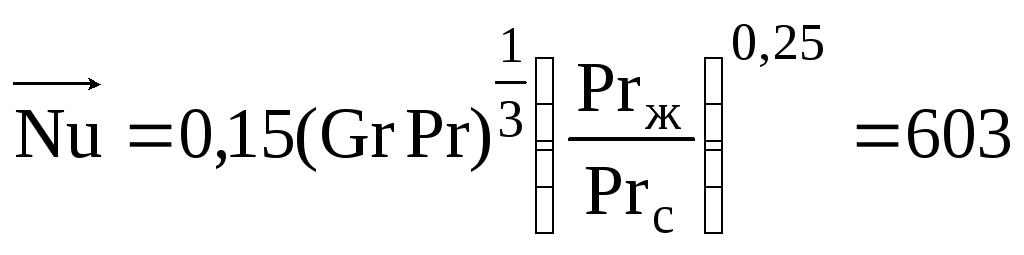Получаем на турбулентном участке:

.

Тогда суммарные потери будут равны:

.

Задача 7.1.4. Рассчитать градуировку термоанемометра расхода газа для следующих условий: 1) диапазон расхода газа G₁  G₂ 1 ‑ 10 л/мин; 2) температура газа t₂ = 20 C; 3) температура нити t_н = 300 С; 4) геометрические характеристики нити: d = 100 мкм, l = 20 мм; 5) диаметр камеры D = 50 мм; 6) используемые газы: аргон, кислород, водород, азот, воздух.

Ответ: .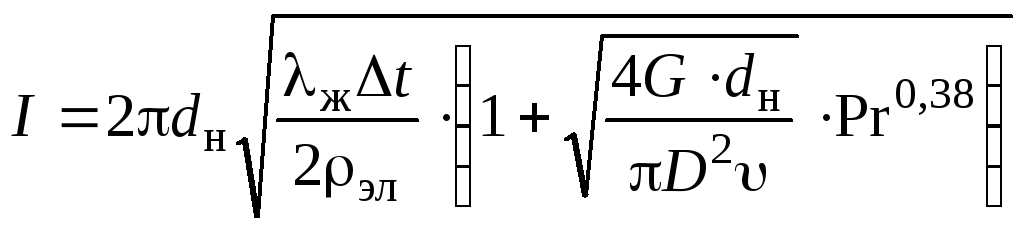

Указания к решению: необходимо установить зави­си­мость I = f(G).

.

Т

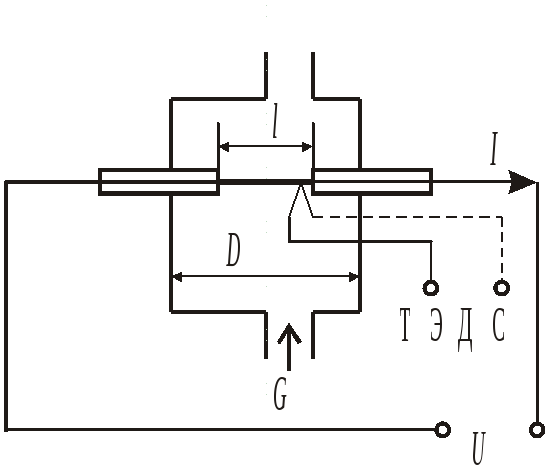Схема термоанемометра

ак как длина нити значительно больше ее диаметра, а температура нагрева не превышает 300 С, то потерями через теплопроводность и лучистый теплообмен можно пренебречь и считать, что охлаждение нити целиком зависит от естественной и вынужденной конвекции:

.

При естественной конвекции

;

так как число Ra мало, Nu = 0,5;

.

При вынужденной конвекции

;

.

Подстановка в уравнение

дает окончательную зависимость

.
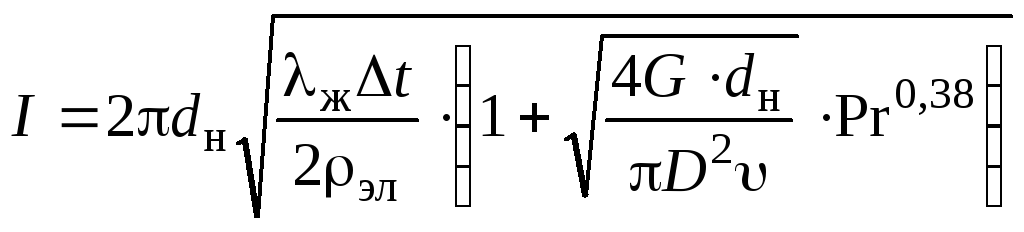