
- •Глава 3 Простейшие нестационарные процессы теплопроводности § 3.1. Нестационарный процесс теплопроводности в тонкой пластине и длинном цилиндре для граничных условий 3-го рода
- •Контрольные вопросы
- •§ 3.2. Нестационарный процесс теплопроводности в сложных телах, образованных пересечением простых тел
- •§ 3.3. Применение регулярного теплового режима для определения характеристик теплообмена
- •Контрольные вопросы
- •Общие контрольные вопросы к главе 3
Глава 3 Простейшие нестационарные процессы теплопроводности § 3.1. Нестационарный процесс теплопроводности в тонкой пластине и длинном цилиндре для граничных условий 3-го рода
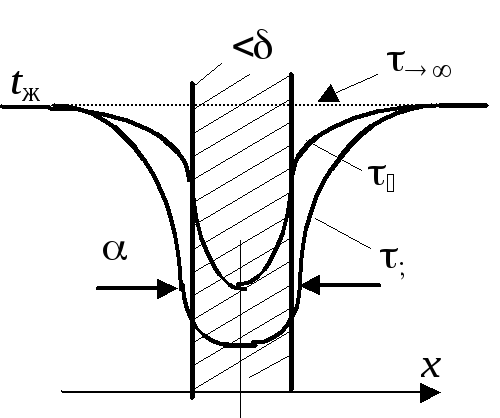
Задача. Определить нестационарное поле температуры в тонкой пластине, которая имела температуруt0, а затем в начальный момент времени0была помещена в жидкость сtж >t0(рис.3.1).
Задано: , a, , , tж, t0 = const; qv = 0.
Найти: t = t(x, , , , a, , tж, t0).
Рис.3.1.
![]() [м2/с].
[м2/с].
Исходное уравнение преобразуется:
![]() ;
;
![]() ;
;
![]() ,
,![]() .
.
Временные условия:![]() ,
,![]() .
.
Граничные условия:![]() .
.
Условие симметрии:![]() .
.
Введем V = tж-t, тогда уравнение с граничными и временными условиями примет вид
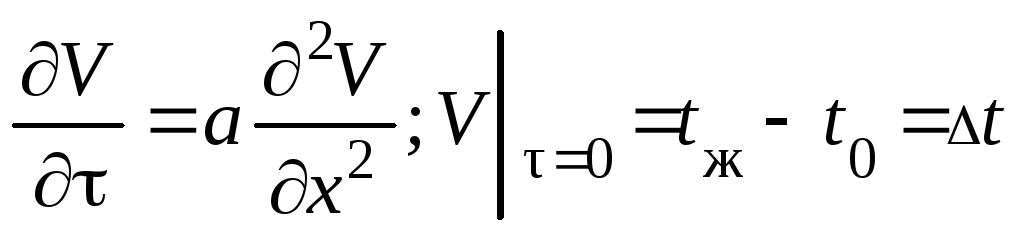 ;
;
![]() .
.
Решаем методом разделения переменных:
![]() ,
,
в результате уравнение примет вид
![]() или
или![]() .
.
Решая получившиеся два уравнения:
![]() и
и![]() и используя условие
и используя условие![]() ,
условие симметрии и граничное
условие
3-го рода, получаем решение в виде
,
условие симметрии и граничное
условие
3-го рода, получаем решение в виде
![]() ,
,
где nkнаходим из уравнения![]() ,
вытекающего из граничного условия, аС5- из временного условия.
,
вытекающего из граничного условия, аС5- из временного условия.
Таким образом, данная задача имеет
множество решений, так как получаемое
решение есть частное решение (рис.3.2)
трансцедентного уравнения
![]() .
Общее же решение можно представить
суммой всех частных решений:
.
Общее же решение можно представить
суммой всех частных решений:![]() ,
что в конечном счете дает
,
что в конечном счете дает
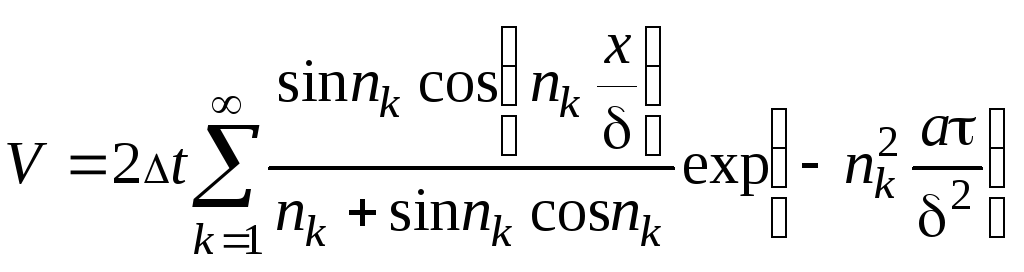
Рис.3.2.
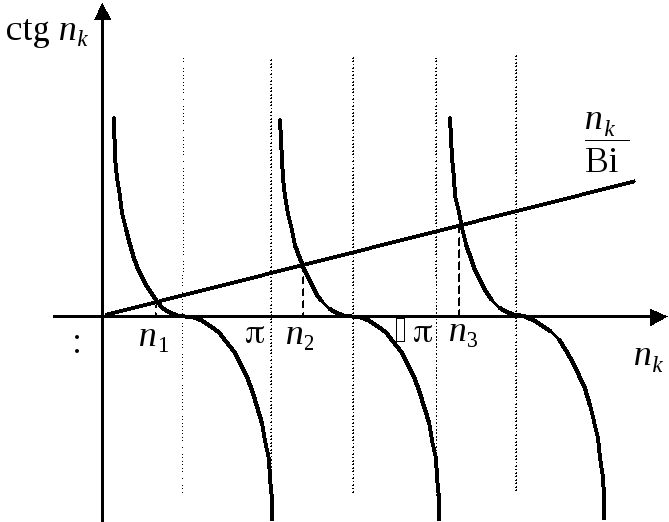
![]() ,
где
,
где![]() ;
;![]() ;
;![]() (число Фурье).
(число Фурье).
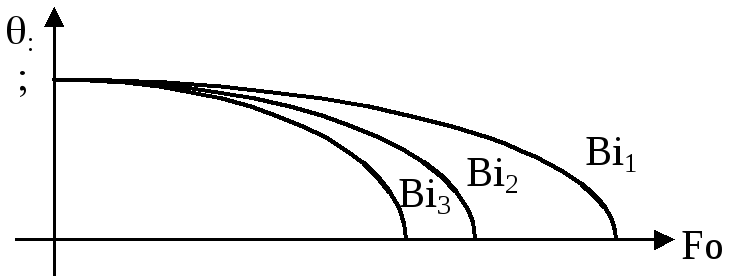
Рис.3.3.
 расчетном
уравнении нестационарной теплопроводности,
которое связывает четыре безразмерных
величины вместо восьми размерных:
расчетном
уравнении нестационарной теплопроводности,
которое связывает четыре безразмерных
величины вместо восьми размерных:
![]() ,
,![]() .
.
Во многих практических расчетах необходимо определить:
1) либо температуру на поверхности пластины
![]() ;
;
2) либо температуру в центре пластины
![]() .
.
Пользуясь графиком 0и1, можно выполнить расчеты трех типов.
1. Заданы: продолжительность нагревания (охлаждения) пластины, т.е. число Fо, и интенсивность теплоотдачи на ее поверхности, т.е. число Bi.
Определить: температуру на поверхности и в центре0и1.
2. Заданы: температуры1или0и число Bi.
Определить: продолжительность нагрева (охлаждения) до этих температур, т.е. число Fо.
3. Заданы: продолжительность нагрева (охлаждения, т.е. число Fо) до температуры и1(или0).
Определить: потребную интенсивность теплоотдачи на поверхности пластины, т.е. число Bi.
Для бесконечно длинного цилиндра место
хзанимаетr:![]()
![]() , - то же, что и в
плоской пластине.
В справочной
литературе имеются аналогичные расчетные
номограммы1и0, конечно,
численно отличные от тонкой пластины.
, - то же, что и в
плоской пластине.
В справочной
литературе имеются аналогичные расчетные
номограммы1и0, конечно,
численно отличные от тонкой пластины.
Контрольные вопросы
1. Как рассчитать температуру в центре и на поверхности тонкого плоского подложкодержателя в различные моменты времени при его внесении в зону реактора с протоком горячего газа?
2. Как рассчитать температуру в центре и на поверхности длинного цилиндрического подложкодержателя в различные моменты времени при его охлаждении на воздухе после его извлечения его из реактора?
3. Объяснить физический смысл чисел Био и Фурье. Что дает их использование в нестационарной теплопроводности?
Задача 3.1.1.Лист резины толщиной 20 мм после обработки в автоклаве при температуреt0= 140С вынут на воздух. Температура воздухаtж= 15C.
Определить температуру в середине и на поверхности пластины через время 1= 20 мин после начала охлаждения. Коэффициент теплоотдачи= 65 Вт/м2C.
Ответ:![]() ;
;![]() .
.
Указания к решению:из справочника выбрать теплопроводность резины= 0,175 Вт/мC и коэффициент температуропроводностиa= 0,83310–7м2/с, рассчитать числа Bi, Fo и, по графикам для бесконечно длинной пластины:x = 0=f1(Bi, Fo) иx = 1=f2(Bi, Fo), найти безразмерные температуры, от которых перейти к истинным температурамtx = 0иtx = .
Задача 3.1.2.Стальной вал диаметромd= 120 мм помещен в закалочную печь с температуройtж= 820С. Определить время, необходимое для его нагрева. Нагрев считать законченным при температуреt= 800C.
Определить температуру на поверхности вала в конце нагрева.
Ответ: = 51 мм;tr = r0= 804C.
Указания к решению:коэффициенты
теплопроводности и температуропроводности
стали, взятые из справочника, равны= 21 Вт/мC,a= 6,110–6м2/с.
Аналогично задаче 3.1.1, но по графику для
бесконечно длинного цилиндраr = 0=f1(Bi,
Fo), исходя из безразмерной температуры
и числа Bi, найти число![]() .
Принять начальную температуруt0= 20С,
аr0= 0,5d. Из безразмерного
числа Фурье найти время,
после чего, используя другой графикr = r0=f2(Bi,
Fo), рассчитать температуру на поверхности.
.
Принять начальную температуруt0= 20С,
аr0= 0,5d. Из безразмерного
числа Фурье найти время,
после чего, используя другой графикr = r0=f2(Bi,
Fo), рассчитать температуру на поверхности.
