Лекция №16.

Э

мольные доли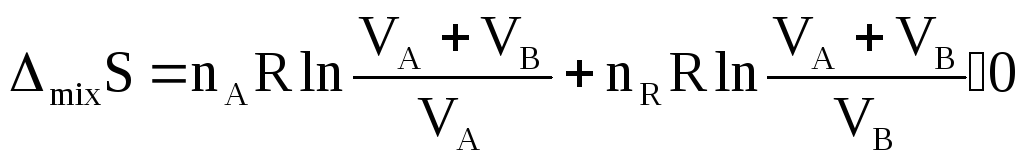

нтропия смешения:

Когда: p_A=p_B

∆_mixS=-R(n_AlnX_A+n_BlnX_B)0

Если 1 моль газа, то можно записать

∆_mixS=-R(X_AlnX_A+X_BlnX_B)0.

∆_mixS не зависит от природы смешиваемых газов, а зависит от их количества.

Докажем это утверждение:

S=nc_VlnT+nRlnV+S₀ – определяем энтропию системы, состоящей из двух газов, до смешивания и после смешивания.

Возьмем 1 моль газа А и 1 моль газа В

а) общий случай

Тогда энтропия исходной системы определится выражением

S

const интегрирования

_исх=S_А,исх+ S_В,исх=R(n_AlnV_A+n_BlnV_B)+(T)+S_AO+S_BO

т.к. изотермический процесс смешения

слагаемое c_VlnT обозначим через (Т)

S_кон=S_А,кон+S_В,кон=R(n_AlnV+n_BlnV)+(T)+S_A1O+S_B1O.

б) Пусть теперь n_A=n_B=1 моль если p_A=p_B V_A=V_B=V_o

S_исх=2RlnV_o S_1кон=2RlnV=2Rln2V_o

∆S_mix=S_кон-S_исх=2Rln2.

Следовательно при смешение газа энтропия не определяется природой, а определяется их количеством.

Если энтропия смешения не зависит от природного газа, то можно поставить опыт, когда в байде находиться однородный газ.

С физической точки зрения при смешение однородного газа ∆S=0, а по парадоксу Гиббса ∆mixS=2Rln2?

∆_mixS=-n_ARlnX_A-n_BRlnX_B – если газ однородный образовавшийся в системе после снятия перегородки (X_A=n_A/(n_A+ n_A), если однород. X_A=1).

С физической точки зрения при смешивание однородных газов энтропия не до. изменяется, т.к. при снятие перегородки в системе в системе с двумя порциями одного и гоже газа – никакого смешения не происходит. В чем ошибка, когда мы приходим к результату ∆S0, здесь мы сталкиваемся как будто с противоречием представляющим парадокс Гиббса: формулировка: энтропия смеси идеального газа равна сумме энтропий отдельных газов, когда каждый из них занимает весь объем.

Разрешение парадокса Гиббса: смешение двух идеальных газов нельзя рассматривать как предельный случай смешения двух различных газов; при переходе от …. Сколько угодно близких по свойствам газов, которые разделены в этой смеси, к смеси одинаковых газов энтропия смешения испытывает скачок – это и есть парадокс Гиббса. Разделить n_Тиб значит установить физическое значение скачка величины изменения энтропии при переходе от смеси сколько угодно близких газов к смеси одинаковых газов.

В литературе известна точка зрения (Вестхард, Шредингер, Кедров) – химические различия между газами непрерывной величиной, которая постепенно сходила бы на нет. Есть только два предельных случая: или различие существует или его совсем нет.

Физическим основанием П.Г. – невозможность разделения на первоначальные порции смеси тождественных газов (мы не можем разделить одинаковые газы на одинаковые порции).

В отличия термодинамика допускает разделение смеси сколь угодно мало отличающихся газов на отдельные части.

Смеси тождественных газов и отличие смеси разных газов при переходе от сколь угодно близких газов к смешиванию тождественных газов  ∆S.

Необратимые смешивания газов (при T=const).

Смоделируем процесс смешивания:

Система в термостате производим смешивание газов А и В убирая газа, потом произойдет самопроизвольное смешивание газа  процесс необратимый; т.к. T=const изменение внутренней энергии равно 0, газы идеальны,; на систему не действовали внешние силы  система не производит работы.

Q=∆U+A ∆U=0 A=0  Q=0,

т.е. процесс самопроизвольного смешивания при T=const не будет сопровождаться выделением или поглощением теплоты. Исходное состояние системы такое же, как при обратимом изотермическом процессе, поэтому для расчета энтропии можно воспользоваться ранее полученными формулами.

∆_mixS=-R(n_AlnX_A+ n_BlnX_B)0, т.к. X_А(В)1.

Энтропия термостата не изменится, а энтропия изолированной системы (прибор + термостат) увеличится вследствие протекания процесса

∆S_изол0.

Выводы: из уравнения (1) и (2) вытекает:

1. энтропия смешения не зависит от температуры, что учитывается при рассмотрении начала термодинамики.

2. смешение газов сопровождается ростом энтропии, т.е. смешение газов – самопроизвольный процесс, его движущая сила – увеличение энтропии, т.к. теплота при смешивании идеальных газов отсутствует.

Представление об аддитивности свойств.

Т.к. энтропия – аддитивное свойство; запишем энтропию газов до смешения и после смешения:

S_исх=S_1,исх+S_2,исх

S_кон=S_1,исх+S_2,исх+∆_mixS – конечное состояние можно определить еще так:

S_кон=S_1,кон+S_2,кон поэтому эти формулы наглядно показывают нам, чем энтропия идеальных газов отличается от других свойств например внутренний энергии и энтальпии.

Для внутренней энергии: U_исх=U_1,исх+U_2,исх.

U_кон=U_1,кон+U_2,кон ∆_mixU=0.

Адиабатическое смешивание газов.

Рассмотрим случай, когда смешивание газов происходит в приборе адиабатической оболочкой.

Если процесс смешивания проводится обратимо, то изменение энтропии должно быть равно 0. При адиабатическом смешивании каждый из газов испытывает расширение и его температура понижается, поэтому этот вклад в энтропию системы определяется слагаемым:

∆S=(n_A+n_B)c_pln(T₂/T₁)+(вклад связанный с увеличением)+∆_mixS=0.

(n_A+n_B)c_pln(T₂/T₁)0; ∆_mixS0; T₂>T₁.

Увеличение беспорядка в системе, связанного с процессом смешения газа компенсируется за счет менее интенсивного теплообмена, т.к. газы охлаждаются.

Расчет

Кристаллизация охлажденной жидкости оценить ∆S воды при кристаллизации при t^o=-10^oC.

Т.к. изменение энтропии не зависит от пути перехода от истинного состояния к конечному надо рассмотреть такой путь перехода по которому процесс может протекать через ряд обратимых стадий. Здесь мы рассматриваем замерзание воды меньше ее точки равновесного замерзания.

, но переход H₂O из переохлажденного жидкого состояния в твердое можно провести обратимо через следующие стадии:

1. обратимое нагревание воды от –10^оС до 0^оС.

H₂O(ж,t=-10^oC) H₂O(ж,0^оС).

2. обратимое замерзание H₂O при 0^оС.

H₂O(ж,t=0^oC) H₂O(лед,t=0^оС) - процесс изотермический

3. обратимое охлаждение льда от 0^оС до –10^оС.

H₂O(тв,t=0^oC) H₂O(тв,t=-10^оС).