Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский технологический университет "МИСиС"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лекции Анализ Данных

.pdf

Скачиваний:

Добавлен:

20.04.2015

Размер:

659 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Решение системы алгебраических уравнений:

yi = i , i - опред-ль матрицы, в к-й i-столбец заменен столбцом правой части.

=det A - обратная матрица к матрице А

AA−1 = A−1 A = E

	a			a ...			a							A11		A21
A =		a	11	a	12		a	1n			−1		1	A11		A21
						...		2n	,	A		=			A	A
						...			,	A		=
			21		22
					...										12	22
	...				...		ann

Aij = (−1)i+ j M ij

M ij - соответствующий минор матрицы А Минор – вычеркнутый i-столбец и j-строка.

ГЛАВА 4.

МЕТОДЫ РЕГУЛЯРИЗАЦИИ.

ПАРАГРАФ 1. КОРРЕКТНОСТЬ ПО АДАМАРУ.

Задача явл-ся корректно поставленной, если выполняются след. 3 условия:

1.решение существует;

2.решение единственно;

3.решение устойчиво.

Ay = f – линейное уравнение А – линейный оператор;

y – искомое решение;

f – заданная правая часть.

y и f принадлежат соответствующему Гильбертовому пространству.

Задача не корректно поставлена, если не выполняется хотя бы одно из перечисленных выше условий.

Система линейных алгебраических уравнений (СЛАУ)

4, y1 = y2 = 2

− 2 y + 3 y

нарушен 1-ый пункт.

− y1 + 2 y

= 3,

y1 = y2 = 3

+ 4 y

=15;

− 2 y1 + 3y2

= 4 - сис-ма недоопределена, нарушен 2-ой пункт.

2 y1

− 3y2

= 3,01

- сис-ма неустойчива

+ 2 y2 = −2

−1,33y1

= 2

≈ 0,5%

- т.е. изменяет правую часть.

= 0,33

	2 y1	− 3y2 = 3	y1 = 3
		+ 2 y2 = −1,99		=1
−1,33y1			y2

ПАРАГРАФ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.

При обработке результатов экспер-та Метод Наименьших Квадратов называют метод подбора праметров модели исхода из условия минимизации невязки.

Рассмотрим МНК в общем виде для систем ЛАУ:

Ay = f
a	a ...
11	12
A = a21	a22 ...
	...
...	...

a1n

a2n , m > n ,

amm

y1 y = M fyn

=Mfn

Учитывая, что сис-ма переопределена, то невозможно подобрать решение (наруш. 1 пункт) Ay − f ≠ 0

В методе наименьших квадратов условие невязки заменятеся на условно ее min.

Ay − f = min

Псевдо решение переопр-й СЛАУ явл-ся решение, удовлетворяющее условию минимизации невязки.

Условие минимизации невязки:

Ay − f = min Ù Ay − f 2 = min =>

??????????????????????????????????????????

Дифф-ем ( 1-ая производная д.б. = 0)

A* (Ay	− f ) = 0 - производная Фреше
a		a		,	a*		a*	строки на столбцы + комплексное сопряжение
A =	11		12	,	A* =	11	21	строки на столбцы + комплексное сопряжение
						*
a	21	L			a12

В случае если все элементы матрицы А дейстр. то совпадает с транспонир-й матрицей A* = АТ, где A* - сопряж-я, АТ – транспонир-я

A* Ay = A* f By =U ,

где B = A* A = AT A

U= A* f = AT f

Öпсевдо решение удовл.

Bij

= ∑aikT akj =

∑aki akj

k =1

Ui = ∑aikT fk = ∑aki fk

k =1

Пример:

2 y

− 3y

= −4,

2 − 3

− 4

Ay = f, By =U

− y1 + 2 y2 = 3, Ù

−1 2

3 ,

+ 4 y2

=15;

1 4

B11 = ∑Ak1 Ak1 = 4 +1 +1 = 6 =A11 A11 + A21 A21 + A31 A31

k =1

B22 = ∑Ak 2 Ak 2 = 9 + 4 +16 = 29 =A12 A12 + A22 A22 + A32 A32

k =1

B12 = ∑Ak1 Ak 2 =A11 A12 + A21 A22 + A31 A32 = −4

k =1

B21 = −4

6 − 4

− 4 29

U1 = ∑ak1 fk = a11 f1 + a21 f2 + a31 f3 = 2(−4) + (−1) 3 +15 = 4

k =1

U 2 = ∑ak 2 fk = a12 f1 + a22 f2 + a32 f3 = 78

k =1

Методом Крмера ищем решение полученной системы:

− 4

4 29 + 4 78

= 3,96 ,

y2 =

− 4

6 78 + 4 4

= 3,06

6 − 4

6 29 − 4 4

6 − 4

6 29 − 4 4

− 4

ПАРАГРАФ 3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ПРИМЕНИТЕЛЬНО К УРЯМ РЕГРЕССИИ.

- заключается в поиске коэф-тов регрессии исходя из минимизации невязки.

Рассмотрим ур-я регрессии 1-го порядка, а потом обобщим выкладки для общего порядка.

Y =b0 + b1 x

	X	Y
1	X1	Y1
2	X2	Y2
…	…	…
N	Xn	Yn

yi = yрасч.i − yэксп.i

∑ yi2

= min - остаточная сумма квадратов.

i=1

S = ∑ yi2

= min ∑( yi

− yPi )2 = min ∑( yi − b0

− b1 xi )2 = min

i=1

∂S

= 0

∑( yi −b0 −bn xi ) = 0

b0 n

+b1 ∑xi = ∑yi

∂b0

i=1

∂S

= 0

∑xi ( yi −b0

−b1 xi ) = 0

∑xi +b1 ∑xi2 = ∑xi yi

∂b

i=1

∑yi

∑xi

∑xi yi

∑xi2

b0 =

(∑yi )(∑xi2 ) − (∑xi yi )

∑xi

∑xi2

n∑xi2 −

(∑xi )2

ni ∑xi yi − (∑xi )(∑yi )

∑yi

∑xi

∑xi yi

(∑xi )

b =

n∑xi −

∑xi

∑

∑ i

y =b

+ b x + b x2

b0 + b1 ∑xi + b2 ∑xi2 = ∑yi

∑xi2 + b2

∑xi3 = ∑xi yi

b0 ∑xi + b1

b0 ∑xi2 + b1

∑xi3 + b2

∑xi4 = ∑xi2 yi

Оценим погрешность коэф-тов регрессии:

y = b0

+ b1 x

b1 =

= ∑yi (xi −

)

n S x

i=1

∑(xi − x)

S x

i=1

b0 =

= ∑yi (z − xi x)

n S2

i=1

z =

∑xi

i=1

Будем считать что х задается точно, а дисперсия у равна σ y2 . Посчитаем дисперсию коэф-та регрессии:

− b

)

= b

− b

∑

(z − xx)

−

x ∑

(z − x

σb2 =

nρx2

Коэф-т регрессии b0 b1 коррелированы

σ y2

−

Kb b

=... =

σb σb

nρx2σb

σb

0 1

Оценим погрешность у расч.: y p = b0 + b1 x

σ 2

−

02 + 2

x +

12 x2

−

02 − 2

x −

12 x2

+ b x)

b b

y p

0 1

σb2

+σb2 x 2 + 2x Kb

σb

σ y2

[(x −

+ ρa2 ]

nρx2

Замечание 1: Точность коэф-тов регрессии тем выше, чем больше δx , т.е. чем больше разброс точек вдоль оси х.

Замечание 2: Точность кэф-тов регрессии b0 тем выше, чем меньше x . Замечание 3: Точность урасч. Максимально в окрестности xcp .

МЕТОДЫ ПСЕВДООБРАТНОЙ МАТРИЦЫ МУРА ПЕНРОУЗА. МПоМ.

МПоМ на примере СЛАУ:

+ a

+... + a

пускай число уравнений m

...

n < m => существует множ-во решений у. решение не

единственно.

+... + a

Ay = f,

A =

y = M

f = M

a21

ρn

МПоМ позволяет выбрать «нормальное» решение этого уравнения

Нормальным решение ур-я наз-ся решение, имеющее минимальную норму ||y|| = min.

y = A+ f , A+ - псевдообратная матрица

Псевдообратной матрицей А наз-ся матрица A+ , к-я удовлетворяет след. условиям:

1)AA+ A = A;

2)A+ AA+ = A+ ;

3)(AA+ )* = AA+ ;

4)(A+ A)* = A+ A

A+ = lim[(αE + A* A)−1 A* ]

МПоМ МНК не гарантирует устойчивости решения

МНК И МПоМ ПРИМЕНИТЕЛЬНО К ИНТЕГРАЛЬНЫМ УРАВНЕНИЯМ ФРЕДГОЛЬМА I РОДА.

∫k(x, S) y(δ)dS = f (x)

x=[c, a]

δ=[a,b]

y(δ) - искомый спектр, входной. k(x, S) - ядро, ур-е Фредгольма

f(x) - заданная правая часть (измеренный спектр)

S - внутренняя переменная x - внешняя переменная

Ур-е Фредгольма I рода: ∫k(x, S) y(δ)dS = f (x), x [c, d ]

МЕТОД КВАДРАТУР (МЕТОД ТРАПЕЦИЙ)


1.	[a,b] разобьем с шагом			S = h1	= const ;
2.	[c,d] разобьем с шагом			x = h2	= const ;
3.	n =	b − a	+1 число узлов на h
3.	n =		+1 число узлов на h
		h1		1
		h1

m = d − c +1 число узлов на h2 h2

4. заменим интеграл на сумму, воспользовавшись формулой трапеции:

b	n
∫k(x, S) y(δ)dS ∑Py k(x, S y )y(S y )
a	y=1

S y = a + ( y −1)h1

h / 2, y =1, y = n
Py =	1	&	&
		&	&
	h1 , y ≠1,		y ≠ n

5.	вводим дискретизацию по х:
	xi = c + (i −1)h2
	n
6.	∑Py k(xi , S y ) y(S y ) = f (xi ), i =1/ m

y=1

∑Ai yy j = fi СЛАУ относительно yi

y=1

i= 1/m

Оператор – отображение одного пространства в другое Линейный оператор – оператор, который удовлетворяет след условиям:

1.x1 , x2 : A(x1 + x2 ) = A(x1 ) + A(x2 )

2.x1 , λ : A(λ2 ) +λA(x)

Теорема: Каждому лин-му оператору, действительной в лин-м пространстве размерности N, можно сопоставить квадратную матрицу размером (N,N); верно и обратное.

Обратимый оператор – оператор, который имеет обратный

Замечание: собственное значение обратимого оператора λi отличного от 0, собственное

значение обратного оператора = 1 .

λi

Оператор A* наз-ся сопряженным оператору А если выполняется след. соотношение: (Ax, y ) = (x, A* y)

Св-ва сопряженного оператора:

1)E* = E ;

2)(A + B)* = A* + B* ;

3)(A* )* = A;

4)(λA* ) = λA* ;

5)(AB)* = B* A* .

Оператор А наз-ся: самосопряженным, если A* = A Замечание: Оператор A* A явл-ся самосопряженным.

Док-во: (A* A)* = A* (A* )* = A* A

Св-ва самосопряженного оператора:

1)собственные значения самосопряженного оператора вещественны;

2)существует базис, в кот-м оператор А имеет простую структуру (матрица, соотв-ет лин. оператору, имеет диагональный вид)

Самосопряженный оператор А наз-ся положительным, если для x (Ax , x) ≥ 0

Св-ва:

1)собствен-е значения не отриц-ны;

2)A* A явл-ся положительным

(A* Ax , x) = (Ax , (A* )* x) = (Ax , Ax ) ≥ 0

Лиин. оператор А наз-ся ограниченным, если x N : Ax ≤ M x Нормой положит-го оператора явл-ся наименьшее собственное значение.

Теорема: Чтобы Ay = f была устойчива, необходимо и достаточно наличие обратного ограниченного оператор A−1 .

Есл лин. Оператор оператор А сим. Обратной A−1 , то A−1 тоже ограниченная

Для существования A−1 необх-мо и достаточно чтобы опер-р А был не вырожденным. Оператор А не вырожден, если определитель отличен от 0 ( верно и обратное).

ГЛАВА 5.

МЕТОДЫ РЕГУЛЯРИЗАЦИИ И АПРОКСИМАЦИИ.

ПАРАГРАФ 1. МЕТОД РЕГУЛЯРИЗАЦИИ ТИХОНОВА.

Явл-ся обобщение МНК и МПоМ.

Пусть имеется лин задача:

Ay = f

A A

− ~ ≤ξ

~	≤δ
f − f

~ = ~

Решаем задачу Ay f (приближенная задача) Далее «~» опускаем.

В методе регуляризации Тихонова одновременно условия минимаизации невязки и минимизации нормы. Т.о., минимиз. функционал.

Ay − f 2 +α y 2 = min

Ay − f - функционал Тихонова; α - параметр регуляризации (>0)

Дифференциальна функция:

A* ( Ay − f ) +αEy = 0
(A* A +αE) y = A* f	если α =0 невязка минимальна => МНК
y = ( A* A +αE)−1 A* f

Если α растет, невязка растет, решения были гладкими .

α надо подобрать так, чтобы обеспечить применим. Уровень гладкости и размер невязки. Если α →0 , => М…, решения становятся более гладкими.

Пускай B = A* A +αE, U = A* f By =U

Для того чтобы By =U , необходимо и достаточно наличие B −1 (огран)

Докажем наличие B −1 :

Собственное значение оператора В > 0, т.к. собственное значение A* A +αE > 0 => оператор В не рожден => det B ≠ 0 B −1 /

Докажем ограниченность B −1 . Нужно доказать, что В огранич. В положит-но, все значения положительны. Норма равна лин. значению => В огранич => B −1 огранич.

Выбор параметра α :

Для каждой задачи α подбирается индивидуально:

1)способ невязки

ξ= 0

из этих условий подбираем α .

Ay (α) − f =δ

α подбирается исходя из условий погрешности.

2)Пусть

= Ay −1

=(α)

Берем α, соответствующему значению min.

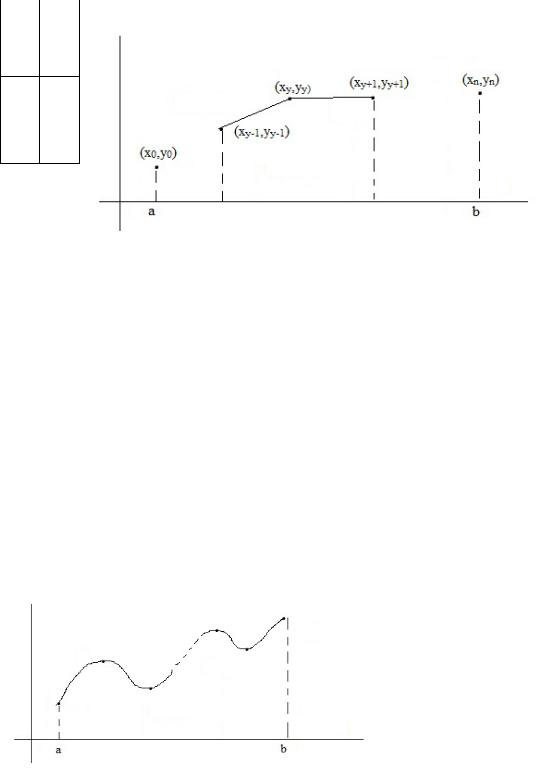
ПАРАГРАФ 2. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ.

Пусть имеется фун-я, заданная таблично:

X	Y	x0 < x1 <..., xy−1 < xy ... < xn
a=x0	y0	x0 < x1 <..., xy−1 < xy ... < xn
a=x0	y0	x располагаются по возрастанию.
x1	y1	x располагаются по возрастанию.
x1	y1
…	…
yy-1	yy-1
xy	yy
…	…
b=xn	yn

y(x) позволяет найти внутри диапазона ([a,b]). Рассмотрим способ задания

y(x) , к-й наз-

ся лин. интерполяция (экстраполяция).

Рассм-м [xy−1 , xy ]

, xy ] = kx

+ b

y[xy−1

) = y

y(x

=> находим a и b

~ y−1

y−1

y(xy ) = y y&

k =

y y

− y y−1

+ b = y y&−1

− xy&−1

kxy−1

kxy

+ b = y y&

xy y y−1 − xy−1 y y

b =

− xy−1

y &

− y

y−1

− x

y−1

x − x

y−1

y[x

y−1

, x

] =

x +

= y

y−1

y &

− xy−1

xy − xy−1

yy& - интерполяционная поправка.

Если ищем	~
	y(x) вне диапазона, то это экстраполяция, если внутри диапазона –

интерполяция.

ПАРАГРАФ 3. КВАДРАТИЧНАЯ ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ.

X	Y	a = x0 < x1... < xy <...xn = b
x0	y0	a = x0 < x1... < xy <...xn = b
x0	y0
…	…
xy-1	yy-1

xy&	y y&
xy+1	yy+1
…	…
xn	yn

Рассмотрим отрезок от xy−1 до xy&+1 . Проведем через точки кривую

+ β +γ (полином второй степени).

y(x) =αx

α, β,γ находятся из след сис-мы ур-й:

(xy−1 ) = y y−1

+ βxy−1

= y y−1

αxy−1

(xy ) = y y

+ βxy+γ

= yγ

αxy

) = y &

βxy+1 + γ = y y+1

y+1

αxy+1 +

y+1

Получим след-ю функцию:

(x − xy−1 )(x − xy+1 )

(x − xy )(x − xy−1 )

(x − xy )(x − xy+1 )

y &

y & +

y &

(x) =

(xy−1 − xy )(xy−1 − xy+1 )

(xy − xy−1 )(xy − xy+1 )

(xy+1 − xy )(xy+1 − xy−1 )

y−1

y+1

Если вычисленное значение у внутри отрезка, это интерполяция, вне – экстраполяция.

ПАРАГРАФ 4. ПОЛИНОМ ЛАГРАНЖА.

Пусть есть функция, к-я задана таблично, х удовлетворяет соотношению a = x0 < x1 <... < xn =b

полином степени n

~	n	+δn−1 x	n−1	+... +δ0
y(x) =δn x		+δn−1 x		+... +δ0

Константы находятся из условия:

~		) = y
y(x	0		0
~
y(xn ) = yn

~	n	n	(x − xi )
y(x) = ∑ ∏				y j
y(x) = ∑ ∏				y j
	y=0	i=0	(x j − xi )

Интерполяция (экстраполяция) хорошо работают если значения у не зашумлены.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.08.20191 Мб25Лекции - Введение в математическую логику №2.doc
#
01.07.202559 Кб1Лекции - конспект.docx
#
01.04.20252 Мб10лекции (первая часть).doc
#
01.03.2025984 Кб1лекции 5 сем. ст-ка.doc
#
01.04.20252 Мб2лекции А4 (вторая часть).doc
#
20.04.2015659 Кб43лекции Анализ Данных.pdf
#
16.11.2019246 Кб95лекции для заочного отделения.docx
#
01.04.2025838 Кб1Лекции Инвестиции(2013)Уч п.doc
#
01.07.20254 Мб1Лекции ИСиТ_заочное_2013+.doc
#
16.11.2018709 Кб20Лекции ИТвМ2011КОНТР_РАБ.doc
#
01.05.202513 Мб5Лекции КЭП СВТ.doc