лекции Анализ Данных

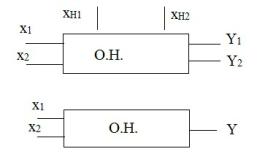
ПАРАГРАФ 1. Определение.

Планирование эксперимента – выбор числа и условия проведения опыта необходимо для решения заданных задач (с рассмотренной точностью)

Идея

Оптимальное управление эксперимента при неполном знании изучаемого объекта.

Необходимо:

1.min число опытов;

2.обеспечить варьирование всех параметров, от которых зависит объект;

3.действия экспериментатора формализовать.

Эксперимент бывает:

-пассивный: при котором экспериментатор не может управлять изучаемым объектом)

-активный: экспериментатор активно влияет на изучаемый объект.

ПАРАГРАФ 2. ОБЪЕКТ ИССЛЕДОВАНИЯ.

х1…х2 – управляемые параметры хН1…хН2 – неуправляемые параметры Y1…Y2 – свойства О.Н.

Эксперимент

-экстремальный: к-й ставится для решения задач оптимизации – оптимизация соотношений между факторами и свойством системы Поиск максимума и минимума

-интерполяционный: ставится для нахождения связи свойств объекта исследовании (ОИ) и входными параметрами .

ПАРАГРАФ 3. ПАРАМЕТР ОПТИМИЗАЦИИ.

Требование:

1.задан количественно;

2.однозначный (функциональная зависимость между Y и факторами);

3.существовать для мобильной комбинации значение которого могут принимать факторы;

4.универсальный (всесторонний характер О.Н.)

5.эффективный (определяется с max возможной для данных условий точностью).

ПАРАГРАФ 4. ФАКТОРЫ.

Требования:

1.задаваться количественно;

2.// - // - // область определения (совокупность всех знаний которые может принимать фактор)

3.управляемые (эксперимент может поддерживать фактор на заданном уровне сколько угодно);

4.Однозначность и независимость.

ПАРАГРАФ 5. МОДЕЛЬ.

Y = F (x1,...x2 ) описать изучаемый объект, либо написать функцию оптим.

Задать модель – выбрать вид функции оптимальных параметров, полученных на основе эксперимента.

Модель адекватна, если она позволяет предсказать свойства ОИ с требуемой точностью.

ПАРАГРАФ 6. КОДИРОВАНИЕ ФАКТОРОВ.

- все точки планируются вокруг т. xосн1

(Ii) Интервал варьирования - величина, добавление которой к основному уровню дает max значение, а а при вычитании min значение фактора.

xi = {xmax 1; xmax i }

Какие значения будет принимать кодированный фактор х1-? x1 = {−1,1}= {−;t}

ГЛАВА 2.

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА.

ПАРАГРАФ 1. ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ (ПФЭ)

- реализуются возможные комбинации

Уровни значения факторов.

Свойства полного факторного эксперимента:

N

1. симметричность ∑xij = 0

i =1

N

2. Ортогональность ∑xij xil = 0, l ≠ j

i=1

3. Нормировка ∑xij = N

i=1

F = b0 +b1x1 +... +bk xk

Функция оптим. в виде уравнения регрессии. Коэф-ты легко определить.

Y = b0 +b1xi +... +b2 x2

ПФЭ 22

N = mk = 22

x1 = {xmin ; xmax}

x1 = {xmin 2; xmax 2}

x2 = {−;+}

Изобразим область эксперимента в факторном пространстве.

Y =b0 + b1 x1 + b2 x2

σb1, 2 = σ2y - среднее квадратичное отклонение

Звучание, полный факторный эксперимент позволяет определить не только коэффициенты регрессии I порядка, но и коэф-ты уравнении, которые учитывают взаимодействие факторов.

ПАРАГРАФ 2. ДРОБНЫЕ ФАКТОРНЫЕ ЭКСПЕРИМЕНТЫ.

При увеличении числа факторов количество опытов растет по степенной зависимости. Если ограничиться линейной зависимостью, то число опытов можно сократить, используя дробно-факторный эксперимент (ДФЭ) (идея: мы принебрегаем эффектом взаимодействия факторов, вводим новый фактор)

Замечание №1: ДДФЭ отвечает всем свойствам ПФЭ (нормирование, симметрия, ортогональность);

Замечание №2: Если при ДФЭ реализ-ся половина ПФЭ, то ДФЭ обознач-ся 2k −1 , к – число факторов, 2 – число уровней, к-е может принимать фактор.

ПФЭ 22

Ур-е регрессии: Y =b0 + b1 x1 + b2 x2 + b12 x1 x2 Матрица регрессии (1)

Вводим нов x3

ПАРАГРАФ 3. ПЛАНИРОВАНИЕ II ПОРЯДКА.

Фун-ю отклика в области экстремума как правило удается описать ур-ем регрессии II порядка, вида Y =b0 + b1 x1 +... + bk xk + b11 x12 ...

Возможно использование центрального композиционного плана.

Построим:

Y =b0 + b1 x1 + b2 x2 + b12 x1 x2 + b11 x12 + b22 x22

Для того чтобы найти все коэф-ты уравнения необходимо чтобы каждому фактору приши 3 значения.

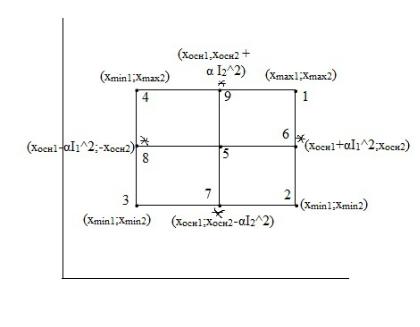
Матрица планирования не кодированных факторов.

Замечание №1: область которой соотв-ют опыты 1,2,3,4 наз-ся – ядром Замечание №2: постр. План не явл-ся ортогон-м

-скалярное произведение некот-х столбцов ≠ 0

-не может не завис. опред все коэф-ты ур-я регрессии!

Построим ортогон-й план (ортог-м постр план ЦХП)

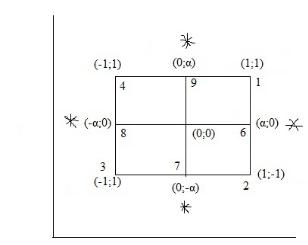
ПАРАГРАФ 4. ОРТОГОНАЛЬНЫЙ ПЛАН II ПОРЯДКА

Обработка результатов эксперимента.

Допустим, мы провели М парал-х опытов и получили такие результаты:

M : y(i) ; y(1) ...y( N )

Будем считать, что наиболее близкое к истинному среднее значение:

M

∑y(i)

y = i=1M

Абсолютная ошибка измерения – это величина, показывающее отклонение измер. величины от среднего значения

y (i) = y − yi

Для оценки погрешности измерений абс. ошибку использовать нельзя.

Среднее квадратичное отклонение (σ ) - величина, равная корню квадратному из дисперсии.

Дисперсия – ср. квадратичное отклонение случайной величины от его среднего.

M

∑ y (i)2

σ 2 = i=M1 −1

Виды ошибок:

Систематические ошибки – ошибки, связанные с неучтенными факторами при проведении эксперимента (будем считать что их нет).

Случайные ошибки – ошибки, зависящие от большого числа факторов, каждый из которых вносит небольшой вклад, к-й не явл-ся доминирующим.

Будем считать что истинное значение лежит в интервале [y −δ, y +δ] δ - доверительный интервал.

Вероятность того что мы попали в этот диапазон называется доверительным интервалом. Иногда исп-ют термин «уровень значимости» = 1 – доверит-ная вероятность.

δ =σ ttp,m - доверит-й интервал. t – коэф-т Стьюдента.

δ =σ ttp, f p = 0.95

F = M – 1 – число степеней свободы

ГРУБЫЕ ОШИБКИ.

При проведении эксперимента возможен брак, к-й приводит к грубым ошибкам. Эти результаты нужно исключить из обрат. Для этих целей исп-ют критерий Стьюдента, к-й заключается в след-м: ошибки явл-ся грубыми, если экспериментное значение коэф. Стьюдента больше табличного значения.

Пример: Пусть получены следующие значения.

[2,95]-? tp = 4,5 t0.95 , 3 = 4,3

2,40

2,60 y = 2,5

2,50

ОДНОРОДНОСТЬ СОВОКУПНОСТИ ДИСПЕРСИИ.

Дисперсии должны быть однородны. Для проверки однозначности пользуемся критерием Фишера, к-й заключ-ся в следующем: «Если экспериментальное значение Фишера превышает его табличное значение, то дисперсия явл-ся неоднородной» (большой разброс

взначениях дисперсии)».

σ2

σmax2 > Ff1 , f2 min

f1,f2 – число степеней свободы f1 = M1 -1 , f2 = M2 -1

ДИСПЕРСИЯ ВОСПРОИЗВОДИМОСТИ.

Оценивается дисперсии всего плана эксперимента, а не только одной строки.

Дисперсия воспроизводимости – дисперсия, полученная в рез-те усреднения опытов.

Для каждого вектор-строки имеет М опытов.

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

Основана на следующих постулатах:

-Значения, получившиеся в результате эксперимента, явл-ся случайными величинами с нормальным законом распределния;

-Значения факторов явл-ся не случайными величинами; точность задания фактора существенно превышает погрешность измерений, получаемых в результате проведения эксперимента;

-Дисперсия величин, полученных в эксперименте, не зависит от их абсолютных величин.

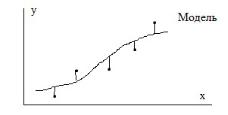
Мы провели серию опытов, на основе результатов строим кривую.

Величина, равная разнице между эксперимент-м значением и полученной по модели, назся невязкой.

Величина невязки, как правило, отличается от 0.

Причина невязки:

-ошибки при проведении опытов;

-непригодность модели;

ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ (часть 1)

Остаточная сумма квадратов – величина, равная сумме квадратов невязок.

Для оценки адекватности модели оценивают дисперсию адекватности:

f * - число степеней свободы;

yi - остаточная сумма квадратов.