Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov_Goryacheva_Rasputko

.pdf

Скачиваний:

Добавлен:

20.04.2015

Размер:

486.51 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Министерство образования и науки Российской Федерации Ульяновский государственный технический университет

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

ТИПОВОЙРАСЧЕТПОВЫСШЕЙМАТЕМАТИКЕ

СОСТАВИТЕЛИ: АНКИЛОВ А. В.

ГОРЯЧЕВА Н. Я. РАСПУТЬКО Т. Б.

Ульяновск 2004

УДК 519.2 (076) ББК 22.161 я7

Д 50

Рецензент – кандидат физико-математических наук, доцент кафедры математического анализа УлГПУ М. С. Чунаева.

Одобрено секцией методических пособий научно-методического совета университета.

Дифференциальное	исчисление функций	нескольких	переменных:
Д 50 типовой расчет по	высшей математике	/ Сост.: А.	В. Анкилов,

Н. Я. Горячева, Т. Б. Распутько. – Ульяновск: УлГТУ, 2004. – 32 с.

Настоящий типовой расчет составлен в соответствии с программами математических дисциплин для инженерно-технических специальностей вузов, утвержденных Главным учебно-методическим управлением высшего образования 7 июля 2000 года.

Изложена методика выполнения типового расчёта по теме «Дифференциальное исчисление функций нескольких переменных», приведены варианты типового расчета и даны образцы решения задач с предварительными пояснениями.

Работа выполнена на кафедре «Высшая математика» УлГТУ.

УДК 519.2 (076) ББК 22.161 я7

Учебное издание

Дифференциальное исчисление функций нескольких переменных

Типовой расчет по высшей математике

Составители: АНКИЛОВ Андрей Владимирович ГОРЯЧЕВА Наталья Яковлевна РАСПУТЬКО Татьяна Борисовна

Редактор Н.А. Евдокимова

Подписано в печать 10.06.2004. Формат 60×84/16. Бумага писчая. Усл. печ. л. 1,86. Уч.-изд. л. 1,87.

Тираж 450 экз. Заказ

Ульяновский государственный технический университет 432027, Ульяновск, ул. Северный Венец, 32.

Типография УлГТУ, 432027, Ульяновск, ул. Северный Венец, 32.

ОГЛАВЛЕНИЕ

Введение …………………………………………………………………….. 4

1.Теоретические вопросы ……………………………………………………. 4

2.Теоретические упражнения ………………………………………………... 5

3.Методические рекомендации к решению задач ………………………….. 6

4.Расчетные задания ………………………………………………………….. 20

Библиографический список .……………………………………………….. 32

-3-

ВВЕДЕНИЕ

Настоящий типовой расчет (ТР) предлагается студентам 1-го курса для более глубокого самостоятельного изучения темы «Дифференциальное исчисление функций нескольких переменных». Студент, выполняющий ТР, должен уметь правильно отвечать на теоретические вопросы, решать теоретические упражнения, а также решить задачи одного из вариантов (номер варианта указывается преподавателем). В четвертой части ТР даны методические указания и приведены образцы решения задач типового расчета.

1.ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ

1.Определение функций двух переменных, ее области определения. Геометрическое истолкование этих понятий. Понятие функции трех переменных.

2.Понятие предела функции двух и трех переменных в точке. Понятие непрерывной функции нескольких переменных.

3.Частные производные функции двух и трех переменных.

4.Определение функции, дифференцируемой в точке. Дифференциал первого порядка функции двух и трех переменных.

5.Уравнения касательной плоскости и нормали к поверхности.

6.Частные производные сложной функции нескольких независимых переменных. Полная производная.

7.Дифференцирование неявных функций одной и нескольких независимых переменных.

8.Определение частных производных высших порядков. Теорема о равенстве смешанных частных производных функции двух переменных. Дифференциал второго порядка функций двух и трех переменных.

9.Формула Тейлора и формула Маклорена для функции двух переменных.

10.Понятие точки экстремума функции двух и трех переменных.

11.Необходимые и достаточные условия экстремума функции двух переменных.

12.Необходимые и достаточные условия экстремума функции трех переменных.

13.Понятие точки условного экстремума функции двух переменных.

14.Необходимые и достаточные условия условного экстремума функции двух переменных. Метод множителей Лагранжа.

15.Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой ограниченной области. Теорема Вейерштрасса.

-4-

2. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ

1. Доказать, что если функция f (x, y) непрерывна в некоторой точке, то она непрерывна в этой точке и по каждой из переменных x и y в отдельности.

2. Доказать утверждение: если функция		f (x, y)	имеет	частную
производную f x′(x, y)	в некоторой окрестности	точки	M (a, b) ,	причем
существует предел lim	f x′(a + h, b)= c , то этот предел равен		f x′(a, b).
h→0

3.Температура Т воздуха в некоторой точке земной поверхности является функцией трех переменных: долготы точки λ, ее широты θ и момента времени t. Указать физический смысл частных производных Tλ′,Tθ′,Tt′.

4.Доказать утверждение: если функция f (x, y) удовлетворяет

неравенству | f (x, y) |< x2 + y 2 , то она дифференцируема в точке (0,0).

			x3 y
5. Доказать,	что	функция	f (x, y)= (x6 + y 2 ),			если		x6 + y 2 ≠ 0 , и
f (x, y) = 0 , если	x = y = 0 , – разрывна при			x = y = 0 ,			но	имеет частные
производные в точке (0, 0).			y			y
6. Доказать,	что	функция						удовлетворяет
			z = x g		+ y	g

			x			x

соотношению x2 z′xx′ + 2xyz′xy′ + y2 z′yy′ = 0 .

7.Доказать, что U ′y = g(z)U ′x , где U = f (z) , а z – функция от x и y, определяемая из уравнения z = x + y g(z) .

8.Доказать, что касательная плоскость к поверхности xyz = a3 в любой ее

точке образует с плоскостями координат тетраэдр постоянного объема. Найти этот объем.

9. Сумма нескольких положительных чисел, имеющих данное произведение, оказывается наименьшей тогда и только тогда, когда все эти числа равны между собой. Доказать.

10. Пользуясь определением, доказать, что функция z = x2 + y 4 имеет экстремум в точке (0,0).

11. Пользуясь определением, доказать, что функция U =sin 2 (x + y + z) имеет экстремум в точке (0,0).

12. Пользуясь определением, доказать, что функция z = x2 − y 2 в точке

(0,0) экстремума не имеет (причем точка (0,0) является стационарной для функции z).

13. Пользуясь определением, доказать, что функция z = x2 + y 2 в точке

(0,0) имеет экстремум. Доказать, что в точке (0,0) частные производные ∂z ∂x и∂z ∂y не существуют.

-5-

3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧ

ЗАДАЧА №1. Найти и изобразить на плоскости область определения

функции z =	ln	x2	+ y2	+ arcsin	y	+	x .
			4		x2
Решение.							функции z есть пересечение областей
	Область			определение

определения слагаемых функций. Первая функция: для того, чтобы квадратный корень имел вещественное значение, его подкоренное выражение должно быть

	x2	+ y 2
неотрицательным, т. е.	ln		≥ 0. Если значение логарифмической

		4

функции неотрицательно, то выражение, стоящее под знаком логарифма,

должно быть больше или равно единице, т. е. x2 +4 y 2 ≥1, отсюда x2 + y 2 ≥ 4 .

Это неравенство задает нам множество точек плоскости, лежащих вне окружности с центром в начале координат, радиуса 2, включая и точки данной

окружности. Вторая функция arcsin	y	определена при	−1 ≤	y	≤1, x ≠ 0 .
	x2			x2

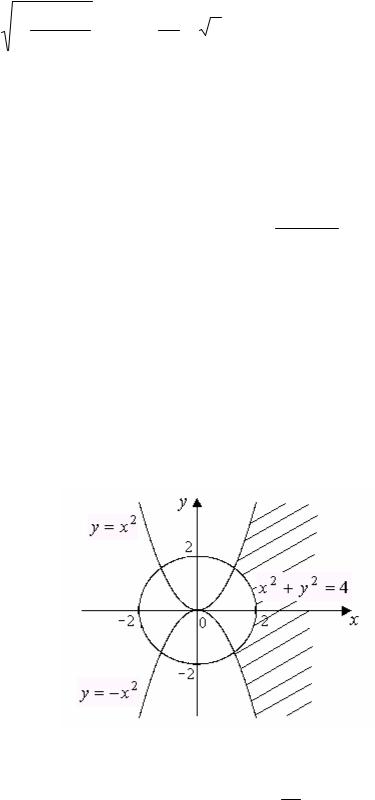
Следовательно, − x2 ≤ y ≤ x2 , x ≠ 0. Имеем две параболы с вершиной в начале координат y = x2 и y = −x2 . Поэтому полученное неравенство задает нам часть

плоскости, заключенную между этими параболами, включая границы без начала координат. Третья функция определена при x ≥ 0 .

Областью определения данной функции является общая часть найденных областей определения слагаемых (рис. 1).

Рис. 1. Область определения функции z(x,y)

ЗАДАЧА № 2.1. Найти производные сложной функции

z =ln(xy2 − 2x2 y) , где x = vu2 , y = u sin v .

Решение. Выполняя действия в соответствии с формулами:

z′	= z′ x′	+ z′	y′	,	z′	= z′	x′	+ z′	y′,
u	x u	y	u		v	x	v	y	v

-6-

zu′ =

y2 −4xy

2xy −2x2

получим:

sin v,

xy2 −2x2 y v2

xy2 −2x2 y

zv′

− 4xy

2xy − 2x2

−

u cosv .

xy2

− 2x2 y

xy2 − 2x2 y

Вместо x и y подставим их выражения через u и v. После несложных

преобразований получим:					2v2 sin v(v cos v −sin v)+8sin v − 2v cos v
zu′ =	3	,	zv′	=		.
	u				v sin v(v2 sin v − 2)

ЗАДАЧА № 2.2. Продифференцировать сложную функцию u = x3 yz2 , где x =sin t , y = t , z =t 2 .

Решение. Так как u является функцией одной независимой переменной, то речь идет о вычислении обыкновенной производной ut′. Выполняя действия в

соответствии с формулой u′t =u′x xt′ +u′y yt′ +u′z zt′, получим:

ut′ = 3x2 yz

2 cos t + x3 z2

+ 2x3 yz2t .

Вместо x, y и z подставим их в выражения через t:

u′

=3sin 2 t cost t4

t + sin3 t

t 4

+ 4sin3 t t3

t = 0.5t3

t sin 2 t(6t cost + 9sin t).

2 t

ЗАДАЧА № 3. Найти все частные производные и полные дифференциалы

первого и второго порядка от функции z =(2x3 + y2 )2 .

Решение. Находим все частные производные 1-го и 2-го порядков:

z′x =12x2 (2x3 + y2 ),

z′y = 4 y(2x3 + y2 ),

′′

= 24x(2x

+ y

) +12x

=120x

+ 24xy

zxx

′′

+12 y

zxy = 24x

zyy

Находим дифференциалы:

dz = z′xdx + z′y dy =12x2 (2x3 + y2 )dx + 4 y(2x3 + y2 )dy,

′′

=(120x

+24xy

)dx

+48x

ydxdy+(8x

+12y

)dy

z = zxxdx

+2zxydxdy+ zyydy

ЗАДАЧА № 4. Доказать, что функция z =e x

удовлетворяет соотношению:

∂

2 ∂z

2 ∂2 z

− y

∂y2

= 0 .

∂x

Решение. Находим производные:

∂z

∂2 z

=e x

e x ,

e x

−

;

∂x

∂y

∂y2

-7-

далее получаем

∂

∂z

∂

x2e x

−

− ye x

= e x

∂x

Подставляя в левую часть соотношения, получаем:

∂

∂z

2 ∂2 z

2 1

= e x

e x = 0 ,

− y

∂y2

− y

∂x

что и требовалось доказать.

ЗАДАЧА № 5.1. Найти первую и вторую производные неявной функции,

заданной уравнением

ln(2x + 3y) − 2x − y3 =0.

Решение. Производная неявной функции y=y(x), заданной с помощью

уравнения F(x,y)=0, может быть вычислена по формуле

= −

∂F

при

∂F

∂x

∂y

условии, что

≠ 0.

данном

случае

F(x, y) =ln(2x +3y) − 2x − y3 =0.

∂y

Находим ∂F ∂x u ∂F ∂y :

∂F

− 2,

∂F

−3y2 .

∂x

2x + 3y

2x +

∂y

Производная неявной функции равна:

∂y = −

∂F

− 2

2 − 4x − 6 y

∂x

= −

2x + 3y

= −

(3.1)

∂F

3 − 6xy2 −9 y3

∂x

−3y

∂y

2x +3y

Производную второго порядка можно найти последовательным дифференцированием последнего соотношения, рассматривая при этом y как

функцию от x. Получаем:
∂2 y			∂		2 − 4x −6 y
		=		−					=
	2	=		−		2			=
∂x	2				3 −6xy	2	−9 y	3
∂x			∂x		3 −6xy		−9 y

′

−9 y

) −(2 − 4x −6 y)(−6 y

−12xyy

′

− 27 y

′

= −

(−4 − 6 y )(3 − 6xy

y )

(3 −6xy2 −9 y3 )2

Подставляя в это соотношение выражение для

= y′

из формулы (3.1),

получим производную второго порядка для функции y:

y′′xx =12	6x +9y +72x2 y2 +108xy3 +54y4 +6y2 +6xy4 +9y5 +12xy −16x2 y −60xy −54y3 −16x3 y	.

	(3 −6xy2 −9y3 )3

-8-

ЗАДАЧА № 5.2. Найти первые и вторые частные производные неявной функции, заданной уравнением

z2 x − x2 y + y2 z + 2x − y =0.

(3.2)

Решение. Будем дифференцировать по x и по y равенство (3.2), понимая под z неявную функцию двух переменных. Дифференцируем равенство (3.2) по x:

		2xy − z2 − 2		2zz′x x + z2 − 2xy + y2 z′x + 2 = 0.	(3.3)
Найдем z′	=	2xy − z2 − 2		.
Найдем z′	=			.
x		2xz + y2
		2xz + y2
Дифференцируем равенство (3.2) по y:
				2zz′y x − x2 + 2 yz + y2 z′y −1 = 0.	(3.4)
Найдем z′	=	x2 − 2 yz +1	.
Найдем z′	=		.
y		2xz + y2
		2xz + y2

Чтобы найти производные второго порядка, продифференцируем равенство (3.3) сначала по x, потом по y, а равенство (3.4) по y:

′

′′

′

+ y

′′

= 0,

(3.5)

2x(zx )

+ 2xzzxx + 4zzx − 2 y

zxx

′ ′

′′

′

+ y

′′

=0,

(3.6)

2xzx zy

2xzzxy

+ 2zzy

− 2x + 2 yzx

zxy

′

′′

′

′′

′

(3.7)

2x(zy )

2xzzyy

+ 2z + 2 yzy + y

zyy

2 yzy = 0.

Из (3.5), (3.6), (3.7) соответственно найдем:

z′′

2 y − 4zz′x − 2(z′x )2 x

z′′ =

2x − 2 yz′x − 2zz′y − 2xz′x z′y

(3.8)

2zx + y2

2xz + y2

z′′

− 2(z′y )2 x − 2z − 4 yz′y

(3.9)

2xz

+ y2

′

′′ ′′

′′

Подставляя в (3.8), (3.9) выражения для

получим

zy ,

zxx , zyy

, zxy ,

зависящие от x, y, z:

z′′xx =

2 y5 + 6xz4

+12xz2 + 4 y2 z3 +8y2 z −8x3 y2 +16x2 y −8x

(2xz + y2 )3

′′

6x3z2 +6x2 y2z −2xy4 +4xyz3 +6y3z2 +4y3 −2xz2 −2y2z −4x4 y +4y3 −4x2 y +4x

zxy =

(2xz+y2 )3

z′′

= −2

x5 + 2x3 yz + 2x3 + x + 4x2 z3 −3y4 z + 2x2 y3 + 2 y3

(2xz + y2 )3

ЗАДАЧА № 6. Разложить функцию

z = x y

в окрестности точки M (1,1) по

формуле Тейлора, ограничиваясь членами третьего порядка включительно.

Решение. В данном случае формула Тейлора принимает вид

f (x, y)= f (1,1)+

df (1,1)

d 2 f (1,1)

d 3 f (1,1)

+ R ,

(3.10)

-9-

где R3 – дополнительный член формулы Тейлора.

1) Найдем все частные производные функции до 3-го порядка включительно:

′

= yx

y −1

′

= x

ln x ,

′′

y −2

′′

f y

fxx = y(y −1)x

f yy = x

(ln x) ,

′′

y −1

+ yx

y −1

ln x ,

′′′

2)x

y −3

′′′

fxy = x

fxxx = y(y −1)(y −

f yyy = x

(ln x)

′′′

(2 y −1)x

y −2

+ y(y

−1)x

y −2

ln x ,

′′′

= 2x

y −1

ln x + yx

y −1

fxxy

fxyy

(ln x) .

2) Вычислим значения функции и ее частных производных в точке М(1, 1):

′	(1, 1)=1,	′		′′		′′	′′
f (1,1)=1, fx	(1, 1)=1,	f y (1,1)=0 ,		fxx (1,1)= 0 ,		fxy (1,1)=1,	f yy (1,1)=0 ,
′′′	(1,1)= 0 ,	′′′	(1,1)=1,	′′′	(1,1)=0 ,	′′′
fxxx	(1,1)= 0 ,	fxxy	(1,1)=1,	fxyy	(1,1)=0 ,	f yyy (1,1)= 0 .

3) Составим дифференциалы функций, участвующие в формуле (3.10) df (1,1)= fx′(1,1)dx + f y′(1,1)dy = dx ,

f (1,1)

′′

(1,1)dx

′′

= 2dxdy ,

= fxx

+ 2 fxy (1,1)dxdy

f yy (1,1)dy

′′′

dy +

′′′

=3dx

dy .

(1,1)= fxxx (1,1)dx

3 fxxy (1,1)dx

3 fxyy (1,1)dxdy

+ f yyy (1,1)dy

Учитывая, что x0 = y0 =1, dx = x − x0 = x −1, dy = y − y0 = y −1, подставим

найденные значения в (3.10). Получим:

x y =1 + (x −1)+ (x −1)(y −1)+ 1 (x −1)2 (y

−1)+ R .

ЗАДАЧА № 7.1. Составить уравнения касательной плоскости и нормали к

поверхности z = excos y

в точке

M 1,π,

1 .

Решение. Если уравнение поверхности задано в явной форме z = f (x, y), то

уравнение касательной плоскости в точке M (x0 , y0 , z0 ) имеет вид

z − z0 = fx′(x0 , y0 )(x − x0 )+ f y′(x0 , y0 )(y − y0 ),

а уравнение нормали

x − x0

y − y0

z − z0

fx′(x0 , y0 )

f y′(x0 , y0 )

−1

Найдем частные производные

fx′,

f y′:

f y′ =ex cos y (− xsin y).

fx′ = ex cos y cos y ,

Найдем значения

частных

производных

точке

N(1,π):

fx′(1,π)= −1 ,

f y′(1,π)= 0 .

Подставляя

найденные

значения

координаты

точки

М в

уравнения касательной

плоскости

нормали,

соответственно

получим:

z −

= −

x −1

или

x + ez − 2 =0

–

уравнение

касательной

плоскости,

x −1

y −π

z −1 e

x −1

y −π

z −1 e

или

– уравнение нормали.

−1 e

−1

-10-

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.04.2015944.25 Кб17AI_lek.pdf
#
20.04.2015717.79 Кб767American_Crime_Stories_Oxford_Bookworms-6.pdf
#
20.04.2015792.74 Кб21Androsova_002.pdf
#
16.11.2018433.15 Кб10Anin_kursach.doc
#
20.04.2015447.87 Кб10Anisimov.pdf
#
20.04.2015486.51 Кб25Ankilov_Goryacheva_Rasputko.pdf
#
20.04.2015207.36 Кб7AONI.doc
#
23.03.2016302.59 Кб7audit 3.doc Курсовая работа.doc
#
25.11.2019163.33 Кб1Audit.doc
#
17.04.20191.07 Mб18bilety_sidorov.docx
#
22.04.2019210.96 Кб5BILYeT_1.docx