Системы счисления и простейшие числовые коды

Каждый человек в повседневной деятельности сталкивается с вычислениями (счетом). Однако, получив, например, в результате вычисления число 1234,56, многие и не подозревают, что пользовались десятичной системой счисления, а само это число есть сокращенная запись полинома 1 ^. 10³ + 2 ^. 10² + 3 ^. 10¹ + 4 ^. 10⁰ + 5 ^. 10^-1 + 6 ^. 10^-2.

Число - это действительная величина в определенной системе счисления, выражающая количество однородных объектов. Системой счисления называется совокупность правил записи любых чисел ограниченным количеством символов, называемых цифрами, позволяющая установить взаимнооднозначное соответствие между любым числом и его представлением и наименованием. Цифра - это символ, изображающий конкретное число. Разрядом числа называется позиция цифры в изображении числа. Основанием или базой (p) системы счисления называется количество различных цифр, применяемых для написания числа: 0, 1,..., p – 1.

Система счисления называется позиционной, если количество, определяемое каждой цифрой, входящей в запись числа, зависит от ее положения (позиции) в ряду цифр, изображающих это число. Число, на которое умножается цифра данного разряда, чтобы получить это количество, называется весом разряда. Среди позиционных систем особое значение имеют системы счисления, в которых веса отдельных разрядов представляют собой геометрическую прогрессию со знаменателем, равным основанию системы счисления p. В этом случае говорят о системах счисления с естественным порядком весов. Например, разряды десятичного числа 1234,56 имеют веса 10³ = 1000; 10² = 100; 10¹ = 10; 10⁰ = 1; 10^-1 = 0,1; 10^-2 = 0,01. Существуют системы счисления с искуственным порядком весов. Позиционные системы счисления с общим основанием для всех разрядов называются однородными. Они характеризуются тем, что цифры во всех разрядах используются из одного и того же множества 0, 1,..., p – 1. Наибольшее распространение получили позиционные однородные системы счисления, для которых можно сформулировать три важные характеристики:

• количество используемых цифр равно основанию системы счисления;

• наибольшая цифра на единицу меньше основания;

• каждая цифра в числе умножается на основание в степени, значение которой определяется позицией цифры в числе.

Широко распространенная десятичная система счисления p = 10 (по-видимому ее основой явились 10 пальцев на руках человека) изобретена в Индии около 400 -х г. н. э. В 800-х г. н. э. она получила широкое распространение в арабских странах, откуда приблизительно в начале XIII века попала в Европу, поэтому цифры десятичной системы счисления 0, 1, ... , 9 традиционно (но ошибочно) называют арабскими.

Если позиционная система для каждой цифры имеет отдельный символ, то она называется системой с непосредственным представлением чисел. Таковой является, например, десятичная система счисления. Позиционная система называется системой с кодированным представлением чисел, когда количество символов меньше, чем количество цифр, а каждая цифра кодируется определенной комбинацией из нескольких символов. Таковой является, например, двоично-десятичная система счисления (0 = 0000, 1 = 0001, ... , 9 = 1001), в которой десять цифр, но только два символа.

До изобретения позиционных систем счисления использовались непозиционные системы счисления, в которых значение цифры не зависит от ее положения в ряду цифр, изображающих число. Среди них наиболее известны римская система счисления, унитарная, а также современная система счисления в остаточных классах.

В римской системе счисления используют следующие цифры: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. В этой системе число 1997 будет записано как MCMXCVII. Римские цифры в настоящее время в основном используются для обозначения юбилейных дат, нумерации в книгах страниц введения, глав, строф в стихотворениях, на циферблатах часов и т. п.

В унитарной системе число представляется общей совокупностью однородных объектов (палочек, черточек, импульсов и т. п.) Такая система используется в электромеханических городских часах, в аналого-цифровых преобразователях и др.

В системе остаточных классов числа представляются своими остатками от деления на выбранную систему взаимно простых оснований [1] .

Достоинства и недостатки различных систем счисления, используемых при технической реализации цифровых устройств, могут быть выявлены, исходя из следующих практически важных требований:

• возможность представления любого числа в заданном диапазоне;

• единственность представления, когда любой числовой код соответствует только одному числу;

• простота выполнения арифметических и логических операций над числами.

Главным преимуществом позиционных систем счисления по сравнению с непозиционными является удобство представления чисел и простота выполнения арифметических и логических операций.

Недостатком позиционных систем счисления является наличие межразрядных связей (переносов и заемов) при выполнении арифметических операций над числами, то есть невозможность выполнения арифметических операций как поразрядных (когда результат операции не зависит от ее результата в остальных разрядах).

Недостатками непозиционных систем счисления являются неудобство выполнения арифметических и логических операций и трудности при записи и восприятии больших чисел.

В системе остаточных классов все операции могут выполняться параллельно над цифрами каждого разряда в отдельности. Однако ей присущ и ряд недостатков: ограниченность действия этой системы полем целых положительных чисел, трудность определения соотношения чисел по величине, определения выхода результата операции из диапазона, отсутствие наглядной связи между числом и его представлением, не позволяющем оценить величину числа без перевода его в позиционную систему счисления, трудность выполнения операций деления и округления и др.

Несмотря на то, что в практике ручных вычислительных работ наибольшее распространение получила десятичная позиционная однородная система счисления, она не является удобной для использования в цифровых устройствах, в частности в электронных вычислительных машинах (ЭВМ). Это связано прежде всего с трудностью технической реализации десяти различных уровней сигналов при одновременном обеспечении высокой помехоустойчивости.

Минимальное количество цифр, которое может быть принято в позиционной системе счисления, равно двум (0 и 1). Именно двоичная система счисления и нашла самое широкое применение в цифровых устройствах и ЭВМ в силу следующих очевидных преимуществ:

• простота технической реализации двух сигналов, кодирующих числа 0 и 1, которые в большинстве случаев отличаются друг от друга не столько количественно, сколько качественно;

• обеспечиваются высокие помехоустойчивость, надежность и быстродействие;

• легко выполняются арифметические и логические операции, что значительно упрощает схемотехнику арифметических и логических узлов, а их анализ и синтез просто выполняется на основе аппарата булевой алгебры и теории конечных автоматов;

• экономичность.

Эти преимущества полностью перекрывают такие недостатки двоичной (а также двоично-кодированной) системы счисления, как:

• длинная запись числа;

• необходимость преобразования входных и выходных данных из привычной человеку десятичной системы счисления в двоичную;

• трудность чтения и восприятия чисел.

Сокращение длины записи двоичных чисел легко обеспечивается применением систем счисления с кратным основанием. Если для оснований систем счисления p₁ и p₂ справедливо соотношение p₂ = p₁^k, где k – цeлое положительное число, то такие системы называются системами счисления с кратными основаниями. Примером таких систем являются двоичная, восьмеричная и шестнадцатеричная системы (2³ = 8; 2⁴=16). Хорошее знание этих систем счисления является обязательным для каждого, кто решил серьезно заняться изучением цифровой техники. Восьмеричная и шестнадцатеричная системы счисления в основном используются как вспомогательные для сокращения трудоемкости ручной обработки кодов чисел, команд и т. п. при подготовке программ, чтобы избежать чтения и записи громоздких двоичных чисел.

Хотя перевод чисел из десятичной системы счисления в двоичную и обратно в ЭВМ осуществляется автоматически (аппаратно или программно), надо знать и ручные методы таких переводов. Наиболее распространены два метода перевода чисел из одной системы счисления в другую: табличный и расчетный.

При первом методе используются специальные таблицы соответствия чисел в различных системах счисления. Этот метод громоздкий, но применим как к позиционным, так и к непозиционным системам. Такие таблицы очень удобны на начальном этапе ознакомления с новой системой. Например, полезно запомнить четырехразрядные двоичные эквиваленты десятичных цифр (см. табл.1).

Расчетный метод универсальнее и удобнее, но применим он только к позиционным системам счисления. В практике встречаются три случая перевода: целых чисел, правильных дробей и неправильных дробей. Правильной дробью называется дробь, у которой числитель меньше знаменателя, то есть число, меньшее единицы (например: 0,6; 3/7; 0,33...). Неправильной дробью называется дробь, у которой числитель равен или больше знаменателя, то есть число большее или равное единицы (например: 3/3; 7/3; 1,23; 15,36).

Таблица 1.
Десятичное число	Двоичное число	Восьмеричное число	Шестнадцатиричное число
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Алгоритмы перевода чисел в другую систему счисления, использующие арифметику исходной системы счисления (p).

Правило перевода целых чисел. Будем обозначать целое число X по основанию p как X_(p). Если основание p не указывается, то, по умолчанию, считают, что число представлено в десятичной системе счисления.

Для перевода целого числа X_(p) в систему счисления с основанием q необходимо по правилам арифметики исходной p-системы делить данное число X_(p) на новое основание q_(p) до получения целого остатка, меньшего q. Полученное частное необходимо снова делить на основание q до получения целого остатка, меньшего q, и т. д. до тех пор, пока последнее частное будет меньше нового основания q. Число X_(q) в системе счисления с основанием q представляется последовательностью остатков деления в порядке, обратном их получения, причем старшую цифру в числе X_(q) дает последний остаток (метод последовательного деления). Поскольку используется арифметика исходной системы, то таким способом удобно переводить из десятичной системы счисления в другие системы.

Пример. Перевести число 181 в систему счисления с основанием 2.

_181	2
180	_90	2
1	90	_45	2
	0	44	_22	2
		1	22	_11	2
			0	10	_5	2
				1	4	_2	2
					1	2	1	Старший разряд числа
						0		в двоичной системе

Ответ: 181 = 10110101₍₂₎.

Правило перевода правильной дроби. X_(p)X_(q). Перевод правильной дроби X_(p) в систему счисления с основанием q заключается в последовательном умножении этой дроби на новое основание q_(p) (по правилам исходной p-системы), причем перемножению подвергаются только дробные части. Дробь X_(q) в системе счисления с новым основанием представляется в виде последовательности целых частей произведений в порядке их получения, причем старший разряд является целой частью первого произведения. Если требуемая точность перевода есть q^-k , то число указанных последовательных произведений равно k (метод последовательного умножения).

Пример. Перевести десятичную дробь 0,789 в двоичную с точностью 2^-6. Заданное число умножаем последовательно 6 раз на 2:

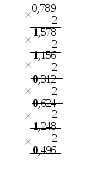
Ответ: 0,789 = 0,110010₍₂₎.

Правило перевода неправильной дроби. Для чисел, имеющих как целую, так и дробную части, перевод из одной системы счисления в другую осуществляется отдельно для целой и дробной части по правилам, указанным выше.

Алгоритмы перевода чисел в другую систему счисления, использующие арифметику новой системы счисления (q).

Для перевода чисел в десятичную систему из любой другой удобно пользоваться арифметикой десятичной системы. В этих случаях используются алгоритмы перевода целых и дробных чисел, представленных в виде полинома, причем веса разрядов и все цифры надо представлять в новой системе счисления и все арифметические операции выполнять по правилам новой системы счисления.

Пример. 10110101₍₂₎ = 1^.2⁷ + 0^.2⁶ + 1^.2⁵ + 1^.2⁴ + 0^.2³ + 1^.2² + 0^.2¹ + 1^.2⁰ = 181. 0,110010₍₂₎ = 1^.2^-1 + 1^. 2^-2 + 0^.2^-3 + 0^.2^-4 + 1^.2^-5 + 0^.2^-6 = 0,78125.

Перевод чисел в системах счисления с кратными основаниями.

Перевод чисел в системах с кратными основаниями не требует выполнения арифметических действий и выполняется с использованием табличной шифрации (см. табл. 1).

Первый случай. X_(p)X_(q); p = q^k. Каждая цифра числа X_(p) заменяется своим k-разрядным представлением в q-системе.

Пример. p = 8; q = 2; k = 3. Исходное число: 123,4566₍₈₎.

1	2	3,	4	5	6	6
001	010	011,	100	101	110	110

Каждая восьмеричная цифра заменена двоичной триадой (см. выделенную штриховой линией часть табл. 1).

Примечание: незначащие нули в старших и младших разрядах двоичного числа можно опустить. Ответ: 1010011,10010111011₍₂₎.

Пример. p = 16; q = 2; k = 4. Исходное число: 79A,2C₍₁₆₎.

7	9	А,	2	С
0111	1001	1010,	0010	1100

Каждая шестнадцатеричная цифра заменена двоичной тетрадой.

Ответ: 11110011010,001011₍₂₎. Здесь также опущены незначащие нули в младших и старших разрядах при записи двоичного числа.

Второй случай. X_(p) X_(q); q = p^k. Число в исходной p-системе разбивается на группы по k разрядов вправо и влево от запятой, причем в неполные группы добавляются нули (справа - для дробной части, слева - для целой). Каждая группа из k цифр p-системы заменяется одним эквивалентным ей символом q-системы.

Пример. Перевести двоичное число 1010011,10010111011 в восьмеричную систему.

001	010	011,	100	101	110	110
1	2	3,	4	5	6	6

Ответ: 123,4566₍₈₎.

Пример. Перевести двоичное число 11110011010,001011 в шестнадцатеричную систему.

0111	1001	1010,	0010	1100
7	9	A ,	2	C

Ответ: 79A,2C₍₁₆₎.

Приведенные примеры показывают, что представление двоичного числа в восьмеричной (шестнадцатеричной) системе счисления сокращает длину записи в три (четыре) раза.

Рассмотрение дальнейшего материала будет вестись для двоичных чисел, так как в большинстве случаев в цифровых устройствах используется двоичная система счисления.

Разрядность операционных устройств, регистров и ячеек памяти фиксирована, что ограничивает как диапазон представления, так и точность чисел. Количество разрядов ограничено длиной разрядной сетки, под которой понимается фиксированная совокупность двоичных разрядов, предназначенных для приема, обработки, хранения и выдачи данных в виде двоичных кодов. Данные - это обобщающее понятие для содержимого разрядной сетки, в качестве которого могут быть:

1. числа без знака;

2. числа со знаком, представленные в различных формах и форматах;

3. алфавитно-цифровые (текстовые) коды символов;

4. системная информация о состоянии аппаратных и программных средств, представленная в регистре состояния (перенос, переполнение, знак числа, нулевое состояние, режим работы и т.д.);

5. команды;

6. адреса;

7. константы;

8. маски;

9. смещение и т.п.

В каждом такте машинного времени все разряды сетки обрабатываются одновременно. Доступность для пользователя данных, обрабатываемых в разрядной сетке, определяет два вида кодов: параллельный, когда в каждый момент времени все разряды сетки доступны, и последовательный, когда в каждый момент времени доступен только либо младший, либо старший разряды сетки. Говорят, что данные, представленные параллельным кодом, доступны за один такт, а данные, представленные последовательным кодом, доступны за n тактов, где n - разрядность сетки. Если разрядность данных превышает длину сетки, то их обработка ведется по частям.

Рассматривая данные как целые числа без знака, (так называемый натуральный код) (см. рис. 1, а) , можно ввести следующие важные параметры разрядной сетки:

• емкость сетки М - это максимальное количество различных чисел, представимых в ней (для двоичных чисел М = 2ⁿ);

• максимальное число N_max, представимое в ней (для двоичных чисел N_max = 2ⁿ –1);

• минимальное число N_min = 1;

• динамический диапазон разрядной сетки d = (N_max)/(N_min) = 2ⁿ – 1.

Очевидно, что относительная точность представления целого числа зависит от его абсолютной величины и может меняться в широких пределах.

Р

а) Число без знака б) Прямой код

128 64 32 16 8 4 2 1 нет 64 32 16 8 4 2 1

	b7	b6	b5	b4	b3	b2	b1	b0		+122	0	1	1	1	1	0	1	0
122	0	1	1	1	1	0	1	0		–122	1	1	1	1	1	0	1	0

в) Обратный код г) Дополнительный код

–127 64 32 16 8 4 2 1 –128 64 32 16 8 4 2 1

+122	0	1	1	1	1	0	1	0		+122	0	1	1	1	1	0	1	0
–122	1	0	0	0	0	1	0	1		–122	1	0	0	0	0	1	1	0

д) Смещенный код с “+0” е) Смещенный код с “–0”

64 32 16 8 4 2 1 64 32 16 8 4 2 1

+122	1	1	1	1	1	0	1	0		+122	1	1	1	1	1	0	0	1
–122	0	0	0	0	0	1	1	0		–122	0	0	0	0	0	1	0	1

ис. 1. Числовые коды в восьмиразрядной сетке,

где =–(1– b₇)128; =–(1– b₇)128+1.

Эти же числовые параметры справедливы и для представления чисел со знаком в естественной форме (с фиксированной запятой (точкой)). Эта форма представления чисел предполагает, что положение запятой, отделяющей целую часть числа от дробной, фиксировано в разрядной сетке (запятая подразумевается, но аппаратно не реализуется).

Для представления знака выделяется специальный знаковый разряд сетки, причем обычно это левый (старший) ее разряд. Используются два основных способа расположения фиксированной запятой: перед старшим разрядом - для правильных дробей или после младшего разряда - для целых чисел.

Возможность построения сравнительно несложных операционных устройств с высоким быстродействием - одно из важных свойств представления чисел в форме с фиксированной запятой. Представление чисел в этой форме используется как основное и единственное лишь в специализированных ЭВМ и сравнительно небольших по своим вычислительным возможностям машинах, применяемых в системах передачи данных, для управления технологическими процессами и обработки измерительной информации в реальном масштабе времени.

Наибольшее распространение получило представление целых чисел со знаком как целых, что и используется в дальнейшем изложении материала. Выбор числовых кодов для представления целых чисел со знаком осуществляется с учетом следующих факторов: общее количество положительных и отрицательных чисел не может превышать емкость разрядной сетки; целесообразно, чтобы количество положительных и отрицательных чисел было бы одинаковым; для выполнения основных арифметических и логических операций над числовыми кодами желательно использовать одну и ту же аппаратуру.

Число со знаком изображается знаком числа (“+” - для положительных чисел, “–” - для отрицательных) и модулем числа. Полезно помнить также, что знаки “+” и “–” используются и для обозначения арифметических операций “сложение” и “вычитание” соответственно.

Поскольку аппаратура ЭВМ выполняется на элементах булевой алгебры и для представления двоичных состояний применяют символы 0 и 1, то эти же символы следует использовать и для обозначения знака числа.

Конкретную иллюстрацию примеров различных числовых кодов будем вести для разрядной сетки с n = 8. Сетку с такой длиной называют байтом. Байт является основной единицей для двоичного кодирования текстовой (литерной) информации не только в ЭВМ, но и в системах передачи данных, а также является наименьшей адресуемой единицей данных в большинстве ЭВМ. Отдельные разряды сетки обозначим индексированной буквой b_i, i = 0,..., n-1 (bit - binary digit), причем 2ⁱ будет являться весом двоичного разряда. Полезно помнить, что число без знака (см. рис. 1, а) имеет положительные веса 2ⁱ во всех разрядах сетки. Для сетки с n = 8 имеем: М = 256₍₁₀₎ = 100000000₍₂₎; N_max = 255₍₁₀₎ = 11111111₍₂₎. B дальнейшем индексы 10 и 2 опустим из-за очевидности записи чисел. Обратите также внимание, что для записи ‘М’ в виде двоичного числа требуется девять разрядов, то есть такое число нельзя представить в 8-ми разрядной сетке (емкость разрядной сетки равна весу разряда, следующего за ее старшим разрядом).

Кодируя разряд b₇ символом 0 для знака “+” и символом 1 для знака ”–”, а в разрядах b₆,...,b₀ помещая модуль числа, получим представление чисел со знаком в прямом коде (см. рис. 1, б). Важной особенностью прямого кода является то, что цифру знакового разряда и цифровую часть числа нельзя рассматривать как единое целое, так как кодируется только знак числа. Максимальное положительное число равно +127 = 01111111, то есть (2^n–1 –1). Минимальное (максимальное по модулю) отрицательное число равно –127 = 11111111. Нуль имеет два представления: положительный нуль +0= 00000000 и отрицательный нуль –0 = 10000000.

Достоинства прямого кода: цифровые разряды содержат модуль представляемых чисел, что обеспечивает наглядность их считывания в этом коде; просто осуществляется сложение чисел, имеющих одинаковые знаки, а также деление и умножение, когда операции со знаками и модулями ведутся раздельно; количество положительных и отрицательных чисел одинаково.

Недостатки прямого кода: сложно складывать и вычитать числа с разными знаками, так как, например при сложении, приходится определять большее по модулю число, производить вычитание чисел и присваивать результату знак большего по модулю числа; нуль имеет два представления.

Прямой код широко используется для хранения чисел в памяти, в устройствах ввода-вывода, в цифроаналоговых и аналогоцифровых преобразователях (ЦАП и АЦП).

В общем случае представление прямого двоичного кода в n-разрядной сетке определяется как

где А - величина, равная весу старшего разряда сетки (А = 2^n–1 для целых чисел и А =1 для правильных дробей), а |Х| ≤ А–1 = 2^n–1 –1.

Рассмотрим теперь следующий пример. Пусть требуется вычислить разность двух чисел 126 = 1111110 (уменьшаемое) и 122 = 1111010 (вычитаемое). Здесь двоичные числа представлены пока как семиразрядные, так как разряд b₇ кодирует знак числа. Очевидно, что модуль положительного и отрицательного числа не может быть больше 2^n–1 –1, что при n = 8 дает 127, а как кодируется знак будет ясно чуть ниже.

Разность указанных чисел можно представить как

126 – 122 = 126 + (255 - 122) - 255,

где 255 = 11111111 = N_max для n = 8.

Выражение в скобках (255 - 122) называется дополнением отрицательного числа –122 до N_max, а численное значение разности 133 = 10000101 обратным кодом отрицательного двоичного числа –122₍₁₀₎ (см. рис. 1, в). Наличие 1 в знаковом разряде обратного кода отрицательного числа говорит о том, что знак “–” кодируется единицей, а “+” нулем. Итак, обратный код отрицательного двоичного числа представляет собой дополнение исходного числа до наибольшего числа без знака, размещаемого в разрядной сетке, а получение обратного кода отрицательного числа сводится к поразрядному инвертированию n-разрядного двоичного кода модуля этого числа (в том числе и знакового разряда). Отсюда, в частности, ясно происхождение термина “обратный”, то есть инверсный. Проведем теперь вычисление 126 + 133 - 255, представив числа в двоичных кодах:

Так как выделенная единица результата первого суммирования выпадает из 8-ми разрядной сетки, то она уменьшает полученный результат на 256, (вес девятого разряда), а нам надо было уменьшить результат на 255, следовательно для получения правильного результата нужно к первой сумме добавить единицу (это делается с помощью так называемого циклического переноса аппаратными средствами, когда перенос в несуществующий девятый разряд прибавляется в младший разряд сумматора чисел). Наличие нуля в знаковом разряде суммы говорит о том, что результат положительный, а сама разность равна 4.

Рассмотренный пример показывает, что вычитание числа (или сложение с отрицательным числом) можно заменить сложением с обратным кодом отрицательного числа с прибавлением в младший разряд результата единицы.

Достоинства обратного кода: простота его получения; легко осуществляется сложение чисел с разными знаками; количество отрицательных и положительных чисел одинаково; так как для отрицательных чисел здесь кодируются и знак числа, и его модуль, то при выполнении арифметических операций сложения и вычитания цифру знакового разряда и цифровую часть числа можно рассматривать как единое целое и обращаться со знаковым разрядом так же, как и с разрядами цифровой части числа. Причем веса цифровых разрядов положительные и равны 2ⁱ, а вес знакового разряда отрицательный и равен 2^n–1 –1 (см. рис.1, в).

Недостатки обратного кода: нуль имеет два представления: положительный +0 = 00000000 и отрицательный –0 = 11111111; требуется аппаратная реализация циклического переноса.

В общем случае представление обратного двоичного кода в n-разрядной сетке определяется как:

где В - наибольшее число без знака, размещающееся вn-разрядной сетке (В = 2^n–1 –1 для целых чисел и В = 2 – 2^–(n–1) для правильных дробей), а |Х| ≤ 2^n–1 –1.