Дискретная математика / Дискретка

Стохастический эксперимент  это эксперимент, результат которого заранее (до его проведения) предугадать нельзя.

Каждый неразложимый исход опыта (эксперимента) называется элементарным событием и обозначается . Множество всех элементарных событий, относящихся к одному и тому же эксперименту, называется пространством элементарных событий и обозначается .

Случайным событием или просто событием называется любое подмножество пространства элементарных событий . События обозначают прописными буквами латинского алфавита A, B, C, . . .

Свойства элементарных событий:

• элементарные события являются взаимно исключающими друг друга;

• в результате опыта обязательно происходит одно из элементарных событий;

• каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А.

Пусть  пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события А выделим совокупность всех элементарных событий, наступление которых необходимо влечет наступление А. Говорят, что эти элементарные события благоприятствуют событию А. (Множество этих элементарных событий обозначают тем же символом А, что и соответствующее событие).

Таким образом, событие А состоит в том, что произошло одно из элементарных событий, входящих в указанное множество А. То есть мы отождествляем событие А и соответствующее ему множество А элементарных событий.

Событие, состоящее из всех возможных элементарных событий , называется достоверным и обозначается (так же, как и пространство элементарных событий). (Достоверное событие наступает в результате появления любого элементарного события. Но тогда ему благоприятствует любое ).

Невозможным называется событие, не наступающее ни при каком элементарном событии. Ему соответствует пустое множество элементарных событий: .

Соотношения между событиями:

1. Если каждое появление события А сопровождается появлением события В, то говорят, что А влечет В, или А является частным случаем В, или В является следствием события А, или А благоприятствует В ( ). Если , то каждое элементарное событие, входящее в А, содержится в событии В.

2. События А и В называются равносильными (равными, эквивалентными) ( ), если они состоят из одних и тех же элементарных событий, т.е. всегда происходят или не происходят одновременно.

3. Суммой (объединением) событий А и В ( или ) называется событие, которое состоит из элементарных событий, входящих хотя бы в одно из событий А и В, т. е. событие, происходящее тогда и только тогда, когда происходит хотя бы одно из событий А и В (или А или В)

Очевидно, что: ; , А + А = А.

4. Произведением (пересечением) двух событий А и В (АВ или ) называется событие, которое состоит из элементарных событий, входящих и в событие А, и в событие В одновременно, т. е. событие, происходящее только тогда, когда происходит и событие А, и событие В.

Очевидно, что: ; ; .

5. Два события называются несовместными, если их одновременное появление в опыте невозможно. Следовательно, если А и В несовместны, то АВ = .

Элементарные события попарно несовместны: при .

6. Событием, противоположным событию А () называется событие, которое состоит из всех элементарных событий, не входящих в А. Противоположное событие происходит тогда и только тогда, когда А не происходит.

Очевидно, что: ; .

7. Разностью событий А и В ( или ) называется событие, происходящее тогда и только тогда, когда происходит событие А и не происходит событие В.

Очевидно, что: ; .

8. События образуют полную группу событий, если .

Свойства операций над событиями:

_1. ; 2. ;

3. ; 4. A + B = B + A, AB = BA ;

5. A(BC) = (AB)C, 6. A + (B + C) = (A + B) + C ;

6. A(B + C) = AB + AC ; 7. .

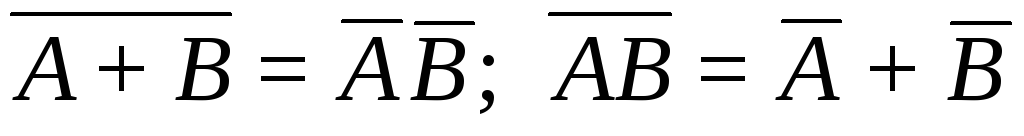Рассмотрим пространство элементарных событий , соответствующее некоторому стохастическому эксперименту, и пусть F  некоторая система случайных событий.

Система событий F называется алгеброй событий, если выполняются условия:

1) ;

2) если ;

3) если А и В и .

Отсюда следует, что применяя любые из введенных выше операций к произвольной системе событий из F, получим событие, так же принадлежащее F. Таким образом, алгеброй событий называется класс событий, замкнутый относительно операций объединения, пересечения и дополнения.

Вероятность события численно характеризует степень объективной возможности этого события.

Пусть  пространство элементарных событий некоторого стохастического эксперимента и в выделена система событий F, являющаяся алгеброй событий.

Определение: Если каждому событию поставлено в соответствие число р(А) и верны свойства:

1) ; 2) ;

3) если А и В несовместны , то р(А+В) = р(А) + р(В),

тогда число р(А) называется вероятностью случайного события А.

Свойства вероятности:

1. ;

2. Если события A и В  несовместны, то р(А+В) = р(А) + р(В);

3. .

Пространство элементарных событий с выделенной в нем алгеброй событий F и определенной на измеримом пространстве (, F) вероятностной мерой р(А), , называется вероятностным пространством и обозначается (, F, p(A)).

Классическое определение вероятности

Если множество элементарных событий состоит из n равновозможных элементарных событий, то вероятность р(А) события А равна числу m элементарных событий, входящих в А, деленному на число всех элементарных событий, т. е. .

Условной вероятностью называют вероятность события А, вычисленную в предположении, что событие В уже наступило.

Условная вероятность события А при условии, что событие В произошло, определяется формулой

, где .

События А и В – называются независимыми, если при происхождении одного из них не изменяется вероятность происхождения другого. Для независимых событий выполняется равенство .

Очевидно, что для независимых событий справедливо:

.

Смысл определения независимости событий заключается в том, что если произошло одно из независимых событий, то это никак не влияет на вероятность появления другого события.

События называются независимыми в совокупности, если для любых k из них выполняется соотношение:

.

Если это соотношение выполняется при k = 2, то события называются попарно независимыми.

Теорема сложения. Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:

p(А+В) = p(А) + p(В) – p(АВ).

Если события А и В несовместны, то p(А+В) = p(А) + p(В).

Теорема умножения. Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило: