
алгебра и геометрия 2010
.docxАлгебра и геометрия
Вариант 11
-
а) Доказать, что множество квадратных
 матриц с действительными элементами
и нулевыми угловыми элементами с
обычными операциями сложения и умножения
на числа образует векторное пространство
над
матриц с действительными элементами
и нулевыми угловыми элементами с
обычными операциями сложения и умножения
на числа образует векторное пространство
над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, с нулевой суммой
первой и последней координаты. а)
Доказать, что
,
состоящее из строк, с нулевой суммой
первой и последней координаты. а)
Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
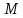 .
. -
Векторы
 и x
заданы своими координатами в некотором
базисе пространства
и x
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
е1 = (1,3,0,5) v1 = (1,0,0,1)
e2 = (0,2,0,2) v2 = (0,1,0,0)
e3 = (1,2,2,3) v3 = (0,0,1,0)
e4 = (0,0,0,1) v4 = (0,0,0,1)
x=(-i, i, i+1,0)
Алгебра и геометрия
Вариант 12
-
а) Доказать, что все многочлены из
 ,
так что
,
так что
 образуют относительно обычного сложения
и умножения на числа из
образуют относительно обычного сложения
и умножения на числа из
 векторное пространство над
векторное пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
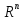 ,
состоящее из строк, с одинаковыми
нечетными координатами и одинаковыми
четными координатами. а) Доказать, что
,
состоящее из строк, с одинаковыми
нечетными координатами и одинаковыми
четными координатами. а) Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
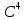 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (1,3,0,5) v1 = (1,0,0,1)
e2 = (0,2,0,2) v2 = (0,1,0,0)
e3 = (1,2,2,3) v3 = (0,0,1,1)
e4 = (0,0,0,1) v4 = (0,0,0,1)
x=(-i, 2+i, i, 1)
Алгебра и геометрия
Вариант 13
-
а) Доказать, что множество квадратных
 матриц с действительными элементами
и нулевой суммой крайних элементов (то
есть элементов, стоящих в первой и
последней строке и первом и последнем
столбце) является векторным пространством
над
матриц с действительными элементами
и нулевой суммой крайних элементов (то
есть элементов, стоящих в первой и
последней строке и первом и последнем
столбце) является векторным пространством
над
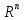 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, с нулевой суммой
всех координат. а) Доказать, что
,
состоящее из строк, с нулевой суммой
всех координат. а) Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
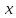 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
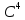 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (1,0,2,1) v1 = (1,3,0,5)
e2 = (0,2,0,2) v2 = (0,1,0,2)
e3 = (3,1,4,5) v3 = (1,2,1,3)
e4 = (1,0,0,0) v4 = (0,0,0,1)
x=(i+1, i-1, 1, i)
Алгебра и геометрия
Вариант 14
-
а) Доказать, что множество квадратных
 матриц с действительными элементами
и нулевой суммой крайних элементов (то
есть элементов, стоящих в первой и
последней строке и первом и последнем
столбце) является векторным пространством
над
матриц с действительными элементами
и нулевой суммой крайних элементов (то
есть элементов, стоящих в первой и
последней строке и первом и последнем
столбце) является векторным пространством
над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, с нулевой суммой
всех координат. а) Доказать, что
,
состоящее из строк, с нулевой суммой
всех координат. а) Доказать, что
 – подпространство в
– подпространство в
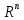 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (2,3,0,5) v1 = (1,0,0,1)
e2 = (0,2,0,2) v2 = (0,1,0,1)
e3 = (1,2,1,3) v3 = (0,0,1,1)
e4 = (0,0,0,1) v4 = (0,0,0,1)
x=(i, 2+ i, 2i, 0)
Алгебра и геометрия
Вариант 15
-
а) Доказать, что множество всех нижнетреугольных
 матриц с действительными элементами
и обычными операциями сложения и
умножения на числа образует векторное
пространство над
матриц с действительными элементами
и обычными операциями сложения и
умножения на числа образует векторное
пространство над
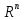 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
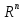 ,
состоящее из строк, у которых последняя
координата равна нулю. а) Доказать, что
,
состоящее из строк, у которых последняя
координата равна нулю. а) Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
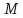 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
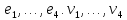 и
и
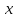 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
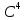 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
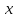 в обоих базисах.
в обоих базисах.
e1 = (1,1,1,1) v1 = (0,1,1,1)
e2 = (1,1,-1,-1) v2 = (1,0,1,1)
e3 = (1,-1,1,-1) v3 = (1,1,0,1)
e4 = (1,-1,-1,1) v4 = (1,1,1,0)
x=(i, - i, 1, 2i)
Алгебра и геометрия
Вариант 16
-
а) Доказать, что множество всех квадратных
 матриц с действительными элементами,
имеющих одинаковые числа на главной
диагонали с обычными операциями сложения
и умножения на числа образует векторное
пространство над
матриц с действительными элементами,
имеющих одинаковые числа на главной
диагонали с обычными операциями сложения
и умножения на числа образует векторное
пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, сумма координат
которых, равна нулю. а) Доказать, что
,
состоящее из строк, сумма координат
которых, равна нулю. а) Доказать, что
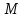 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
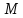 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (3,3,-4,-3) v1 = (1,0,0,0)
e2 = (0,6,1,-1) v2 = (0,1,0,0)
e3 = (5,4,2,1) v3 = (0,0,1,0)
e4 = (2,3,3,1) v4 = (0,0,0,1)
x=(i, - i, 1, 2i)
Алгебра и геометрия
Вариант 17
-
а) Доказать, что множество всех квадратных
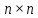 матриц с действительными элементами,
и нулевой суммой элементов, стоящих на
главной диагонали с обычными операциями
сложения и умножения на числа образует
векторное пространство над
матриц с действительными элементами,
и нулевой суммой элементов, стоящих на
главной диагонали с обычными операциями
сложения и умножения на числа образует
векторное пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
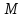 – подмножество в
– подмножество в
 ,
состоящее из строк, сумма нечетных
координат которых, равна нулю. а)
Доказать, что
,
состоящее из строк, сумма нечетных
координат которых, равна нулю. а)
Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
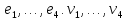 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (1,3,0,5) v1 = (1,1,1,1)
e2 = (0,1,0,2) v2 = (0,1,1,1)
e3 = (1,2,1,3) v3 = (0,0,1,1)
e4 = (0,0,0,1) v4 = (0,0,0,1)
x=(i, -2i, 3+i, 1)
Алгебра и геометрия
Вариант 18
-
а) Доказать, что все многочлены с действительными коэффициентами степени
 ,
имеющие корень 0 относительно обычного
сложения и умножения на числа, образуют
векторное пространство над
,
имеющие корень 0 относительно обычного
сложения и умножения на числа, образуют
векторное пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, сумма первой и
последней координат которых равна 0.
а) Доказать, что
,
состоящее из строк, сумма первой и
последней координат которых равна 0.
а) Доказать, что
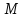 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
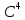 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
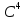 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (0,1,1,1) v1 = (1,0,0,0)
e2 = (1,0,1,1) v2 = (0,1,1,1)
e3 = (1,1,0,1) v3 = (0,0,1,0)
e4 = (1,1,1,0) v4 = (0,0,0,1)
x=(-i, 3i, 2-i, 1)
Алгебра и геометрия
Вариант 19
-
а) Доказать, что множество квадратных
 матриц из
матриц из
 ,
так что
,
так что
 ,
если
,
если
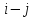 нечетно, с обычными операциями сложения
и умножения на числа является векторным
пространством над
нечетно, с обычными операциями сложения
и умножения на числа является векторным
пространством над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, у которых координаты
с четными номерами одинаковы. а) Доказать,
что
,
состоящее из строк, у которых координаты
с четными номерами одинаковы. а) Доказать,
что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (1,i,0,-1) v1 = (i,-i,1,1)
e2 = (i,-1,1,-i) v2 = (1,i,i,1)
e3 = (1,-i,1+i,1) v3 = (1+i,0,1,i)
e4 = (0,i,1,1) v4 = (0,i,-i,1)
x=(i, 1, -i, 1) i-номер варианта
Алгебра и геометрия
Вариант 20
-
а) Доказать, что все многочлены степени
 над
над
 ,
не содержащие четных степеней x
относительно обычных операций сложения
и умножения на числа, образуют векторное
пространство над
,
не содержащие четных степеней x
относительно обычных операций сложения
и умножения на числа, образуют векторное
пространство над
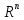 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк с нулевой суммой
первой и предпоследней координат. а)
Доказать, что
,
состоящее из строк с нулевой суммой
первой и предпоследней координат. а)
Доказать, что
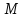 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
e1 = (1,0,0,0) v1 = (0,0,0,-1)
e2 = (0,0,1,0) v2 = (0,0,2,0)
e3 = (0,0,0,1) v3 = (1,0,0,0)
e4 = (0,1,0,0) v4 = (0,3,0,0)
x=(-i, 1+i, 1-i, 2)
Алгебра и геометрия
Вариант 1
-
а) Доказать, что множество матриц, у которых первая и последняя строка одинаковы, с обычными операциями сложения и умножения на числа является векторным пространством над
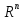 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, у которых сумма
первых двух и последних двух координат
равна нулю. а) Доказать, что
,
состоящее из строк, у которых сумма
первых двух и последних двух координат
равна нулю. а) Доказать, что
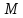 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и x
заданы своими координатами в некотором
базисе пространства
и x
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
 =
(1,i,0,-1)
=
(1,i,0,-1)
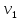 =(i,-i,1,1)
=(i,-i,1,1)
 =
(i,-1,1,-i)
=
(i,-1,1,-i)
 =(1,i,i,1)
=(1,i,i,1)
 =
(1,-i,1+i,1)
=
(1,-i,1+i,1)
 =(1+i,0,1,i)
=(1+i,0,1,i)
 =
(0,
i,
1,
1)
=
(0,
i,
1,
1)
 =(0,i,-i,1)
=(0,i,-i,1)
 =
(i,
1,
-i,
1)
=
(i,
1,
-i,
1)
Алгебра и геометрия
Вариант 2
-
а) Доказать, что множество симметричных квадратных
 матриц с вещественными элементами с
обычными операциями сложения и умножения
на числа образует векторное пространство
над
матриц с вещественными элементами с
обычными операциями сложения и умножения
на числа образует векторное пространство
над
 ;
б)
найти его базис и размерность.
;
б)
найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
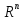 ,
состоящее из строк, у которых координаты
с нечетными номерами одинаковы. а)
Доказать, что
,
состоящее из строк, у которых координаты
с нечетными номерами одинаковы. а)
Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
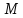 .
. -
Векторы
 и
и
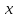 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
 =
(1,1,1,1)
=
(1,1,1,1)
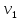 =(1,0,0,0)
=(1,0,0,0)
 =
(0,1,1,1)
=
(0,1,1,1)
 =(0,1,0,0)
=(0,1,0,0)
 =
(0,0,1,1)
=
(0,0,1,1)
 =(0,0,1,0)
=(0,0,1,0)
 =
(0,0,0,1)
=
(0,0,0,1)
 =(0,0,0,1)
=(0,0,0,1)
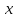 =
(1,
i,
2,
1+i)
=
(1,
i,
2,
1+i)
Алгебра и геометрия
Вариант 3
-
а) Доказать, что множество кососимметричных вещественных квадратных
 матриц с обычными операциями сложения
и умножения на числа образует векторное
пространство над
матриц с обычными операциями сложения
и умножения на числа образует векторное
пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, у которых все четные
координаты равны нулю. а) Доказать, что
,
состоящее из строк, у которых все четные
координаты равны нулю. а) Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
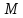 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
 =(1,2,3,4)
=(1,2,3,4)
 =(1,1,1,1)
=(1,1,1,1)
 =(2,3,1,2)
=(2,3,1,2)
 =(0,1,1,1)
=(0,1,1,1)
 =(1,1,1,-1)
=(1,1,1,-1)
 =(0,0,1,1)
=(0,0,1,1)
 =(1,0,-2,-6)
=(1,0,-2,-6)
 =(0,0,0,1)
=(0,0,0,1)
 =(i,
1, 2i,
1+i)
=(i,
1, 2i,
1+i)
Алгебра и геометрия
Вариант 4
-
а) Доказать, что множество всех верхнетреугольных матриц с действительными элементами и обычными операциями сложения и умножения на числа образует векторное пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
 ,
состоящее из строк, у которых все
нечетные координаты равны нулю. а)
Доказать, что
,
состоящее из строк, у которых все
нечетные координаты равны нулю. а)
Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
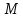 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
 =(1,1,0,0)
=(1,1,0,0)
 =(1,1,1,1)
=(1,1,1,1)
 =(0,1,1,0)
=(0,1,1,0)
 =(0,1,1,1)
=(0,1,1,1)
 =(0,0,1,1)
=(0,0,1,1)
 =(0,0,1,1)
=(0,0,1,1)
 =(0,0,0,1)
=(0,0,0,1)
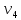 =(0,0,0,1)
=(0,0,0,1)
 =(i,
-1,
1,
2+i)
=(i,
-1,
1,
2+i)
Алгебра и геометрия
Вариант 5
-
а) Доказать, что множество всех многочленов f степени ≤ n с коэффициентами из
 ,
для которых 2f(0) = f(1) относительно обычных
операций сложения и умножения на числа,
образуют
векторное пространство над
,
для которых 2f(0) = f(1) относительно обычных
операций сложения и умножения на числа,
образуют
векторное пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
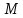 – подмножество в
– подмножество в
 ,
состоящее из строк, с двумя одинаковыми
последними координатами. а) Доказать,
что
,
состоящее из строк, с двумя одинаковыми
последними координатами. а) Доказать,
что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
 =(1,2,3,4)
=(1,2,3,4)
 =(1,1,1,1)
=(1,1,1,1)
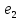 =(0,1,2,3)
=(0,1,2,3)
 =(0,1,1,1)
=(0,1,1,1)
 =(0,0,1,2)
=(0,0,1,2)
 =(0,0,1,1)
=(0,0,1,1)
 =(0,0,0,1)
=(0,0,0,1)
 =(0,0,0,1)
=(0,0,0,1)
 =(1,
2+i,
-i,
0)
=(1,
2+i,
-i,
0)
Алгебра и геометрия
Вариант 6
-
а) Доказать, что множество всех квадратных
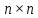 матриц с действительными элементами,
имеющих одинаковые числа на главной
диагонали с обычными операциями сложения
и умножения на числа образует векторное
пространство над
матриц с действительными элементами,
имеющих одинаковые числа на главной
диагонали с обычными операциями сложения
и умножения на числа образует векторное
пространство над
 ;
б) найти его базис и размерность.
;
б) найти его базис и размерность. -
Пусть
 – подмножество в
– подмножество в
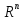 ,
состоящее из строк, сумма четных
координат которых, равна нулю. а)
Доказать, что
,
состоящее из строк, сумма четных
координат которых, равна нулю. а)
Доказать, что
 – подпространство в
– подпространство в
 ;
б) указать систему линейных уравнений,
определяющую
;
б) указать систему линейных уравнений,
определяющую
 ;
с) найти базу и размерность подпространства
;
с) найти базу и размерность подпространства
 .
. -
Векторы
 и
и
 заданы своими координатами в некотором
базисе пространства
заданы своими координатами в некотором
базисе пространства
 .
Доказать, что каждая из этих двух систем
является базисом в
.
Доказать, что каждая из этих двух систем
является базисом в
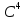 .
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
.
Найти матрицу перехода от первого
базиса ко второму и координаты вектора
 в обоих базисах.
в обоих базисах.
