4.3. Приложения двойного и тройного интегралов Примеры решения задач

1. Вычислить площадь фигуры D, ограниченной параболой

и прямой .

► Построим фигуру D:

Решив систему уравнений , получимсоответственно. Следовательно, линии, ограничивающие областьD, пересекаются в точках иМ(3;3).

Область D задается системой неравенств:

D: .

Тогда

◄

2. Найти объем тела Т, ограниченного цилиндрами ,и плоскостями.

► Данное тело Т ограничено сверху плоскостью , снизу плоскостью, по бокам прямыми цилиндрамии.

Изобразим тело Т и область интегрирования :

Переменная x изменяется от 0 до 4, т.е. ; при любом значении из этого промежутка. Кроме того,.

Итак,

.◄

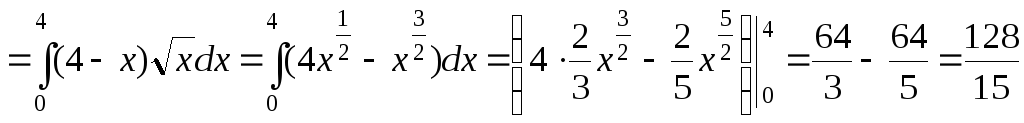3. Найти координаты центра масс однородной пластинки, ограниченной линиями ; плотность.

► Координаты центра масс иплоской фигуры D с плотностью вычисляются по формулам:

, (5.4)

гдеm − масса пластинки, иее статические моменты относительно осей координатисоответственно. В случае однородной пластинки эти формулы принимают вид

,

где S − площадь области D.

Найдем площадь S пластинки.

.

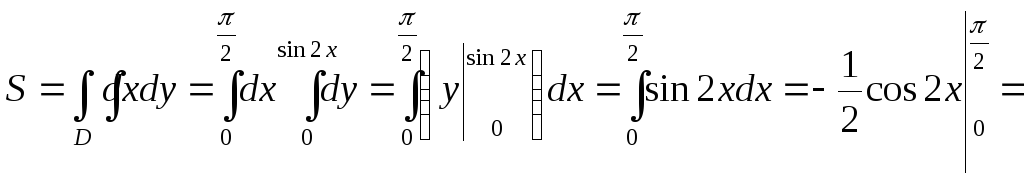
Вычислим статические моменты:

.◄

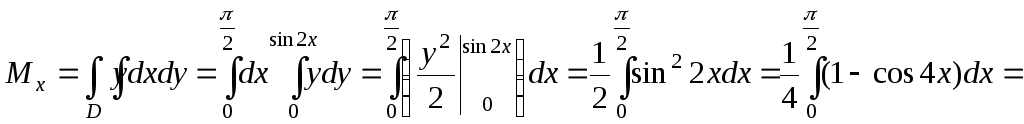
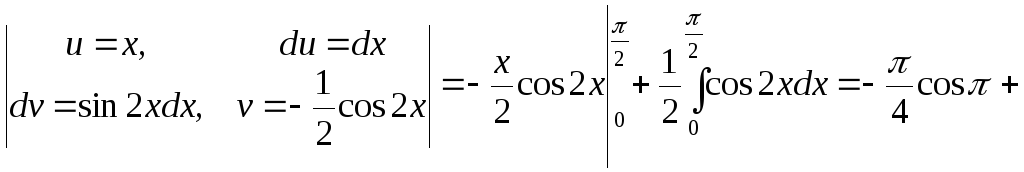
Таким образом, центр масс имеет координаты:

◄

4. Найти моменты инерции однородной фигуры (плотность =const), ограниченной линиями , относительно осейии начала координат.

► Данная фигура D изображена на рисунке и представляет собой треугольник с вершинами А (1; -1), В (1; 2) и С (-2; 2).

Моменты инерции иплоской фигуры с плотностьюотносительно осейивычисляются по формулам:

(4.5)

;

.

Момент инерции относительно начала координат вычисляем по формуле:

, (4.6)

следовательно, .◄

5. Найти объем тела, расположенного внутри цилиндра и ограниченного сферой.

► Объем тела выражается тройным интегралом вида

. (4.7)

В данном случае вычисления выполним в цилиндрических координатах. Уравнения поверхностей, ограничивающих тело, в цилиндрических координатах имеют следующий вид: − уравнение сферы,− уравнение цилиндра.

Таким образом, объем тела будет выражаться трехкратным интегралом

=.◄

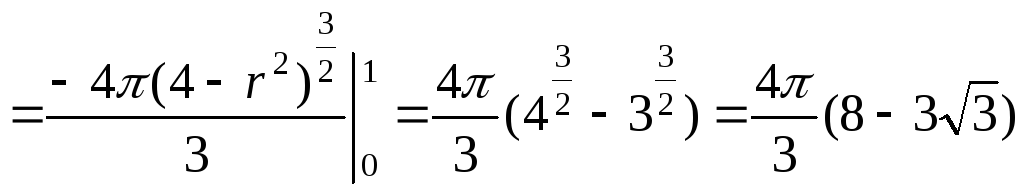Задания для самостоятельной работы

4.7. Вычислить площадь области D, ограниченной данными линиями, с помощью двойного интеграла:

1) ; 2);

3) ; 4);

5) .

4.8. Найти двойным интегрированием объемы тел, ограниченных указанными поверхностями:

1) плоскостями координат, плоскостями и параболоидом;

2) параболоидом вращения , координатными плоскостями и плоскостью;

3) цилиндром , координатными плоскостями и плоскостью

.

4.9. Найти координаты центра масс однородных фигур, ограниченных данными линиями:

1) 2);

3) ; 4).

4.10. Найти моменты инерции плоских фигур, ограниченных заданными функциями, относительно осей ии начала координат:

1) ;

2) ;

3) .

4.11. С помощью тройных интегралов вычислить объем тела:

1) ограниченного цилиндром и плоскостямии;

2) параболоида вращения, срезанного плоскостями и.

Тема 5. Криволинейные интегралы

5.1. Криволинейный интеграл первого рода по длине дуги. Примеры решения задач

1. Вычислить криволинейный интеграл первого рода , гдеL − дуга плоской кривой при.

► Найдем дифференциал длины дуги и применим формулу

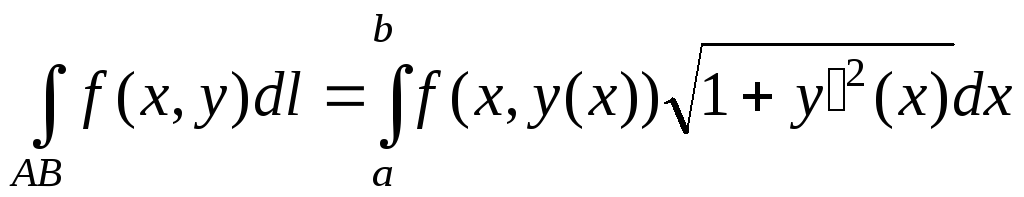(5.1)

.◄

2. Вычислить криволинейный интеграл первого рода , гдеL − первый виток конической винтовой линии

► Так как то

и по формуле вычисления криволинейного интеграла для кривой, заданной в параметрическом виде,

(5.2)

имеем

.◄

3. Вычислить криволинейный интеграл первого рода , гдеL − лепесток лемнискаты Бернулли , расположенной вI координатной четверти.

► Используем формулу

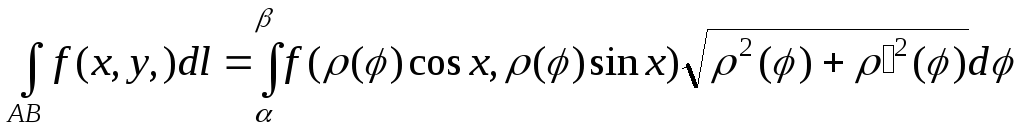, (5.3)

если кривая АВ задана в полярной системе координат.

; ;

.

В I координатной четверти полярная координата меняется от 0 до, тогда

.◄