Задания для самостоятельной работы
1.5. Найти интегралы от тригонометрических функций:
1)
; 2)
; 3)
;
4)
; 5)
; 6)
;
7)
; 8)
; 9)
;
10)
; 11)
; 12)
;
13)
.
1.4. Интегрирование иррациональных функций Примеры решения задач
Вычислить интегралы от иррациональных функций:
а)
; б)
;
в)
; г)
.
►а) Подстановкой
приведем интеграл к рациональному виду.
Тогда
.
б) Заметим, что
.
Применим
подстановку
,
откуда
;
.
Итак,
=
.
в) Выделяя полный квадрат в квадратном трехчлене под знаком корня, получаем:
.
Тогда, используя табличный интеграл 14, находим
.
г) Разобьем данный интеграл на сумму двух интегралов (в первом в числителе образуем производную от подкоренного выражения, а во втором выделим полный квадрат в подкоренном выражении):
.◄
Задания для самостоятельной работы
1.6. Найти интегралы от иррациональных функций:
1)
; 2)
;
3)
; 4)
;
5)
; 6)
;
7)
; 8)
;
9)
; 10)
;
11)
; 12)
.
Тема 2. Определенный интеграл.
2.1. Формула Ньютона-Лейбница.
Вычисление определенных интегралов
Примеры решения задач
.
Вычислить определенные интегралы, используя их свойства и формулу Ньютона-Лейбница:
а)
; б)
; в)
.
►Так как все подынтегральные функции непрерывны на соответствующих отрезках, то получаем:
а)
;
б) Под знаком интеграла неправильная дробь. Выделим целую часть, используя разложение
.
Имеем:
,
и данный интеграл
;
в)
.◄
2. Методом замены переменной вычислить определенные интегралы:
а)
; б)
; в)
.
а)
Введем новую переменную
.
Тогда
и новые пределы интегрирования
при
и
при
.
;
б)
;
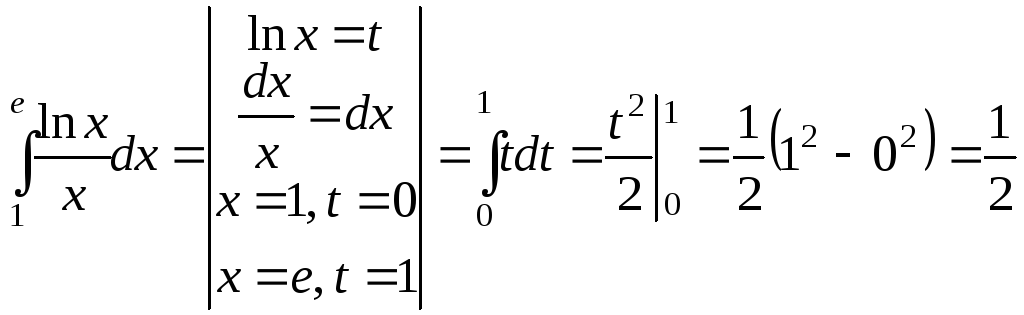в)
.◄
3. Используя формулу интегрирования по частям (1.4), вычислить следующие интегралы:
а)
; б)
.
►а)
.
б)
=
.◄
Вычислить интеграл
.
►Используем
подстановку
.
Тогда
при
,
при
и
.
К последнему интегралу применим интегрирование по частям:
◄
Задания для самостоятельной работы
2.1. Вычислить определенные интегралы по формуле Ньютона-Лейбница:
1)
; 2)
; 3)
;
4)
; 5)
; 6)
.
2.2. Используя формулу замены переменной, вычислить интегралы:
1)
; 2)
; 3)
;
4)
; 5)
; 6)
;
7)
; 8)
.
2.3. Вычислить интегрированием по частям следующие интегралы:
1)
; 2)
; 3)
;
4)
; 5)
; 6)
;
7)
; 8)
.
Приложения определенного интеграла
Примеры решения задач
1. Вычислить площадь
фигуры, ограниченной прямой
и кривой
.
►
Найдем
абсциссы точек пересечения данных
кривых:
Получим
.
Это и есть пределы интегрирования.
Тогда, по формуле
. (2.1)
находим площадь:
.◄
2
.
Вычислить площадь фигуры, ограниченной
лемнискатой
.
►Кривая задана в полярной системе координат.
Имеет место формула:
. (2.2)
Рис. 2
При
,
при
,
т.е.
.
Имеем
.◄
3. Вычислить объем
тела, полученного вращением вокруг оси
Оx
криволинейной
трапеции, ограниченной линиями
и осиОx.
►Для нахождения объема будем использовать формулу
.
В
пределах данной трапеции х
меняется от
0 до 2, значит,
.
Тогда
.◄
4. Найти длину дуги
кривой
,
заключенной между точками с абсциссами
и
.
►Для вычисления
длины дуги
применим формулу:
.
В
данном случае
,
.
Тогда
◄
5. Найти работу, затраченную на выкачивание жидкости из конического резервуара, обращенного вершиной вниз, если высота резервуара равна Н, радиус основания R.
►Вычислим вес элементарного слоя жидкости, находящейся на глубине х.
Высоту
этого слоя выберем таким образом, чтобы
сделать этот слой цилиндром радиуса
.
Тогда вес
этого слоя равен:
,
где
− плотность жидкости,
− ускорение свободного падения,
− объем цилиндра.
Из подобия треугольников АОD и СВD находим у:
.
Рис. 3
.
Элементарная работа, затраченная на поднятие этого слоя жидкости на высоту х, равна
,
поэтому
.◄
6. Найти силу давления воды на вертикальную стенку в форме полукруга, радиус которого R=3м.
►По закону Паскаля сила давления жидкости на площади вычисляется по формуле:
,
где
− плотность жидкости,
− ускорение силы тяжести,
− глубина погружения,
− площадь площадки.
О
бозначим
глубину погружения черезх.
Элементарную площадку будем считать
цилиндром радиуса
и высоты
.
Из треугольника
имеем:
.
Рис. 4
.
Найдем дифференциал давления на элементарную площадку:
.
Итак,
.◄