Распределение вероятности в выборках в зависимости от величины t и объема выборки n

n t	4	5	6	7	8	9	10	15	20	
0.5	0.348	0.356	0.362	0.366	0.368	0.370	0.372	0.376	0.378	0.383
1.0	0.608	0.626	0.636	0.644	0.650	0.654	0.656	0.666	0.670	0.683
1.5	0.770	0.792	0.806	0.816	0.832	0.828	0.832	0.846	0.850	0.865
2.0	0.860	0.884	0.908	0.908	0.914	0.920	0.924	0.936	0.940	0.954
2.5	0.933	0.946	0.955	0.959	0.963	0.966	0.968	0.975	0.978	0.988
3.0	0.942	0.960	0.970	0.976	0.980	0.938	0.984	0.992	0.992	0.997

Примечание

При оценке результатов малой выборки (численность которой не превышает 30 единиц), величина генеральной дисперсии в расчетах не используется. Величина и предельная ошибка малой выборки вычисляются на основе данных выборочного наблюдения:

и ,

где  мера случайных колебаний выборочной средней в малой выборке, а .

На заключительном этапе на основе предельной ошибки выборки определяют доверительные интервалы, в которых может находиться генеральная средняя или генеральная доля. Выход за пределы этой области имеет весьма малую вероятность. Доверительные интервалы определяются по формулам:

• для среднего значения: ;

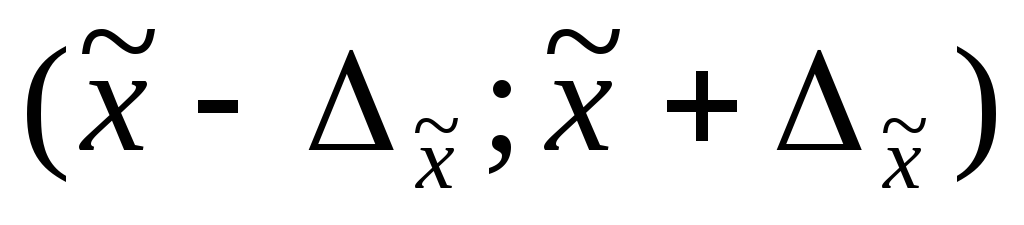• для доли: .

Типовая задача 1

Для анализа выполнения норм выработки предприятия было проведено 10%-ное механическое повторное выборочное обследование, результаты которого показали следующее распределение рабочих по выполнению норм выработки:

Группы рабочих по выполнению норм выработки, %	Число рабочих, чел.
1. до80 2. 80 – 90 3. 90 – 100 4. 100 – 110 5. более 110	5 19 25 36 15
Итого	100

Определить:

1) с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения норм выработки по предприятию;

2) с вероятностью 0.997 возможные пределы доли рабочих, выполняющих нормы выработки на 100% и более, в общей численности предприятия.

Решение

1) Определим возможные пределы среднего выполнения норм выработки по предприятию, т.е. доверительный интервал .

Сначала определим выборочную среднюю:

.

Т.к. отбор единиц в выборку по условию бесповторный, то определим величину предельной ошибки выборки по формуле:

, где

t = 2 (при p = 0,954);

n = 100 (чел.);

, т.к. по условию выборка 10%-ная, т.е. n составляет 10% от общей численности рабочих;

Получим .

Следовательно, определим границы доверительного интервала:

(98,7-2,1; 98,7+2,1)

(96,6; 100,8).

Таким образом, с вероятностью 0.954 можно утверждать, что среднее выполнение норм выработки по всему предприятию изменяется от 96,6 до 100,8%.

2) Определим возможные пределы доли рабочих, выполняющих нормы выработки сверх плана, т.е. доверительный интервал: .

Рассчитаем долю рабочих, выполняющих план на 100% и более. По условию таких рабочих 51 человек, значит:

или 51%.

Т.к. отбор единиц в выборку по условию бесповторный, то определим величину предельной ошибки выборки по формуле:

, где t = 3 (при p = 0,997), тогда получим

или 14%.

Определим границы доверительного интервала:

(51-14; 51+14)

(37; 65)

Таким образом, с вероятностью 0.997 можно утверждать, что доля рабочих, выполняющих план на 100% и более, в общей численности предприятия изменяется от 37 до 65%.

При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Для этого используют следующие формулы расчета (табл. 4.3).

Таблица 4.3

Вид выборочного наблюдения	Методы отбора
	Повторный отбор	Бесповторный отбор
Собственно-случайная и механическая выборка
для среднего значения
для доли
Типическая выборка
для среднего значения
для доли
Серийная выборка
для среднего значения
для доли

Отметим, что с увеличением предельной ошибки уменьшается необходимый объем выборки, и наоборот.