!Оптика и квантовая механика / Задачи / 11 / zan8

5.124

Свет с длиной волны падает нормально на длинную прямоугольную щель ширины . Найти угловое распределение интенсивности света при фраунгоферовской дифракции, а также угловое положение минимумов.

Решение:

Мысленно разобьем щель на множество одинаковых полосок и изобразим, имея ввиду первый рисунок, цепочку соответствующих элементарных векторов – для определенного угла дифракции . Если достаточно мал,

цепочка образует дугу радиуса R (второй рисунок). Пусть длина цепочки и результирующий вектор . Тогда как видно из второго рис , где разность фаз между крайними векторами цепочки. Исключив R из этих равенств получим

Отсюда интенсивность ()

,

Где интенсивность в центре дифракционной картины (=0), . С ростом угла увеличивается , и цепочка будет закручиваться. Когда цепочка замыкается один, два,… k раз, и мы приходим к условию , k=1,2…

5.125

Монохроматический свет падает нормально на щель ширины =11 мкм. За щелью находится тонкая линза с фокусым расстоянием =150 мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка (на экране) равно =50 мм.

Решение:

условие минимумов на щели

где угол под которым лучи выходят из щели. В нашем случае можно записать , надо найти . Из прямоугольного треугольника

=0,6 мкм.

5.126

Свет с диной волны =0,50 мкм падает на щель ширины =10 мкм под углом к её нормали. Найти угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.

Решение:

д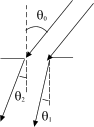ля минимума m=1 разность хода , для m= -1 . Отсюда =33, =27 градусов.

5.128

Монохроматический свет падает на отражательную дифракционную решетку с периодом d=1,0 мм под углом скольжения . Под углом скольжения образуется фраунгоферов максимум второго порядка. Найти длину волны света.

Решение:

найдем разность хода, она будет равно двум длинам волны, так как максимум второй. Итак разность хода

.

5.129

Изобразить примерную дифракционную картину, возникающую при дифракции Фраунгофера от решетки из трех одинаковых щелей, если отношение периода решетки к ширине щели равно: а) двум; б) трем.

а) Так как , то каждый второй максимум будет пропадать. Самый большой максимум – центральный, отсчет начинаем со следующего главного максимума. Количество побочных максимумов N-2, т.е. 1. Линия сверху, это график от одной щели.

б) Так как , то каждый 3 максимум будет пропадать. Количество побочных максимумов N-2, т.е. в нашем случае 1.

5.130

При нормальном падении света на дифракционную решетку угол дифракции для линии =0,65 мкм во втором порядке равен 45 градусов. Найти угол дифракции для линии =0,50 мкм в третьем порядке.

Решение: условие максимумов для решетки , отсюда находим, что .

5.131

Свет с длиной волны 535 нм падает нормально на дифракционную решетку. Найти ее период, если одному из фраунгоферовых максимумов соответствует угол дифракции 35 градусов и наибольший порядок спектра равен пяти.

Решение:

Условие максимума для решетки , k=1,2,3… У нас максимальный порядок равен 5, это значит (квадратные скобки-это целая часть). Отсюда можно заключить, что . Подставим угол 35 градусов и найдем какой максимум ему соответствует. , так как m это целое число, делаем вывод, что m=3. теперь подставим это в условие максимумов и найдем период решетки .

5.132

Определить длину волны монохроматического света, падающего нормально на дифракционную решетку с периодом , если угол между направлениями на фраунгоферовы максимумы первого и второго порядков .

Решение: условие максимумов для решетки

Отсюда находим . Раскладываем второе уравнение как синус суммы, получим

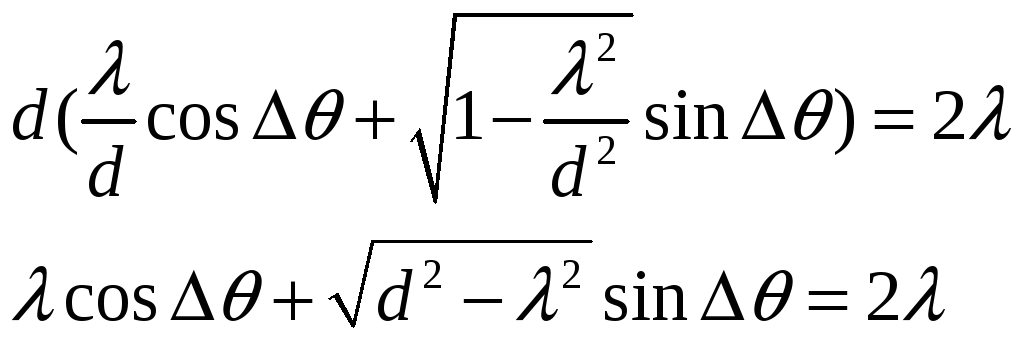
Переносим первое слагаемое вправо и возводим в квадрат

5.133

Свет с длиной волны 530 нм падает на прозрачную дифракционную решетку, период которой равен 1,50 мкм. Найти угол с нормалью к решетке, под которым образуется фраунгоферов максимум наибольшего порядка, если свет падает на решетку: а) нормально; б) под углом 60 градусов к нормали

Решение:

а) Максимальный порядок . Разность хода

б) запишем разность хода . Пинимая во внимание, то что максимальное значение это 1, получаем m=5.

.

№5.141

Свет с длиной волны падает на дифракционную решетку. Найти ее угловую дисперсию в зависимости от угла дифракции .

Решение:

Поскольку мы имеем дело с дифракционной решеткой, то запишем условие главных фраунгоферовых максимумов : .

Как известно угловая дисперсия дифракционной решетки:

Выразив отношение из первого уравнения и подставив его во второе, получим, что

■

№5.146

Свет падает нормально на дифракционную решетку ширины , имеющую 200 штрихов на миллиметр. Исследуемый спектр содержит спектральную линию с , которая состоит из двух компонент, отличающихся на . Найти:

А) в каком порядке спектра эти компоненты будут разрежены;

Б) наименьшую разность длин волн, которую может разрешить эта решетка в области .

Решение:

А) Как известно, разрешающая способность , также мы знаем, что для дифракционной решетки , где -кол-во штрихов решетки, - порядок спектра.

Определим сколько штрихов у нашей решетки: , где кол-во штрихов на миллиметр.

Тогда окончательно для получаем: ■

Б) Мы знаем, что разрешающая способность .

Для нахождения минимальной разности длин волн, которую может разрешить эта решетка, нам надо найти максимальный порядок спектра, что мы сделаем из условия максимума на решетке:

, возьмем

Тогда для получаем, что ■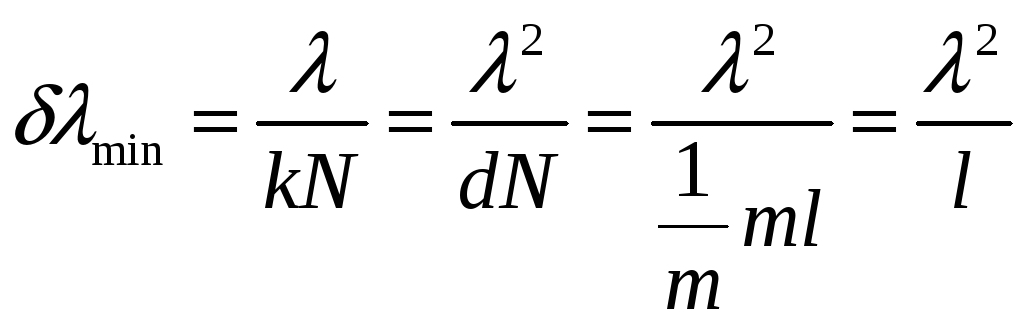

(здесь мы воспользовались тем, что период решетки )

№5.147

При нормальном падении света на дифракционную решетку ширины 10мм обнаружено, что компоненты желтой линии натрия (589.0 и 589.6 нм) оказывается разрешенными, начиная с пятого порядка спектра. Оценить:

А) период этой решетки;

Б) при какой ширине решетки с таким же периодом можно разрешить в третьем порядке дублет спектральной линии с , компоненты которого отличаются на 0.13нм.

Решение:

Пусть как и прежде - это количество штрихов на миллиметр, тогда разрешающая способность

, где -ширина решетки.

Мы знаем, что период решетки ■

Б) Воспользуемся, найденным значением из первого пункта, после чего легко получаем, что

■