!Оптика и квантовая механика / Задачи / 11 / zan25

Занятие 25.

№ 6.177.

Определить угловую скорость вращения молекулы , находящейся на первом возбужденном вращательном уровне.

Решение:

По определению ротационной энергии,

.

С другой стороны, из классической механики,

,

тогда

.

Т.к. молекула находится на первом возбужденном вращательном уровне (первому возбужденному вращательному уровню соответствует ),

,

причем здесь - приведенная масса молекулы серы:

,

где - масса атома серы. Тогда масса молекулы серы , тогда

,

где - масса молекулы серы. 

№ 6.178.

Найти для молекулы вращательные квантовые числа двух соседних уровней, разность энергий которых мэВ.

Решение:

При вращательных спектрах излучается фотон, частота которых определяется изменениями только во вращательном состоянии:

,

причем . Подставив это в выражение выше, получим:

, ,

где - приведенная масса молекулы, - расстояние между ядрами. Для молекулы :

кг.

.

.

3; . 

№ 6.189.

В середине колебательно-вращательной полосы спектра испускания молекул , где отсутствует «нулевая» линия, запрещенная правилом отбора, интервал между соседними линиями . Вычислить расстояние между ядрами молекулы .

Решение:

Колебательно-вращательный спектр можно описать формулой

,

где Колебательно-вращательная полоса изображена на рисунке. Очевидно,

.

Отсюда можно найти расстояние между ядрами молекул:

,

где - приведенная масса молекулы . 

№ 6.190.

Вычислить длины волн красного и фиолетового спутников, ближайших к несмещенной линии, в колебательном спектре комбинационного рассеяния молекул , если длина волны падающего света нм.

Решение:

Запишем закон сохранения энергии. До взаимодействия – энергия падающего фотона и колебательная энергия, после взаимодействия – энергия излученного фотона и измененная колебательная энергия:

.

Здесь , . Поскольку правилом отбора разрешены только переходы ,

.

Тогда после сокращения всего уравнения на , получим:

,

где - частота колебаний молекулы фтора (табличное значение). Итак,

. 

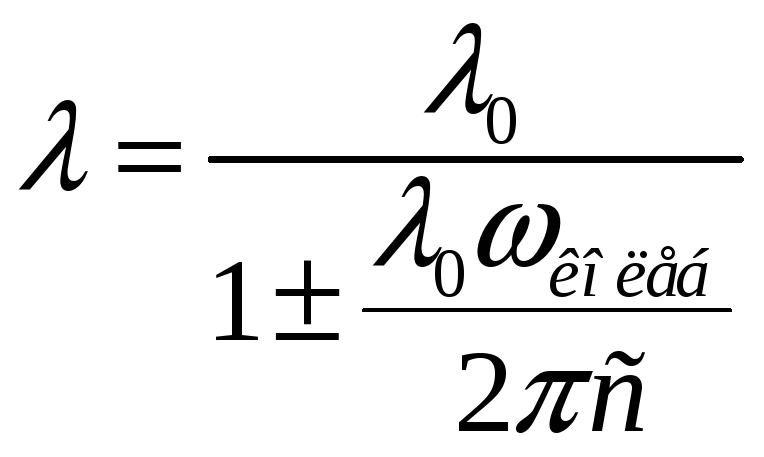№ 6.182.

Найти для молекулы число вращательных уровней, расположенных между нулевым и первым возбужденным колебательными уровнями, считая вращательные состояния не зависящими от колебательных.

Решение:

