Лекции по дискретной математике / Лекция 4.Комбинаторика (прод)

4. Комбинаторика (продолжение).

4.6. Перестановки с повторениями.

Иногда требуется переставлять предметы, некоторые из которых неотличимы друг от друга. Рассмотрим такой вариант перестановок, который называется перестановками с повторениями.

Пусть имеется n₁ предметов 1-го типа, n₂ предмета 2-го, n_k пред­метов k-го типа и при этом n₁ + n₂ + … + n_k = n. Количество разных перестановок предметов:

(5)

Для обоснования сначала будем переставлять n предметов в предположении, что они все различны. Число таких перестановок равно n!

Затем заметим, что в любой выбранной перестановке пере­становка n₁ одинаковых предметов не меняет комбинации, аналогично перестановка n₂ одинаковых предметов также не меняет комбинации и т. д. Поэтому получаем выражение (5).

Задача. Сколькими способами можно расставить белые фигуры на первой линии шахматной доски?

Решение. На первой линии могут находиться король, ферзь, 2 ладьи, 2 коня и 2 слона. Без учета общепринятых шахматных правил образуются кортежи длины 8, имеющие указанный состав (1, 1, 2, 2, 2). Тогда число перестановок с размещениями найдем по формуле (5):

Задача. Сколько разных слов можно составить из всех букв слова МАТЕМАТИКА?

Решение. Имеем следующее количество разных букв: М – 2, А – 3, Т – 2, Е – 1, И – 1, К – 1. Всего 10 букв.

Т.о., образуются кортежи длины 10, имеющие указанный состав (2, 3, 2, 1, 1, 1). Число перестановок с размещениями найдем по формуле (5):

Задача. В магазине продается 4 сорта пирожных: бизе, эклеры, песочные, наполеоны. Сколькими способами можно выбрать 7 пирожных?

Решение. Каждая покупка – это выборка из 4 элементов по 7, причем с повторениями, так как 4 < 7. Порядок следования сорта пирожных внутри выборки не важен. Следовательно, число таких покупок равно числу всех сочетаний с повторениями:

Задача. У врача 3 таблетки одного лекарства, 2 таблетки – другого и 4 таблетки – третьего. Сколькими способами он может распределить прием имеющихся таблеток по одной в день?

Решение. Порядок приёма таблеток важен. Есть повторяющиеся таблетки. Общее число таблеток 3 + 2 + 4 = 9 равно числу дней приема лекарств. Решение задачи сводится к нахождению числа всех перестановок с повторениями из 9 элементов:

Задача. Сколько различных слов можно получить перестановкой букв слова огород так, чтобы три буквы "о" не стояли бы рядом?

Решение. Общее количество различных слов, полученных перестановкой букв слова огород, равно

Если в каком-то слове все три буквы "о" стоят рядом, то тройную "о" можно считать единым символом, и количество слов, в которых три буквы "о" стоят рядом, равно Р(4) = 4! =24.

В итоге получаем: 120 - 24 = 96.

Задача. Найти разложение (a+b)⁶, используя треугольник Паскаля.

Решение.

Задача. Написать разложение бинома (x–2y)⁵.

Решение.

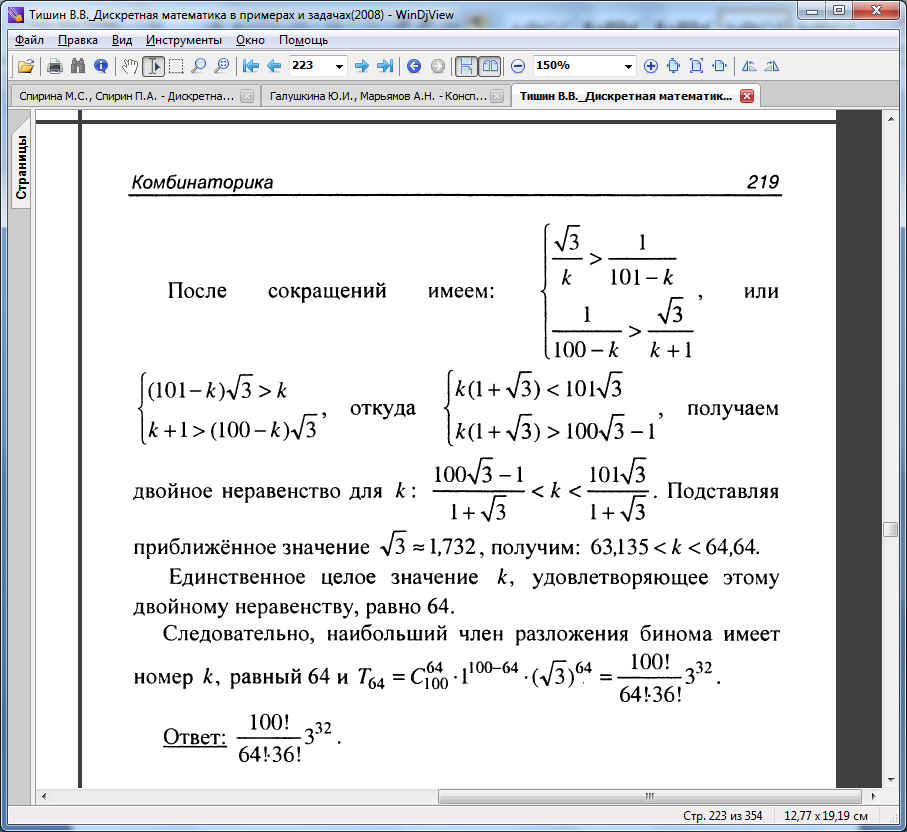
Задача. Найти наибольший член разложения бинома .

Решение.

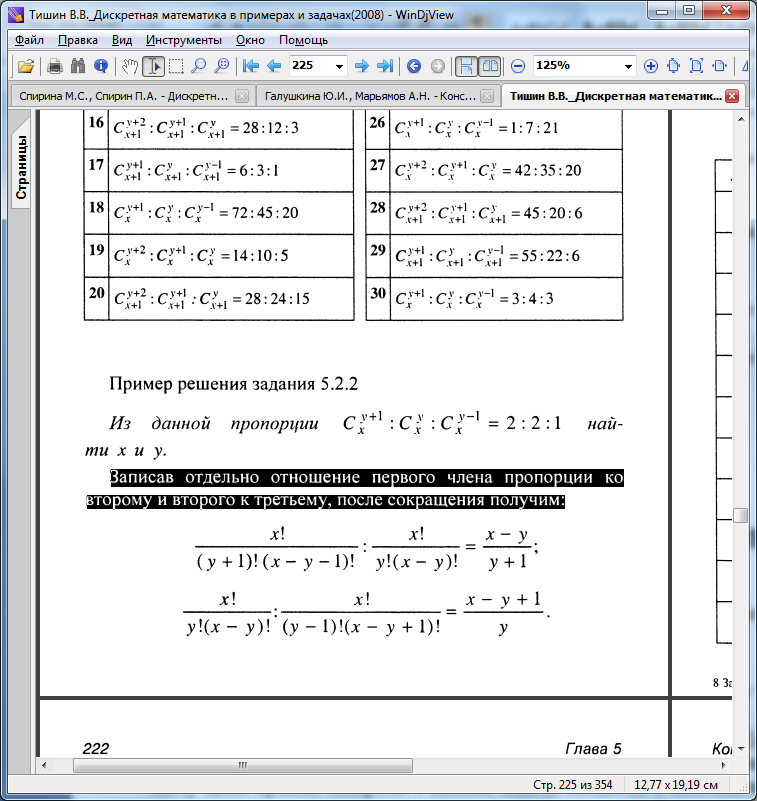
Задача. Из данной пропорции найти x и y.

Решение.

Записав отдельно отношение первого члена пропорции ко второму и второго к третьему, после сокращения получим:

В силу условия задачи мы приходим к системе:

Решая её, получаем x=5 и y=1.