
- •Комбинаторика – раздел дискретной математики, посвящённый решению задач выбора и расположения элементов некоторого,
- •Понятие выборки отличается от понятия подмножества:
- •Упорядоченная (n, k)– выборка без повторений
- •Правило суммы гласит, что если А и В -несвязанные события, и существует n1
- •Правило суммы
- •Очень многие комбинаторные задачи решаются применением трех простых правил: равенства, суммы и произведения.
- •Правило суммы – частный случай формулы включений и исключений. Если рассматривать А и
- •Задача 4. Сколько существует двузначных четных чисел с разными цифрами?
- •Задача 5. Сколько существует четырехзначных чисел, делящихся на 5, у которых все цифры
- •Эту же задачу можно решить другим способом.
- •А –первая буква французского слова arrangement, что означает размещение, приведение в порядок
- •Задача 5. Сколько различных четырехбуквенных «слов» можно составить , используя буквы f,c,o,n,e, если
- •P – первая буква французского слова
- •ПРИМЕР: Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они
- •Размещение с повторениями из n элементов множества M по k - это всякая
- •Сколькими способами из колоды в 36 карт можно вытащить 5 карт так, чтобы
- •СОЧЕТАНИЯ с повторениями.
- •Есть n ящиков, в которых размещается k шариков.
- •-размещение 9 шариков по 7 ящикам.
- •И еще один:
- •Задача. В магазине продается 4 сорта пирожных: бизе, эклеры, песочные, наполеоны. Сколькими способами
- •Основные свойства сочетаний
- •Перестановки с повторениями
- •Число элементов в каждой перестановке равно
- •Например, в перестановке «ммаа» ничего не изменится, если переставит первый элемент со вторым,
- •ПРИМЕР:
- •Задача. У врача 3 таблетки одного лекарства, 2 таблетки – другого и 4
- •Задача. Сколько различных слов можно получить перестановкой букв слова ОГОРОД так, чтобы три
- •Найти количество перестановок букв в слове КОЛОБОК .

Есть n ящиков, в которых размещается k шариков.
Нас интересует только количество шариков в каждом ящике. То есть результатом эксперимента является набор чисел
k1, k2 |
|
, в котором |
ki |
— число шариков в ящике с |
|
,..., kn |
|
|
|||
номером |
i , и |
|
|
||
|
|
k1 |
... kn |
k |
|
Числа |
ki |
принимают натуральные значения или равны 0. |
|||
Изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а кружки — находящиеся в ящиках шарики:
45

-размещение 9 шариков по 7 ящикам.
-Здесь 1-й ящик содержит 3 шарика, 2-й и 6-й ящики пусты, 3-й и 7-й ящики содержат по одному шарику, и в 4- м и 5-м ящиках есть по 2 шарика.
-Переложим один шарик из первого ящика во второй и изобразим таким же образом еще один результат размещения:
46

И еще один:
Получим, что все размещения можно получить, меняя между собой шарики и перегородки, или расставляя k шариков на n-1+k месте.
Число n-1+k получается так: у n ящиков есть ровно n+1 перегородка, считая крайние,
или n-1 перегородка, если не считать крайние, которые двигать нельзя.
И есть k шариков.
Перебрав все возможные способы расставить k шариков на этих n-1+k местах (и ставя на оставшиеся места перегородки), переберем все нужные размещения.
47

Но способов расставить k шариков на n-1+k местах ровно Сnk 1 k— это в точности число способов выбрать из
n-1+k номеров мест k номеров мест
(без учета порядка и без повторения), на которые нужно поместить шарики.
Общее количество выборок в схеме выбора
k элементов из n с повторением и без учета порядка определяется формулой
Cnk Сnk k 1 Cnn 1k 1
48

Задача. В магазине продается 4 сорта пирожных: бизе, эклеры, песочные, наполеоны. Сколькими способами можно выбрать 7 пирожных?
Решение. Каждая покупка – это выборка из 4 элементов по 7, причем с повторениями, так как 4 < 7.
Порядок следования сорта пирожных внутри выборки не важен. Следовательно, число таких покупок равно числу всех сочетаний с повторениями:
|
|
|
|
10! |
|
8 9 10 120. |
|
C7 |
C7 |
||||||
|
|||||||
4 |
10 |
|
7!3! |
1 2 3 |
|||
|
|
|
|
||||

Основные свойства сочетаний |
|
|||
1. |
m |
n m |
ФОРМУЛА |
|
|
|
|||
Сn |
Cn |
СИММЕТРИИ |
||
|
|
|
||
2. |
m |
m 1 |
m 1 |
ФОРМУЛА |
Cn |
Cn |
Cn 1 |
СЛОЖЕНИЯ |
|
|
|
|
|
|
n
3. Сnk 2n
k 0
ЧИСЛО ВСЕХ ПОДМНОЖЕСТВ N-ЭЛЕМЕНТНОГО МНОЖЕСТВА
50

Ak |
|
k |
С |
||
n |
n |
|
Ank |
k |
|
|
Сn |
51

Перестановки с повторениями
Число различных перестановок, которые можно построить из n элементов, среди которых находятся n1 - элементов первого типа,
n2 - элементов второго типа,…, nk - элементов k-го типа равно
P(n1, n2 ,.., nk ) n! n1!n2!...nk !
n1 n2 nk n
52
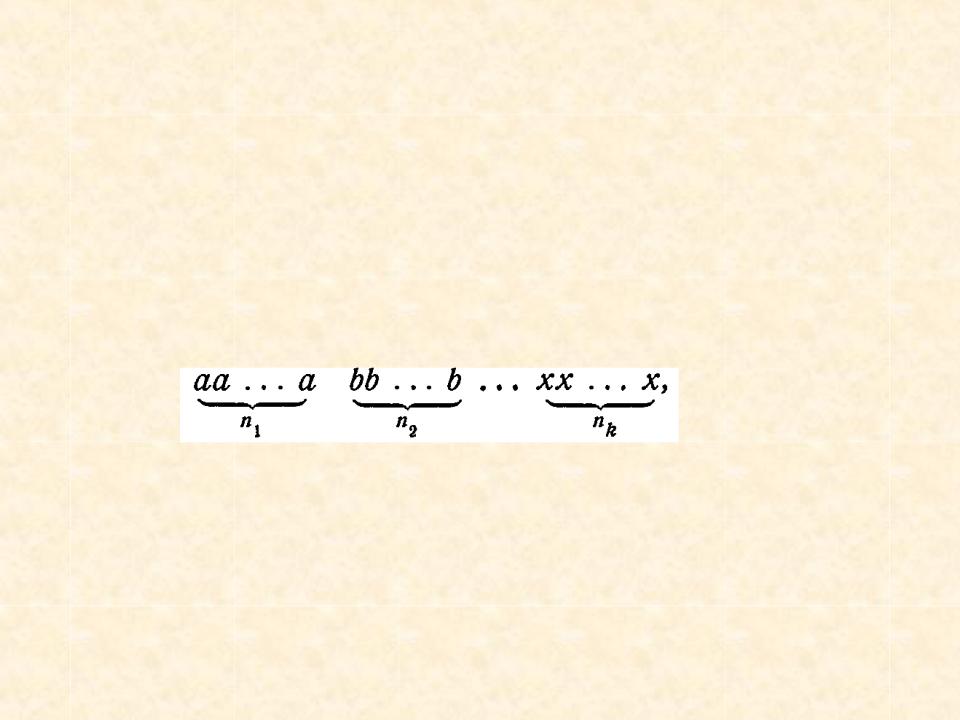
Число элементов в каждой перестановке равно
n1 n2 nk n
Поэтому если бы все элементы были различны,
то число перестановок равнялось бы n! . Но из-за того, что
некоторые элементы совпадают, получится меньшее число перестановок. Возьмем перестановку
В которой сначала выписаны все элементы первого типа, потом все элементы второго типа,…,наконец, все элементы k-го типа. Элементы первого типа можно переставлять с друг другом n1! способами. Но так как все эти элементы одинаковы, то такие перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок второго типа и т.д. 53

Например, в перестановке «ммаа» ничего не изменится, если переставит первый элемент со вторым, или третий с четвертым.
Перестановки элементов первого типа, второго типа и т.д. можно делать независимо друг от друга. Поэтому по правилу произведения элементы нашей перестановки
можно переставлять друг с другом |
n1 n21 nk ! |
способами так, что она остается |
неизменной. То же |
самое верно и для любого другого расположения элементов.
Поэтому множество всех n! перестановок распадается на части, состоящие из одинаковых перестановок каждая. Значит число различных перестановок с повторениями, которые можно сделать из данных
элементов равно |
P(n1, n2 |
,.., nk ) |
n! |
|
|
n1!n2!...nk ! |
|||
|
54 |
|
||
|
|
|
|
|

55
