
- •Глава I.
- •§1.1. Матрицы и операции над ними.
- •§1.2. Определители. Теорема Лапласа.
- •§1.3. Теоремы о произведении определителей и обратной матрице. Правило Крамера.
- •Глава II. Линейные пространства и
- •§2.1. Арифметическое линейное пространство .
- •§2.2. Ранг матриц.
- •§2.3. Системы линейных уравнений.
- •Глава 3.
- •§3.1. Матрицы линейных операторов.
- •§3.2. Ранг и дефект линейного оператора.
- •§3.3. Характеристические корни и собственные значения.
- •Глава 4.
- •§4.1. Группы, кольца, поля.
- •§4.2. Поле комплексных чисел.
- •§4.3. Поля вычетов.
- •§4.4. Кольца многочленов.
- •Глава I. Матрицы и определители. 5
Глава 3.
ЛИНЕЙНЫЕ ОПЕРАТОРЫ.
§3.1. Матрицы линейных операторов.
Пусть
дано множество
![]() ;
его
элементы будут обозначаться малыми
латинскими буквами:
;
его
элементы будут обозначаться малыми
латинскими буквами:
![]() Пусть,
далее, в множестве
Пусть,
далее, в множестве
![]() определены
операция
сложения, ставящая
в соответствие всякой
паре элементов
определены
операция
сложения, ставящая
в соответствие всякой
паре элементов
![]() из
из
![]() однозначно
определенный элемент
однозначно
определенный элемент
![]() из
из
![]() ,
называемый
их суммой,
и
операция
умножения
на
действительное число, причем
произведение
,
называемый
их суммой,
и
операция
умножения
на
действительное число, причем
произведение
![]() элемента
элемента![]() на
число
на
число
![]() ,
однозначно определено и принадлежит
к
,
однозначно определено и принадлежит
к
![]() .
.
Элементы
множества
![]() будут
называться векторами,
а
само
будут
называться векторами,
а
само
![]() действительным
линейным
(или
векторным,
или
аффинным)
пространством, если
указанные операции обладают свойствами
действительным
линейным
(или
векторным,
или
аффинным)
пространством, если
указанные операции обладают свойствами
![]() из§2.1.
Так, арифметическое
из§2.1.
Так, арифметическое
![]() мерное векторное пространство является
примером линейного пространства.
мерное векторное пространство является
примером линейного пространства.
Два
линейных пространства
![]() и
и![]() называютсяизоморфными,
если существует биективное отображение
называютсяизоморфными,
если существует биективное отображение
![]() ,
ставящее в соответствие каждому вектору
,
ставящее в соответствие каждому вектору![]() пространства
пространства![]() вектор
вектор![]() пространства
пространства![]() ,
такое что:
,
такое что:
![]()
Пусть
![]() базис
базис
![]() и
и
![]() .
Так как
.
Так как
![]() система порождающих, то найдутся числа
система порождающих, то найдутся числа![]() такие, что
такие, что![]() .
Если также
.
Если также![]() ,
то имеем
,
то имеем![]() .
Но
.
Но![]() линейно независимая система, откуда
линейно независимая система, откуда![]() .
Значит
.
Значит![]() .
Итак, представление вектора
.
Итак, представление вектора![]() в виде линейной комбинации базисных
векторов возможно и единственно. Набор
(
в виде линейной комбинации базисных
векторов возможно и единственно. Набор
(![]() )
называетсякоординатами
вектора х
в базисе
)
называетсякоординатами
вектора х
в базисе
![]() .
.
Отображение
![]() называетсялинейным
оператором,
если выполнены условия: для всех
называетсялинейным
оператором,
если выполнены условия: для всех
![]() и числа
и числа
![]() :
:
(а)
![]()
(б)
![]() ,
,
которые можно
заменить одним: для всех
![]() и чисел
и чисел
![]() верно
верно![]() .
Отсюда следует равенство
.
Отсюда следует равенство
![]() ,
,
широко используемое в дальнейшем.
Справедлива следующая
ТЕОРЕМА (о
существовании и единственности
![]() ).
Пусть
).
Пусть![]() базис
базис
![]() и
и
![]() произвольные векторы из
произвольные векторы из
![]() .
Тогда существует единственный линейный
оператор
.
Тогда существует единственный линейный
оператор
![]() такой, что
такой, что![]() .
.
ДОКАЗАТЕЛЬСТВО.
Если
![]() ,
то зададим
,
то зададим![]() так:
так:![]() .
Проверим, что
.
Проверим, что
![]() линейный оператор. Если
линейный оператор. Если
![]() и
и![]() произвольные числа, то
произвольные числа, то
Предположим, что
![]() также линейный оператор
также линейный оператор
![]() ,
причем
,
причем
![]() .
.
Имеем
![]() .
Итак
.
Итак![]() для любого
для любого![]() .
Значит
.
Значит![]() .
□
.
□
Доказанная теорема
показывает, что линейный оператор
однозначно определяется в данном базисе
![]() своими значениями
своими значениями
![]() .
Приходим к определению:матрицей
линейного оператора
.
Приходим к определению:матрицей
линейного оператора
![]() в базисе
в базисе![]() называется такая матрица
называется такая матрица
![]()
![]() ,
у которой
,
у которой![]() столбец есть координаты вектора
столбец есть координаты вектора![]() в базисе
в базисе
![]() .
Т. е.,
.
Т. е.,
 .
.
Обозначим через
![]() столбец из координат
вектора
столбец из координат
вектора
![]() в базисе
в базисе
![]() ,
т.е.
,
т.е.
 .
В частности,
.
В частности,![]() столбец
из координат вектора
столбец
из координат вектора![]() в этом же базисе.
в этом же базисе.
Имеет место следующее равенство
![]() (1)
(1)
Действительно,
![]()
Но в последней
сумме коэффициенты при
![]() как раз есть координаты вектора
как раз есть координаты вектора
![]() в базисе
в базисе
![]() .
Из правила умножения матрицы
.
Из правила умножения матрицы
![]() на столбец
на столбец![]() получаем искомое
равенство (1). □
получаем искомое
равенство (1). □
Пусть
![]() другой базисL.
Матрицей
перехода от одного базиса
другой базисL.
Матрицей
перехода от одного базиса
![]() к другому
к другому
![]() называется такая матрица
называется такая матрица![]() ,
у которойi-ый
столбец есть координаты вектора
,
у которойi-ый
столбец есть координаты вектора
![]() в базисе
в базисе![]() ,
т. е.
,
т. е.

Фактически матрица
![]() есть матрица линейного оператора,
переводящего векторы
есть матрица линейного оператора,
переводящего векторы![]() в
в![]() .
.
Пусть
 столбец из координат вектора
х в базисе
столбец из координат вектора
х в базисе
![]() Тогда имеет место следующее равенство
Тогда имеет место следующее равенство
![]() (2)
(2)
Действительно, имеем
![]()
Но
![]() откуда
откуда
![]()
Но в последней
сумме коэффициенты при
![]() как раз и есть координаты векторах
в базисе
как раз и есть координаты векторах
в базисе
![]() .
Из правила умножения матрицы
.
Из правила умножения матрицы![]() на столбец
на столбец![]() получаем (2).
получаем (2).
По следствию 2 из
теоремы о ранге матриц
![]() невырожденная матрица, т.к. её столбцы,
будучи координатами базисных векторов
линейно независимы. ПоэтомуТ
имеет обратную матрицу
невырожденная матрица, т.к. её столбцы,
будучи координатами базисных векторов
линейно независимы. ПоэтомуТ
имеет обратную матрицу
![]() .
Умножая обе части равенства (2) слева
на
.
Умножая обе части равенства (2) слева
на![]() ,
получаем
,
получаем
![]()
Пример 1.
Векторы
![]() заданы своими координатами в некотором
базисе
заданы своими координатами в некотором
базисе![]() .
Показать, что векторы
.
Показать, что векторы![]() сами образуют базис, и найти координаты
вектораx
в этом базисе.
сами образуют базис, и найти координаты
вектораx
в этом базисе.
Решение.
Составим матрицу перехода от базиса
![]() к системе векторов
к системе векторов![]() :
:
 ,
,
она невырожденная,
значит векторы
![]() линейно независимы и могут образовывать
базис трёхмерного пространства. Тогда
линейно независимы и могут образовывать
базис трёхмерного пространства. Тогда

Найдём координаты
вектора
![]() в
базисе
в
базисе![]()

Следующая теорема устанавливает связь между матрицами одного и того же линейного оператора, заданными в разных базисах.
ТЕОРЕМА (о связи
матриц линейного оператора).
Пусть
![]() и
и![]() – матрицы линейного оператора
– матрицы линейного оператора![]() в базисах
в базисах![]() и
и![]() соответственно и
соответственно и![]() матрица перехода о первого базиса ко
второму. Тогда
матрица перехода о первого базиса ко
второму. Тогда![]() (матрицы
(матрицы![]() и
и![]() называются подобными).
называются подобными).
ДОКАЗАТЕЛЬСТВО.
Если
![]() ,
то обозначим через
,
то обозначим через![]() и
и![]() столбцы из координат вектора
столбцы из координат вектора![]() в первом и во втором базисах, а через
в первом и во втором базисах, а через![]() и
и![]() координаты образа этого вектора в
первом и во втором базисах.. Из равенства
(2) имеем
координаты образа этого вектора в
первом и во втором базисах.. Из равенства
(2) имеем
![]()
Из равенства (1) получаем
![]() и
и
![]() .
.
Из этих трех равенств заключаем, что
![]() .
.
Но
![]() откуда
откуда
![]() .
.
Домножая обе части
этого равенства на
![]() слева, получаем равенство
слева, получаем равенство
![]()
Которое имеет
место при любом векторе
![]() .
Это означает равенство матриц
.
Это означает равенство матриц![]() и
и![]() .□
.□
В доказательстве
теоремы молчаливо использовался тот
факт, что если для любого вектора х
выполнено
![]() ,
то
,
то![]() .
Предлагается его доказать читателю.
.
Предлагается его доказать читателю.
Пример 2. Линейный
оператор
![]() в базисе
в базисе![]() имеет матрицу
имеет матрицу .
Найти его матрицу
.
Найти его матрицу![]() в базисе
в базисе
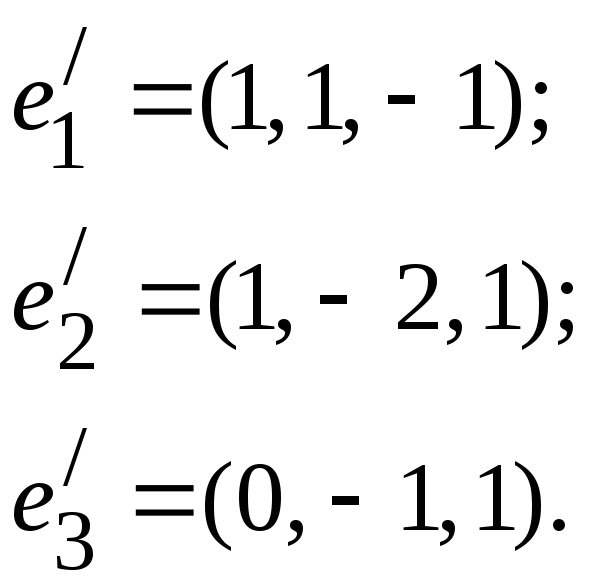
Решение.
Составим матрицу перехода от базиса
![]() к базису
к базису![]() :
:

Найдём обратную
матрицу для
![]() :
:
 .
.
Тогда

