
- •Часть 2. Математическая статистика
- •Тема 1: выборочный метод
- •Задачи для самостоятельного решения:
- •Тема 2: статистические оценки параметров
- •Задачи для самостоятельного решения:
- •Тема 3: статистическая проверка гипотез
- •Задачи для самостоятельного решения:
- •Тема 4: корреляционно-регрессионный анализ
- •Лабораторный практикум по математической статистике
- •Рекомендации к выполнению задачи №1:
- •Проверка гипотезы о равномерном распределении.
Часть 2. Математическая статистика
Тема 1: выборочный метод
Термин «выборочные исследования» применяют, когда невозможно или экономически нецелесообразно изучить все единицы представляющей интерес совокупности. Приходится знакомиться с частью совокупности – с выборкой, а затем с помощью статистических методов и моделей переносить выводы с выборки на всю совокупность.
Пусть
требуется изучить совокупность однородных
объектов относительно некоторого
количественного или качественного
признака, характеризующего эти объекты.
Обозначим количество всех подлежащих
обследованию объектов N
( ).
Допустим, что каждому объектуi
для изучаемого признака X
соответствует
наблюдаемое значение
).
Допустим, что каждому объектуi
для изучаемого признака X
соответствует
наблюдаемое значение
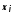 .
Совокупность всех возможных значений
подлежащих обследованию объектов
называетсягенеральной
совокупностью,
а N
– объёмом
генеральной совокупности.
Генеральная совокупность может быть
конечной или бесконечной. Совокупность
случайно отобранных (реально наблюдаемых)
объектов называется выборочной
совокупностью
или просто выборкой,
а её объём обозначается n.
Выборка
должна обладать следующими свойствами:
.
Совокупность всех возможных значений
подлежащих обследованию объектов
называетсягенеральной
совокупностью,
а N
– объёмом
генеральной совокупности.
Генеральная совокупность может быть
конечной или бесконечной. Совокупность
случайно отобранных (реально наблюдаемых)
объектов называется выборочной
совокупностью
или просто выборкой,
а её объём обозначается n.
Выборка
должна обладать следующими свойствами:
каждый элемент
 выбран случайно;
выбран случайно;все
 имеют одинаковую вероятность попасть
в выборку;
имеют одинаковую вероятность попасть
в выборку;n должно быть настолько велико, насколько это позволяет решать задачу с требуемым качеством (выборка должна быть репрезентативной, представительной).
Принято считать, что при n>60 выборка большая, или репрезентативная, а при n<60 – малая. Такое деление выборки на
большую и малую условно. Разные авторы используют разное пограничное n, делящее выборки на большие и малые, которое зависит от решаемой задачи. В зависимости от способа отбора объектов выборки подразделяют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике применяются различные способы отбора, которые принципиально можно подразделить на два вида:
отбор, не требующий расчленения генеральной совокупности на части: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор;
отбор, при котором генеральная совокупность разбивается на части: а) типический отбор; б) механический отбор; в) серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности (лотерея, с помощью таблицы случайных чисел). Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части. Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Часто применяется ком-бинированный отбор, при котором сочетаются указанные способы.
Расположение
выборочных наблюдённых значений
изучаемого признака X
в
порядке неубывания называется
ранжированием.
Значение X,
соответствующее
отдельной группе сгруппированного ряда
наблюдаемых данных, называется вариантой,
а изменение этого значения – варьированием.
Численность отдельной группы
сгруппированного ряда наблюдаемых
данных называется частотой
и обозначается
 ,
отношение
,
отношение называетсяотносительной
частотой и
обозначается
называетсяотносительной
частотой и
обозначается
 .
.
Дискретным
вариационным рядом распределения
называется ранжированная совокупность
вариант
 с соот-ветствующими им частотами или
относительными частотами.
с соот-ветствующими им частотами или
относительными частотами.
Если наблюдаемый случайный признак представляет собой реализацию непрерывной случайной величины или дискретной случайной величины с большим количеством возможных значений, то для построения вариационного ряда используют интервальный ряд распределения. В этом случае весь возможный интервал варьирования разбивают на конечное число частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.
Интервальным вариационным рядом называется упорядоченная последовательность интервалов варьирования случайного признака с соответствующими частотами или относительными частотами попаданий в каждый из них.
Пример 14.1 В супермаркете фиксировали, сколько покупателей обслуживали в кассе за один час. Наблюдения в течение 30 часов
дали следующие результаты:
70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100.
Обработайте результаты наблюдений и постройте вариационный ряд.
Решение: Число покупателей, обслуживаемых в кассе за час, представляет собой реализацию дискретной случайной величины, обозначим её X. Полученные данные являются выборкой из 30 наблюдений. Составим ранжированный ряд распределения:
60, 60, 60, 65, 65, 65, 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75, 100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120.
Получено 6 групп, т.е 6 различных значений случайной величины. Для каждой группы подсчитаем частоту значений варианты и соответствующую относительную частоту.:
|
|
60 |
65 |
70 |
75 |
100 |
120 |
|
|
3 |
3 |
7 |
5 |
8 |
4 |
|
|
3/30 |
3/30 |
7/30 |
5/30 |
8/30 |
4/30 |
Полученная таблица и есть вариационный ряд.
■
Выборочной
функцией распределения или
эмпирической
называется
функция
 ,
задающая для каждого значенияx
относительную частоту события X≤x.
,
задающая для каждого значенияx
относительную частоту события X≤x.
Свойство
статистической устойчивости частоты,
обоснованное теоремой Бернулли,
оправдывает целесообразность использования
функции
 при большихn
в качестве приближённого значения
неизвестной теоретической функции
распределения
при большихn
в качестве приближённого значения
неизвестной теоретической функции
распределения
 .
.
Функции
 и
и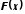 обладают одинаковыми свойствами.
обладают одинаковыми свойствами.
Наблюдаемые данные, представленные в виде вариационного
ряда,
можно изобразить графически, используя
либо график функции
 ,
либо полигон или гистограмму относительных
частот.
,
либо полигон или гистограмму относительных
частот.
Полигоном
относительных частот называют
ломанную, отрезки которой соединяют
точки
 ,
, ,
…,
,
…, .
.
Гистограммой
относительных частот называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат частичные интервалы длины
 ,
а высоты равны отношению
,
а высоты равны отношению .
Площадь гистограммы относительных
частот равна сумме всех относительных
частот, т.е. единице.
.
Площадь гистограммы относительных
частот равна сумме всех относительных
частот, т.е. единице.



