Лекция 4.

Глава 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

$1. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

Если задано некоторое вероятностное пространство (, , Р), то под случайной величиной будем понимать числовую функцию X, заданную на пространстве .

Cлучайные величины будем обозначать большими латинскими буквами, а значения, которые они принимают – соответствующими малыми.

Различают дискретные, непрерывные случайные величины и случайные величины с сингулярным распределением.

Дискретной называется случайная величина, принимающая конечное или счетное число различных значений.

Пример 1. Колесо рулетки разделено на 5 секторов, площади которых относятся как 5:4:3:2:1. Величина выигрыша пропорциональна номеру сектора, наименьший выигрыш –100 рублей.

Будем считать выигрыш случайной величиной Х. Это дискретная случайная величина. Она принимает значения: x₁ = 100,  x₂ = 200, …, x₅ = 500. 

Ecли мы укажем, c какими вероятностями дискретная случайная величина принимает свои значения, то мы зададим распределение случайной величины.

Распределение дискретной случайной величины можно задать в виде таблицы.

В

X	x1	x2	x3	...	xn	...
P	p1	p2	p3	...	pn	...

верхней строчке таблицы указываются значения случайной величины, а в нижней - вероятности этих значений. Вероятность значения случайной величины – это вероятность множества тех элементарных исходов, на которых случайная величина принимает это значение: P(Х = х_n) = Р{: Х() = х_n}.

П

X	100	200	300	400	500
P	1/3	4/15	1/5	2/15	1/15

ример 2. Случайная величина Х из примера 1 принимает свои значения со следующими вероятностями: р₁ = 5/15, р₂=4/15,…, р₅=1/15.



$2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Функцией распределения случайной величины Х называется функция F(x), определяемая на всей действительной прямой как .

Замечание. Поскольку вероятность определена только на множествах из алгебры , не любую числовую функцию Х(),   , можно считать случайной величиной, а только ту, для которой множества {: X()  x}принадлежат алгебре при любом действительном x. Такие функции называются измеримыми.

П

ример 3. Построим график функции распределения случайной величины из примера 1.

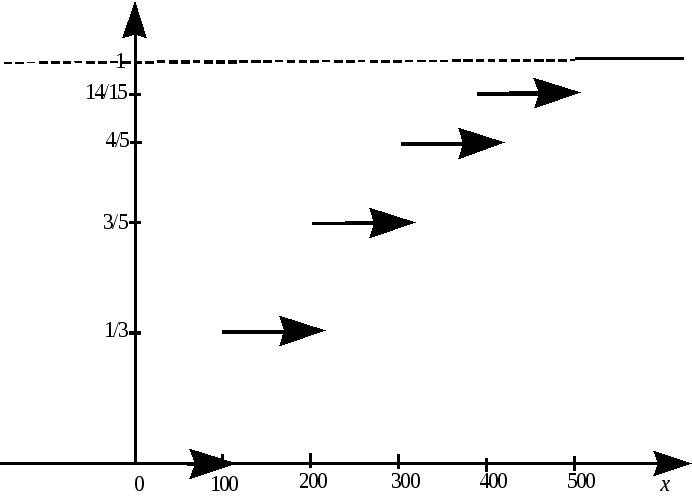
Перечислим свойства функции распределения случайной величины.

Утверждение 1. F(x) не убывает.

Доказательство. Пусть х₁ <  х₂. F(x₂) – F(x₁) = Р(X  x₂) – Р(X  x₁) = = Р{: x₁< X()  x₂)  0. Cледовательно, F(x₁)  F(x₂). 

Утверждение 2. Функция F(x) непрерывна справа, т.е. .

Доказательство. Предположим, F(x) не является непрерывной справа в некоторой точке а: для F(а + ) - F(a) > 0, т.е. P{: а < Х()  a +  } > 0. Значит, с ненулевой вероятностью случайная величины Х принимает значения, которые превосходят а, но не превосходят а +  сразу для всех . Но это невозможно, т.к. любое значение х_{0 ,}большее a, будет превосходить и a +  при некоторых .

Утверждение 3. Будем считать это утверждение аксиомой. 

Замечание. Иногда рассматривают распределения, у которых Такие распределения называются несобственными. Их изучение выходит за рамки нашего курса.

$3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Основной характеристикой случайной величины является математическое ожидание.

Пусть случайная величина Х принимает значения х_k, k= 1,2,… с вероятностями р_k. Математическое ожидание (или среднее значение) дискретной случайной величины обозначается МХ и равняется сумме числового ряда , если ряд сходится абсолютно.

Пример 4. Cредний выигрыш в примере 1 составляет:

MX= 100*(1/3)+200*(4/15)+300*(1/5)+400*(2/15)+500*(1/15)=233,(3). 

Cвойства математических ожиданий:

1. для любой постоянной величины C: MC=C;

2. для любой постоянной a: M(aX)=a*MX;

3. для любых случайных величин X и Y, имеющих математические ожидания MX и MY: M(X+Y)=MX+MY;

4. если случайные величины X() и Y() таковы, что X()  Y() для всех , то МX  MY;

5)

Все свойства математических ожиданий вытекают из свойств абсолютно-сходящихся числовых рядов.

Еще одна характеристика случайных величин – дисперсия. Дисперсия случайной величины X обозначается DX и равняется М(X–MX)².

Дисперсия - это средний квадрат отклонения значений случайной величины от ее математического ожидания.

Из определения дисперсии сразу следуют ее свойства:

1. для любой постоянной величины C: DC=0;

2. для любой постоянной a: D(aX)=а²*D(X).

Утверждение 4. Пусть Х – случайная величина, MX – ее математическое ожидание, а MX ² – математическое ожидание случайной величины X ². Тогда

Доказательство. 

Наряду с дисперсией рассматривают среднее квадратическое отклонение

Пример 5. Дисперсия выигрыша в рулетку DX= MX ²-(MX)².

MX ²= 100²*1/3+200²*4/15+300²*1/5+400²*2/15+500²*1/15=70000; DX = 15555,(5).



$4. МОМЕНТЫ.

Моментом порядка k (k=1,2,3...) случайной величины Х называется математическое ожидание случайной величины X^k .

Пример 6. Моментом первого порядка является математическое ожидание случайной величины. 

Центральным моментом порядка k (k=1,2,3...) называется величина

Пример 7. Центральным моментом второго порядка является дисперсия. 

Утверждение 5. Если распределение случайной величины симметрично относительно ее математического ожидания, то все центральные моменты нечетного порядка, если они существуют, равны 0.

Доказательство. Центральный момент нечетного порядка l представляет собой ряд Поскольку распределение симметрично относительно математического ожидания, то каждому положительному члену ряда соответствует отрицательный, равный ему по модулю. В силу абсолютной сходимости сумма ряда равна 0. 

Для характеристики асимметрии распределения выбрали третий центральный момент. Коэффициентом асимметрии называется величина

Пример 8. Посчитаем коэффициент ассиметрии случайной величины из Х примера 1.



3