Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 22,23

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 22

Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов.

Определение.

Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н₀ отклоняется, когда Н₀ – верна.

Вероятность .

Определение.

Ошибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н₀, но в действительности верна альтернативная гипотеза Н₁.

Вероятность ошибки второго рода при условии, что гипотеза Н₁ – простая, .

Проверка статистических гипотез и доверительных интервалов.

Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал.

Гипотеза Н₀ – принимается, если значение накрывается доверительным интервалом, иначе отклоняется.

§ 9. Проверка гипотезы о распределении совокупности по закону Пуассона с помощью критерия ²

Задача.

ОТК проверил n = 200 партий одинаковых изделий и получил следующее эмпирическое распределение.

xi	0	1	2	3	4
ni	116	56	22	4	2

x_i – количество нестандартных изделий в одной партии.

n_i – частота, которая указывает на количество партий, содержащих x_i – нестандартных деталей.

Требуется на уровне значимости  = 0,05. Проверить гипотезу о том, что число нестандартных изделий – Х, распределено по закону Пуассона.

1. Найдем .

2. В качестве оценки .

.

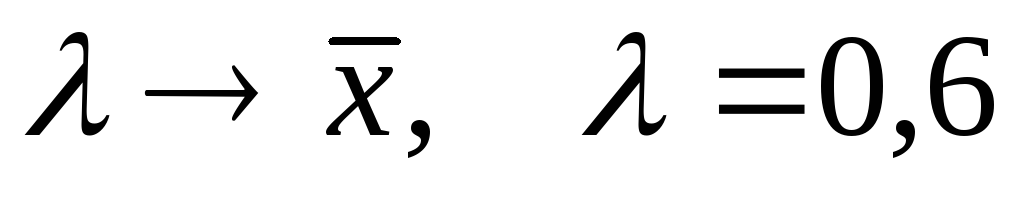3. i = 0, 1, 2, 3, 4

p₀ = 0,5488; p₃ =0,0198

p₁ = 0,3293; p₄ = 0,0030

p₂ =0,0988;

4. np_i – ?

np₀ =109,76

np₁ =65,86

np₂ =19,76

np₃ =3,76

np₄ =0,60

5. 4 + 2 = 6

3,96 + 0,60 = 4,56

i	ni	npi
0	116	109,76	0,3548
1	56	65,86	1,4762
2	22	19,76	0,2539
3	6	4,56	0,4547

Так как в распределении Пуассона оценивается один параметр , то k = 4 – 1 – 1 = .

 нет оснований отвернуть гипотезу о распределении СВ Х по закону Пуассона.

Глава 11

Цепи Маркова

§ 1. Определение цепи Маркова

Непосредственным обобщением схемы независимых испытаний является схема цепей Маркова.

Пусть производится последовательность испытаний, в каждом из которых может осуществляться одно и только одно из k несовместных событий.

верхние индексы обозначают номер испытания.

Определение.

Последовательность испытаний образует простую цепь Маркова, если условная вероятность в испытании, где осуществится событию , зависит только от того, какое событие произошло при S-ом испытании и не изменяется от добавочных сведений о том, какие события происходили в более ранних испытаниях.

Замечание.

Часто при изложении теории цепей Маркова придерживаются иной терминологии и говорят о некоторой физической системе S, которая в каждый момент времени может находиться в одном из состояний и меняет свое состояние только в моменты

Для цепей Маркова вероятность перейти в какое-либо состояние , в момент времени t_S зависит только от самого и того, в каком состоянии система находилась в момент времени и не изменяется оттого, что становятся известными ее состояния в более ранние моменты времени.

Пример 1.

В модели Бора атома водорода, электрон может находиться на одной из допустимых орбит.

Обозначим, через – электрон находится на i орбите и предположим, что изменение состояние атома может наступать только в моменты (в действительности эти моменты представляют собой СВ), то тогда вероятности перехода с i орбиты на j орбиту в момент времени t_S зависит только от i и j и не зависит от того на каких орбитах находился электрон в «прошлом».

Разность (i–j) зависит от количества энергии, на которую изменился заряд атома в момент времени t_S.

Это пример цепи Маркова с бесконечным числом состояний.

§ 2. Матрица перехода

Далее будем рассматривать только однородные цепи Маркова, в которых условная вероятность появления события при условии, что в предыдущем S-ом испытании осуществилось не зависит от номера испытания.

Назовем эту вероятность – вероятностью перехода и обозначим .

Полную вероятностную картину возможных изменений, осуществляющихся при переходе от одного испытания к следующему можно задать с помощью матрицы

– матрица перехода

Замечание.

1. Очевидно, что .

2. Из того, что при переходе из состояния система обязательно переходит в одно из состояний , следовательно, в матрице перехода .

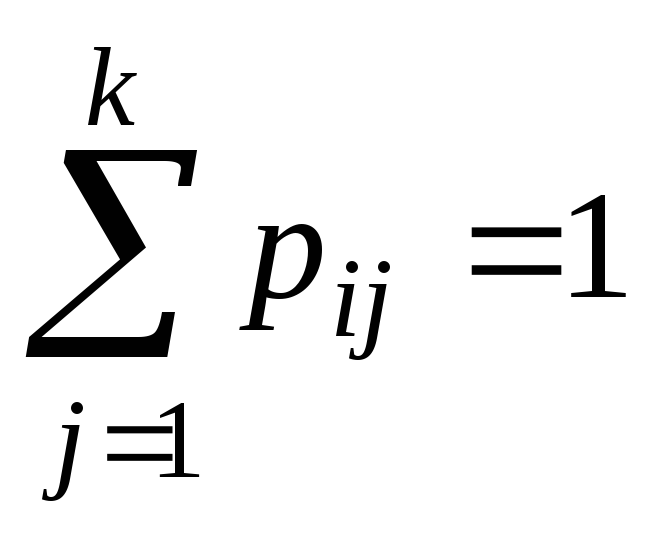Определение.

Любая квадратная матрица, элементы которой удовлетворяют следующим требованиям:

, называется стохастической.

Одной из главных задач в теории цепей Маркова является задача определения вероятности перехода .

Рассмотрим какое-нибудь промежуточное испытание с номером (S+m). В этом испытании осуществится какое-либо одно из возможных событий , тогда вероятность перехода , а вероятность перехода .

По формуле полной вероятности получим

(*)

Обозначим через

Согласно формуле (*) получаем, что .

В частности, когда n = 2, получаем

n = 3

Отметим частный случай формулы (*), когда m = 1

.

Пример 2

Процесс блуждания с отражением.

Пусть частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты времени Частица может находиться в точках с целочисленными координатами . В точках a, b находятся отражающие стенки, каждый толчок перемещает частицу вправо с вероятностью p, а влево с вероятностью q, если только частица не находится у стенки. Если частица находится у стенки, то любой толчок переводит ее на 1 внутрь промежутка между стенками.

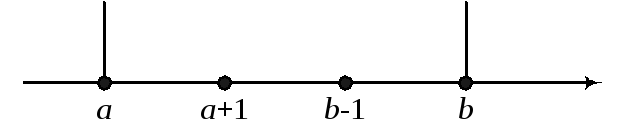
Получается цепь Маркова с конечным числом состояний.

Аналогично можно рассматривать ситуации, когда частица прилипает к одной из стенок, этот процесс блуждания с поглощением.

Лекция № 23

Пример 3.

Вероятности перехода даются матрицей

Чему равно число состояний в системе?

Ответ: 3.

Найти вероятности перехода из состояния в состояние за два шага:

§ 3. Теорема о предельных вероятностях

Теорема

Если при некотором S > 0 все элементы матрицы перехода положительны, то существуют такие постоянные числа , что независимо от индекса имеет место равенство .

Физический смысл этой теоремы.

Вероятность в системе находится в каком-то состоянии практически не зависит от того, в каком состоянии эта система находилась в «далеком прошлом».