Лекция 7

§ 2.5. СВНТ и их законы распределения.

1) , где f_x –плотность распределения вероятности (1)

F_x = P{X<x}

Прямая аналогия с дискретным случаем.

Обратное представление:

2) , если х – точка непрерывности

При таком распределении все скачки сглаживаются.

3) Функция распределения всегда непрерывна у СВНТ.

4) Р{x₁ ≤ Х ≤ x₂}=F_x(x₂)- F_x(x₁)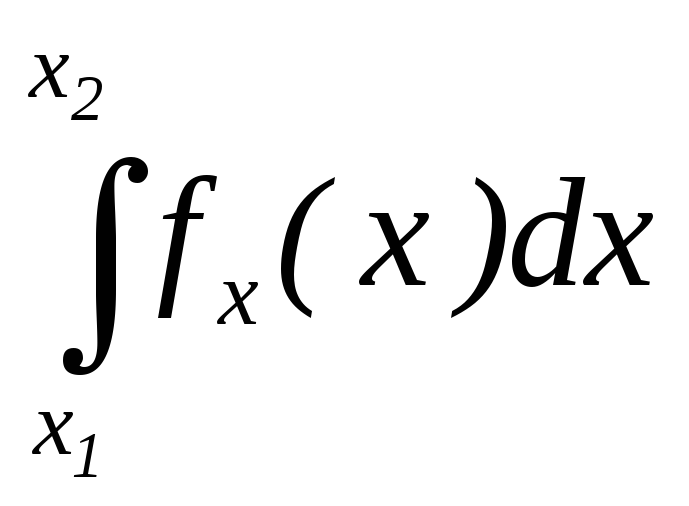= Р{x₁ ≤ Х ≤ x₂} (3)

5) Р{x ≤ Х ≤ x+x}=F_x(x+x)- F_x(x)= F_x(x)=F’_x(x)x+0(x)перейдем к дифференциалам  Р{x ≤ Х ≤ x+dx}= F’_x(x)= f_x(x)dx – вероятность попасть на участок dx.

Определение: f_x(x)dx- называется элементом вероятности.

Числовые характеристики СВНТ.

1. Моменты:

1. начальные: 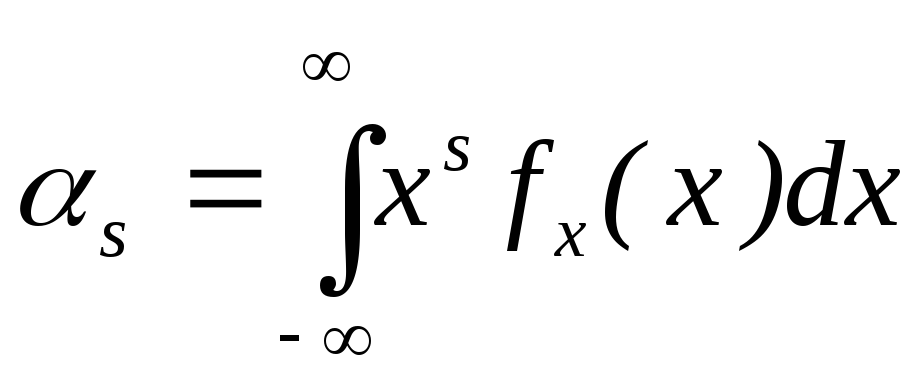(сумма заменяется на интеграл);

б) центральные: .

Частные случаи.

M_x=₁,

₀=1, ₁=0;

Ремарка: Данные характеристики существуют тогда и только тогда, когда данные несобственные интегралы сходятся.

D_x=₁=₂-m_x².

2. Мода: 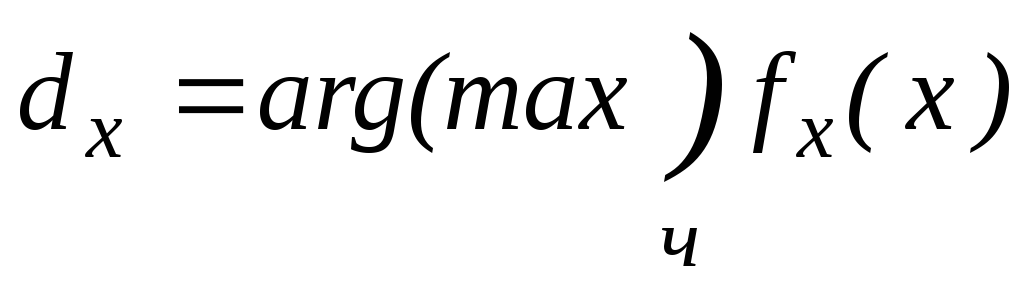- точка на оси х, соответствует максимальной плотности, если она принадлежит Е_х.

3. Медиана: Присуща только непрерывным случайным величинам.

h_x – точка на оси х, для которой вероятность оказаться левее равна вероятности оказаться правее, т.е. Р{Х < h_x}= Р{Х > h_x}

Р{Х < x₀}=0 для любого случая..

Если перейдем к функции распределения, то заметим, что h_x – корень уравнения .

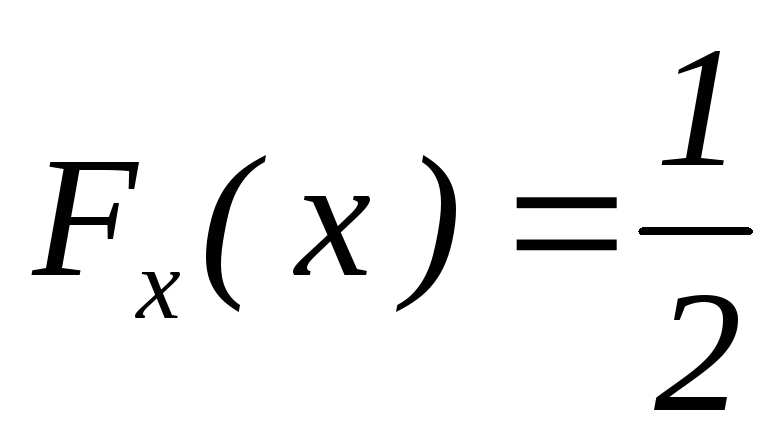Определение: Данные характеристики называются характеристиками положения. Совпадают только в симметричном случае.

§ 2.6. Основные классические распределения непрерывного типа и их характеристики.

1. Равномерное распределение.

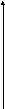f_x=0, при и f_x=,

f_x(х)

a b x

Условия нормировки (обязательное требование к плотности): =1

, ;

Пример: Отчет времени измеряется прибором. Ошибка распределена равномерно между серединами двух соседних линий.

Обозначение: XR(a,b)

2. Показательное (экспериментальное) распределения.

Обозначение: XЕ_х()

f_x=0, при х ≤ 0 или е^-х при х>0;

Пример 1: Модель отказов радиоаппаратуры, приводящая к показательному распределению.

Пусть Х – время безотказной работы радиоаппаратуры. Формализация: пусть известно, что аппаратура проработала х единиц времени без сбоя. Причем, что вероятность отказа радиоаппаратуры за время х, следующее за моментом времени х, пропорциональна х и не зависит от того, сколько времени она проработала без сбоя.

Математика: Р{ Х < x₂+х  Х ≥ x}=х = 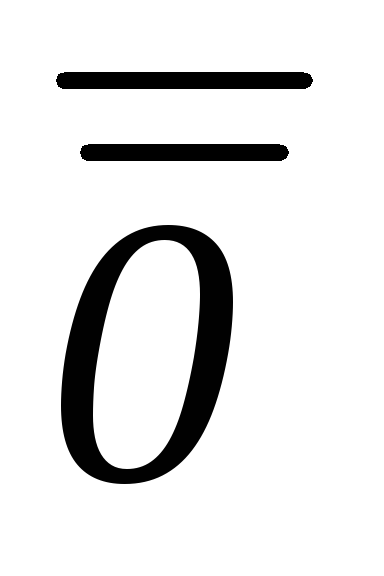(х) (3)

Решение. Ищем закон распределения. Рассмотрим F_х(х)= F_х(х+х)-F_х(х)=

=Р{ х<Х <х+х}=  (используем произведение событий)=(по формуле умножения)= =Р{ Х <х+х Х ≥ х}=(1-F(x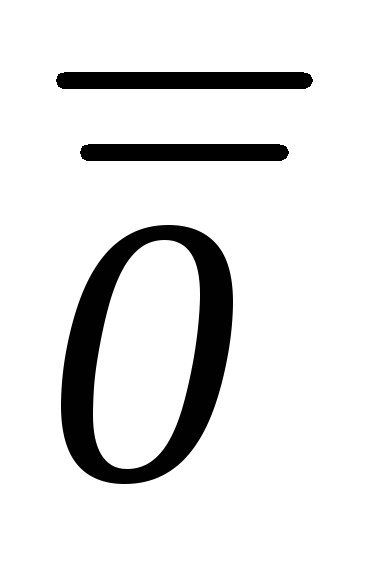)) (х+(х))

, .

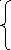
F_x = 0 для х ≤ 0 . начальное условие F_x = 0.

-ln(1- F_x)= х+C

1- F_x=C₁e^-x, C₁= e^c

F_x=1- C₁e^-x

F_x(0)=1- C₁e^-0=1- C₁=0  C₁=1

F_x(x)=1- e^-x

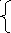0, при х ≤ 0

F_x(x)=

1- e^-x, при х>0.

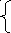
0, при х ≤ 0,

Ответ: f_x = F_x’(x)=

 e^-x, при х>0.

Примеры экспериментов: 1) Время ожидания очереди (массовое обслуживание).

2) Время поиска.

Характеристики экспоненциального распределения:

а) Вычислим

, k=1,2…

, (нормировка).

,

- имеет смысл величины обратной математическому ожиданию.

 D_x= .

б) Вычислим медиану h_x для данного распределения.

F_x(x)= ,

1-=,

=,

x=

3. Нормальное распределение (гаусовское).

Введем обозначения

XN(m,).

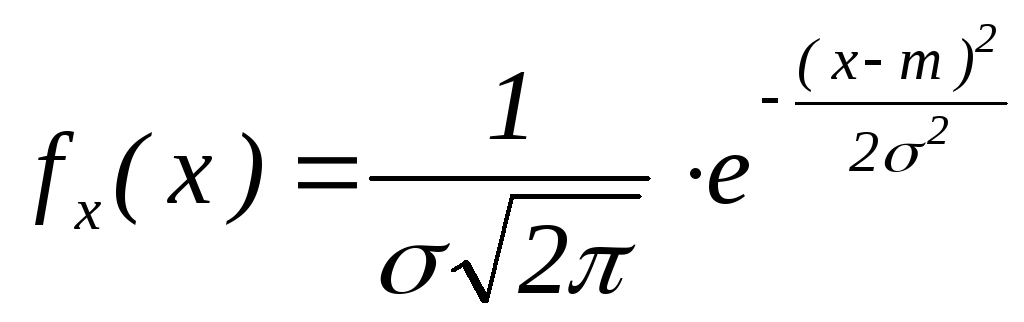,  x  R, m – любое,  >0.

Графически: площадь над гаусовской кривой.

а) Вычислим математическое ожидание.

m_x=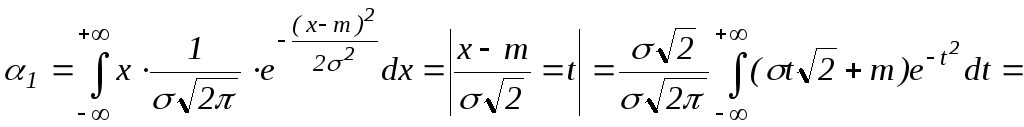

Первый интеграл – интеграл Пуассона и равен , второй интеграл – интеграл от нечетной функции, пределы симметричны  интеграл равен 0.

m_x=m.

б)

,

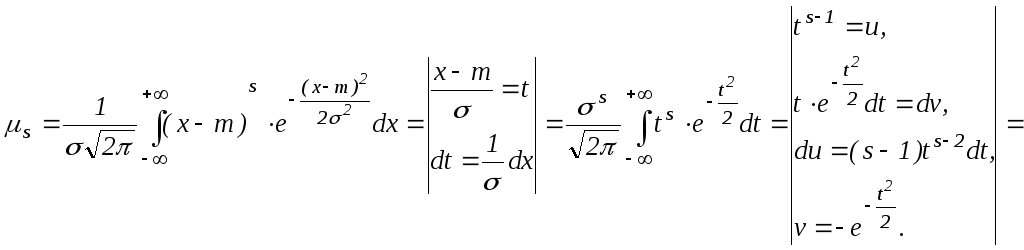
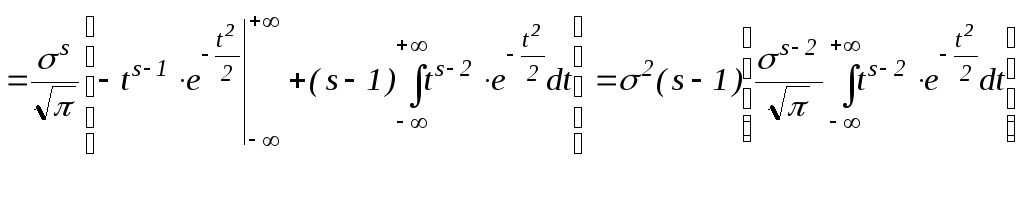(4)

где k=1,2,3….

.

Определение: если XN(0,1), то , называется стандартизированным нормальным распределением. Для него функция распределения имеет вид - интеграл вероятности.

Лекция 9.

Если XN(0,1) (стандартизованное нормальное), то её функция распределения обозначается:

F_x(x)=

Существуют таблицы для x  [0,4], для x>4 с хорошей точностью получается 1.

обладает свойством:

(1)

легко можно получить значения для x<0.

Остальные свойства функции распределения у сохраняется.

Общий случай.

Пусть XN(m,).

Вероятность попадания на интервал:

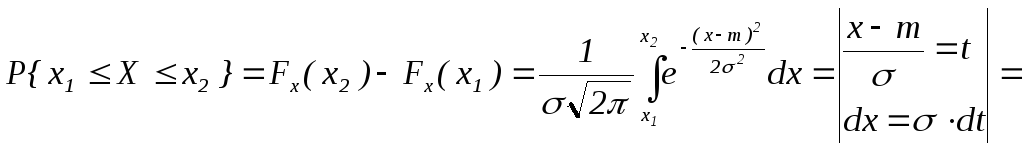
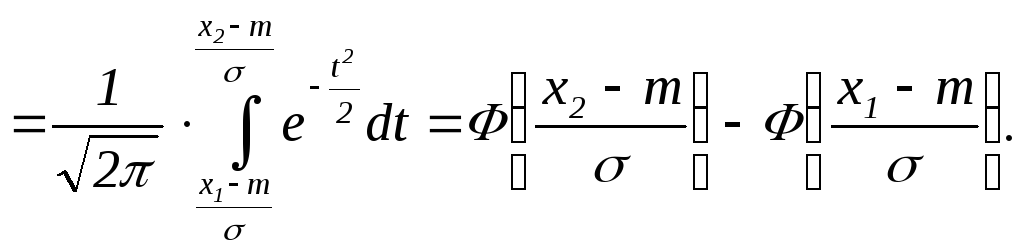
Вероятность попадания на симметричный относительно математического ожидания интервал.

(3)

Пример 1 XN(m,). Вычислить: , k=1,2…

Определение: X-m называется отклонением от математического ожидания.

Решение.

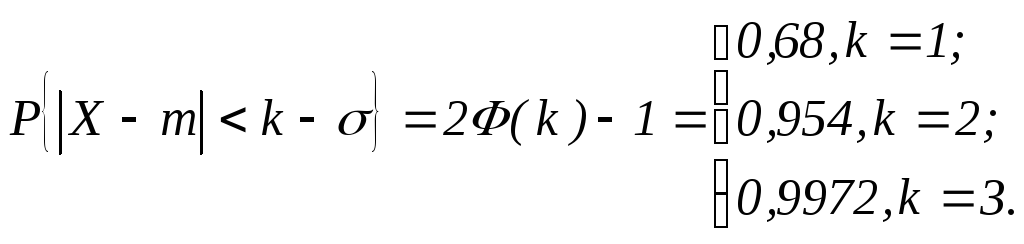
На практике это называется правилом 3-х .

Функция ошибок: , 

Для больших х(>>1) используется асимптотическая формула:

,

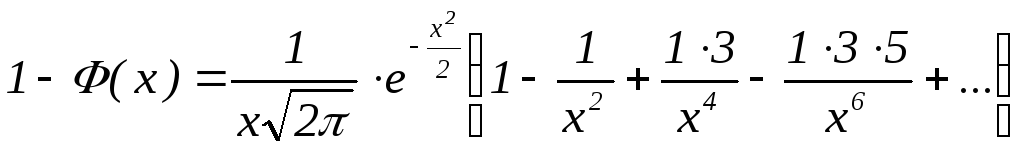при х>4 уже 3 числа ряда дают ошибку ≤ .

Глава 3. Случайные векторы

Очень часто результаты эксперимента описываются несколькими случайными величинами.

§ 3.1. Основные понятия. Свойства функции распределения.

Определение: пусть в данном эксперименте определенны n случайных величин: X₁(w), X₂(w)…X_n(w). Рассматривая их совместно можно получить вектор X={ X₁(w), X₂(w)…X_n(w)}. Для этого вектора определенны все случайные события.

Для каждого такого вектора можно построить многомерную функцию распределения: .

.

Подробнее остановимся на двумерном случайном векторе и опишем свойства функции распределения.

Свойства двумерной функции распределения.

1).

Геометрически:

y

(x,y)

Г(x,y) Вероятность попасть в прямой угол на плоскости.

x где .

2)

3)

Доказательство.

Аналогично для

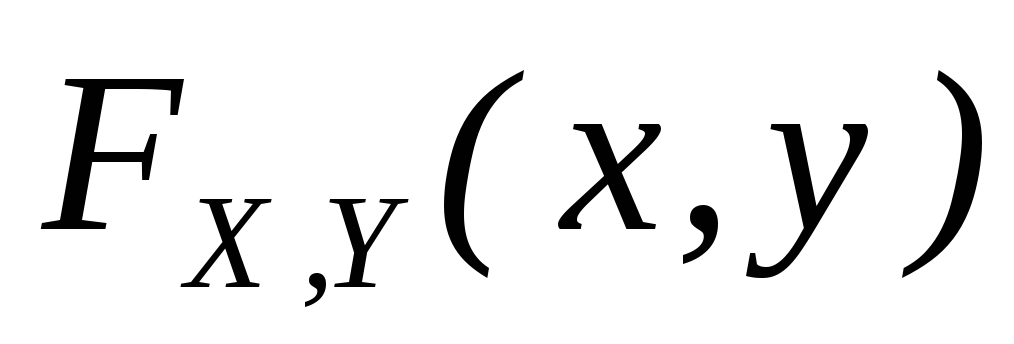4. - неубывающая функция по каждой переменной

Доказательство.

Пусть x₂>x₁  {X<x₁,y}<{X<x₂,y}  по свойству вероятности получаем результат.

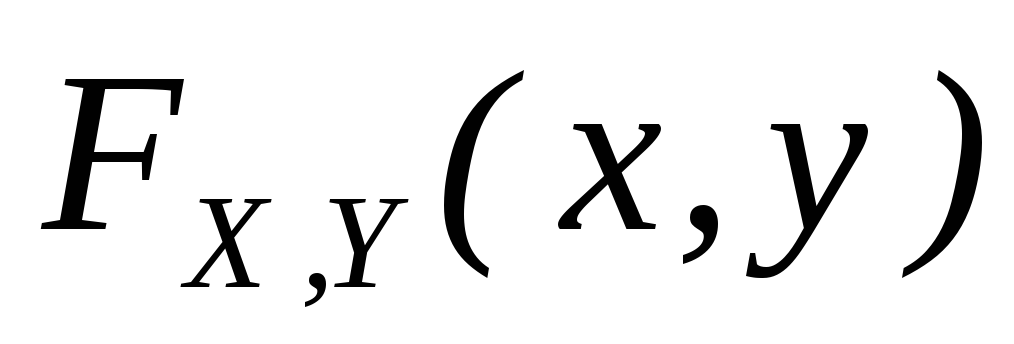5. - непрерывна слева по каждому аргументу.

(смотри одномерный случай).

6. Вероятность попадания в прямоугольник:

П={(x,y) x₁≤ x<x₂, y₁≤ y<y₂}

у

у₂

П

у₁

х

х₁ х₂

P{(Х,Y)  П}= Р{х₁ ≤ Х < х₂, y₁ ≤ Y< y₂}= F_X,Y(x₂, y₂) + F_X,Y(x₁, y₁) - F_X,Y(x₁, y₂) -

- F_X,Y(x₂, y₁) (4)

Доказательство.

Рассмотрим событие A_ij={X<x_i,Y<y_j}.

Событие C=A₁₂+A₂₁.

Учтем, что A₂₂=П+С, причем ПС=  по аксиоме сложения:

Р(А₂₂)=Р(П)+Р(С) Р(П)=Р(А₂₂)-Р(С)=Р(А₂₂)-Р(С)=Р(А₂₂)+Р(А₁₁)-Р(А₁₂)-Р(А₂₁).

§ 3.2. Случайные векторы дискретного типа (СВДТ) и их законы распределения.

Определение: случайный вектор (СВ) называется СВДТ, если множество его возможных значений E_X,Y – конечно или счетно.

Определение: закон распределения СВДТ – это таблица вида:

xi	y1	y2	……..	ym	pi=Px= xi
x1	p11	p12	…….	p1m	p1
x2	p21	p22	…….	p2m	p2
…….	………..	……….	…….	…….	…….
xn	pn1	pn2	…….	pmn	pn
pj=PY= yi	p1	p2	…….	pm	1

Необходима нормировка:

Можно использовать свободные строку и столбец (6-ые).

Возникают следующие задачи:

Задача 1. По известному закону распределения СВ (X,Y) (известна основная таблица) восстановить законы распределения отдельных компонент.

Решение.

Рассмотрим в качестве гипотез.

H_j={Y=y_j}  P{X=x_i}=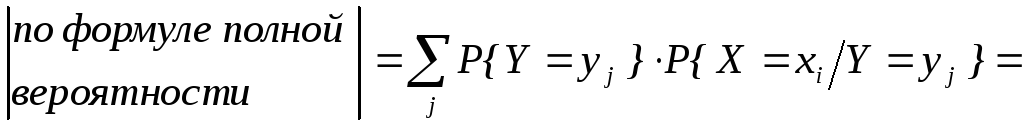



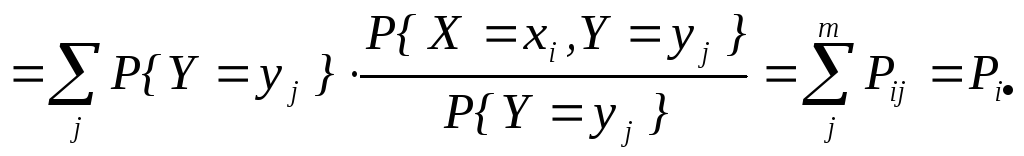
 в последнем столбце записываются .

Задача 2. Можно ли и как это сделать?

По закону распределения отдельных компонент восстановить закон распределения всего вектора (обратная задаче 1).

Решение.

/*Задача не решается однозначно.*/

Пусть X и Y распределены одинаково согласно таблицам.

X	-1	1
p	½	½
Y	-1	1
p	½	½

Построим следующие две таблицы:

xi\ yi	-1	1	pi
-1	½	0	½
1	0	½	½
pj	½	½	1

xi\ yi	-1	1	pi
-1	¼	¼	½
1	¼	¼	½
Pj	½	2	1

Два абсолютно разных распределения  Восстановить однозначно нельзя.

Задача 3. По закону распределения СВ (по известной таблице) построить функцию распределения F_X,Y(x,y)

Решение.

F_X,Y(x,y)=P(X,Y) Г(х,у)=

Задача 4. (обратная к задаче 3). По заданной функции распределения восстановить таблицу распределения.

Решение.

1. Выявим точки скачка функции распределения  восстановим спектр.

2. Определим вероятность каждого дискрета.

Пример:

y

x x x

x x x

Берем малый прямоугольник (см. рисунок) и используем формулу попадания в прямоугольник.

§ 3.3. Независимость случайных событий.

Определение: Случайные величины X, Y называются независимыми, если выполняются условия:

F_X,Y(x,y)= F_X(x)F_Y(y) (5)

Теорема 9.1. Для независимости X и Y необходимо и достаточно, чтобы P_{i j} = P_i= P_{ j}

 i, j из основной таблицы распределения

Доказательство: Пусть P_{i j} = P_i= P_{ j}  F_X,Y(x,y)=(согласно задаче 3) = =

== F_X(x)= F_Y(y)

{X<x_i}, {Y<y_j}. Достаточность доказана.