Тема 03

РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ. СЛУЧАЙНЫЕ ПРОЦЕССЫ.

Тема 3. Случайные величины, дискретные и непрерывные. Функции распределения.

•Определение случайной величины и функции распределения вероятностей.

•Дискретные случайные величины. Непрерывные случайные величины.

•Биномиальное распределение. Распределение Пуассона.

•Равномерное, нормальное, хи-квадратичное, экспоненциальное и др. распределения.

Определение случайной величины и функции распределения вероятностей.

Случайной называют величину, которая в результате испытания примет одно и только возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0,1,2,…,100.

Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин, которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (a, b).

Будем далее обозначать случайные величины прописными буквами X,Y,Z, а их возможные значения – соответствующими строчными буквами x,y,z. Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: x1, x2 , x3 .

Таким образом, целесообразно различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Рассмотрим случайную величину Х, возможные значения которой сплошь заполняют интервал (a, b). Можно ли составить перечень всех возможных значений Х? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин. С этой целью и вводят функции распределения вероятностей случайной величины.

Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. вероятность события X < x , обозначим через F(x) . Разумеется,

если х изменяется, то, вообще говоря, изменяется и F(x) , т.е. F(x) - функция от х.

Функцией распределения называют функцию F(x) , определяющую вероятность того, что

случайная величина Х в результате испытания примет значение, меньшее х, т.е.

F(x) = P(X < x) .

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что

случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Свойства функции распределения.

1) Значения функции распределения принадлежат отрезку [0;1]:

0 ≤ F(x) ≤1.

2) F(x) - неубывающая функция, т.е.

F(x2 ) ≥ F (x1) , если х2 > х1 .

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале

Р(а ≤ Х ≤ b) = F(b) − F(a) .

Пример 3. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0;2).

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

3)Если возможные значения случайной величины принадлежат интервалу (a, b), то

при х ≤ а F(x) = 0 , при x ≥ b F(x) =1.

Следствие 3. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

График функции распределения.

Описанные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

1)График расположен в полосе, ограниченной прямыми y=0 и y=1.

2)При возрастании х в интервале (a, b), в котором заключены все возможные значения случайной величины, график «поднимается вверх».

3) При х ≤ а ординаты графика равны нулю; при x ≥ b ординаты графика равны единице.

График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере.

Найти функцию распределения и начертить ее график.

Дискретные случайные величины. Непрерывные случайные величины.

На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так, случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

Таблично

Приняв во внимание, что в одном испытании случайная величина принимает одно и

бесконечно (счетно), то ряд р1 + р2 +...сходится и его сумма равна единице.

Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (хi ; рi ), а затем

соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Функция распределения непрерывной случайной величины полностью характеризует случайную величину, однако имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Плотностью распределения вероятностей случайной величины Х называют функцию f (x) - первую производную от функции распределения F(x) : f (x) = F′(x) .

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает, как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a;b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

b

Р(а < X < b) = ∫ f (x)dx .

a

Свойства плотности распределения.

1) Плотность распределения – неотрицательная функция: f (x) ≥ 0 .

2) Несобственный интеграл от плотности распределения в пределах от −∞ до + ∞ равен

1:

+∞∫ f (x)dx =1.

−∞

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения (графиком функции распределения), равна 1.

В частности, если все возможные значения случайной величины принадлежат интервалу

(a;b), то

∫b f (x)dx =1.

a

Основные законы распределения: биномиальный закон распределения.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (тогда вероятность непоявления q=1-p). Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины Х. Для ее решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: х1 = 0 , х2 =1, х3 = 2 , …, хn+1 = n . Остается

найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли (1654-1705, его работы способствовали развитии. Применений только что возникших дифференциального и интегрального исчислений; название «интеграл» впервые появилось в трудах Якоба Бернулли) (по ней находится вероятность появления k раз события А в n испытаниях):

Формула (*) и является аналитическим выражением искомого закона распределения.

Биномиальным называется распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона:

(p + q)n = Cnn pn +Cnn−1 pn−1q +... +Cnk pk qn−k +... +Cn0qn .

Таким образом, первый член разложения pn определяет вероятность наступления рассматриваемого события n раз в n испытаниях; второй член npn−1q определяет вероятность наступления события n-1 раз;…; последний член qn определяет вероятность того, что событие не появится ни разу.

Пример 7. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биномиальный закон распределения дискретной случайной величины Х – числа нестандартных деталей и построить многоугольник полученного распределения.

Биномиальный закон действует и в биологических совокупностях: по нему распределяются альтернативные, дискретно варьирующие признаки. Для примера возьмем соотношение между численностью мужских и женских особей в популяциях животных, которое равно примерно 1:1 или приближается к этому отношению. Какова вероятность, что из 10 новорожденных три окажутся мужского пола? По условию задачи

вероятности всех возможных случаев осуществления ожидаемого события, т.е. вероятность появления мужского пола в каждом из 10 случаев появления на свет потомства, то результаты распределяются следующим образом:

Видно, что с увеличением числа m вероятность P10 (m) сначала быстро возрастает, достигая максимума при P10 (5) = 1024252 , а затем в такой же последовательности убывает. Эти данные

показывают, что слишком мала вероятность ожидать, чтобы все десять новорожденных оказались мужского пола. Наиболее вероятный исход – равное отношение полов среди новорожденных.

Формула Бернулли дает абсолютно точный ответ для вероятности Pn (k) . Но, при больших

n, абсолютная точность не упрощает, а усложняет получение ответа в большинстве приложений. Но раз точные ответы для вероятности Pn (k) вычислить сложно, то, может

быть, существуют те или иные способы приближенных вычислений? Да, такие приближения действительно возможны! Более того, удивительным образом оказалось, что в огромном числе различных ситуаций все эти приближения могут быть произведены с помощью одной-единственной функции y =ϕ(x) , с которой мы познакомимся чуть

позже.

Закон распределения Пуассона.

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа (1749-1827, крупнейший французский математик, механик и астроном. Отношение Пьера Симона Лапласа к науке ярко передает следующий эпизод. Когда Наполеон, бывший большим почитателем таланта Лапласа, обратился к ученому с вопросом, почему в опубликованной им «Небесной механике» нет даже упоминания о боге, Лаплас ответил фразой, ставшей впоследствии знаменитой: «Эта гипотеза мне не понадобилась»). Однако эта формула непригодна, если вероятность события мала ( р ≤ 0,1). В этих случаях (n велико, р мало) прибегают к асимптотической

формуле Пуассона (1781-1840, выдающийся французский математик и физик).

Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно np = λ . Это означает, что среднее число появлений события в различных сериях

испытания, т.е. при различных n, остается неизменным.

Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:

Приняв во внимание, что n имеет очень большое значение, вместо Pn (k) найдем lim Pn (k) .

n→∞

При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение np сохраняет постоянное значение, то при n → ∞ вероятность

р → 0 .

вероятностей массовых (n велико) и редких (р мало) событий.

Пример 8. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Имеются специальные таблицы, пользуясь которыми можно найти Pn (k) , зная k и

λ (приложение 3). Обратите внимание на то, что чем больше λ , тем больше m, для которых значения вероятностей не равны нулю, т.е. тем длиннее таблица.

Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства. Оно описывает число событий k, происходящих за одинаковые промежутки времени при условии, что события происходят независимо друг от друга с постоянной средней интенсивностью. Например, число покупателей, посетивших супермаркет в течение часа, число аварий на отрезке дороги, число дефектов на участке водопровода, число посетителей музея в неделю.

Формула Пуассона описывает также очень многие явления, с которыми биологи встречаются в своей работе. Наиболее часто такие редкие случайные события наблюдаются в области микробиологии, радиобиологии, биофизики и других отраслях биологической науки.

Основные законы распределения непрерывных случайных величин: равномерный закон распределения.

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называются также законами распределений.

Равномерное распределение непрерывной случайной величины встречается в тех ситуациях, когда мы имеем дело с различными циферблатами (часы, весы, физические приборы и т.д.). Также равномерное распределение возникает как распределение ошибок при округлении чисел. Распределение вероятностей называется равномерным, если на интервале [a; b], которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение, а вне его равна нулю:

Так как все возможные значения случайной величины принадлежат интервалу [a; b], то должно выполняться соотношение

a

Тогда искомая плотность вероятности равномерного распределения

График плотности равномерного распределения:

Лекции по математике. Тема 3 Страница 8

График функции равномерного распределения:

Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Вероятность попадания случайной величины в заданный интервал:

Пример 9. Непрерывная случайная величина задана функцией распределения

Найти: 1) значение А; 2) вероятность того, что в результате испытания Х примет значение в интервале (0;2); 3) плотность вероятности f (x) .

Показательный закон распределения.

Показательное распределение встречается, когда имеют дело с распределением времени совершенно случайных событий. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

Мы видим, что показательное распределение определяется одним параметром λ . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров.

Найдем функцию распределения показательного закона:

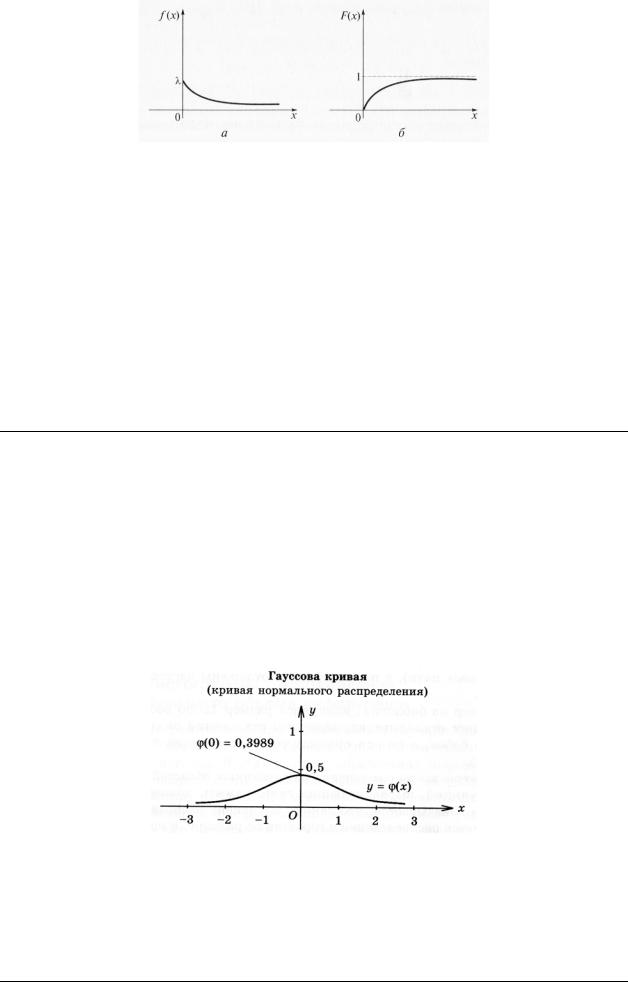
Графики плотности вероятности и функции распределения приведем на рисунке:

Пример 10. Написать плотность и функцию распределения показательного закона, если параметр λ =8.

Найдем вероятность попадания в интервал (а; b) непрерывной случайной величины Х, которая распределена по показательному закону, заданному функцией

распределения F(x) =1 −e−λx (x ≥ 0) . Используем

формулуP(a < X < b) = F(b) − F(a) . Учитывая, что F(a) =1 −e−λa , F(b) =1 −e−λb , получим P(a < X < b) = e−λa −e−λb .

Пример 11. Непрерывная случайная величина Х распределена по показательному

Х попадает в интервал (0,3;1).

Нормальный закон распределения.

Нормальный закон занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Оказывается, что такому же закону распределения подчиняется распределение и горошин по размеру, и новорожденных младенцев по весу, и частиц газа по скоростям движения, и огромное количество других явлений окружающего мира. Подобно тому, как графики всех парабол получаются с помощью преобразований из одной-единственной параболы

y = x2 , так и все эти кривые распределения получаются из одной-единственной кривой.

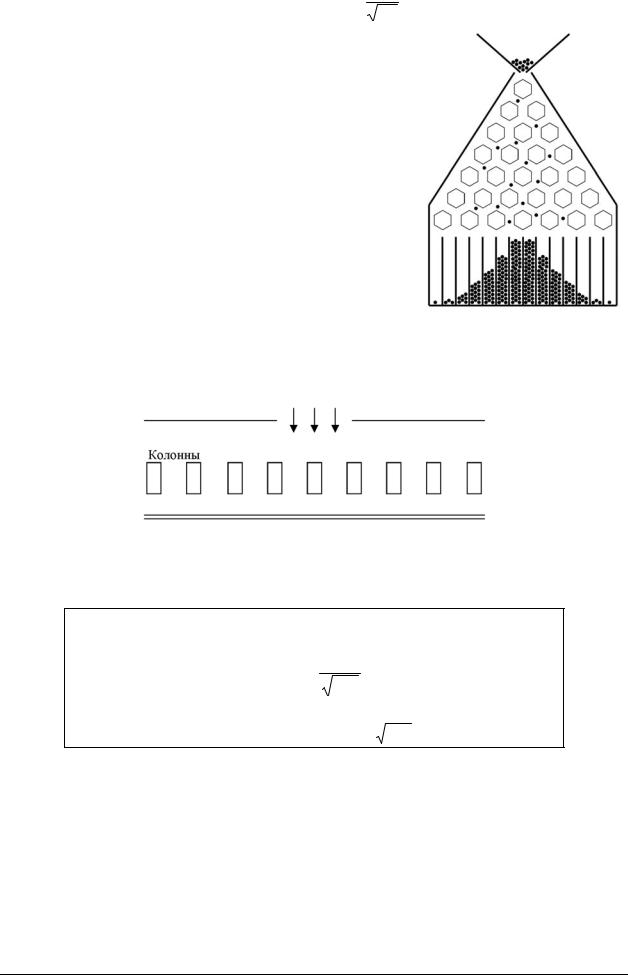
Ее называют кривой нормального распределения или, в честь немецкого математика Карла Гаусса, гауссовой кривой – она изображена на рисунке:

Эта «колоколообразная» кривая симметрична относительно оси ординат и имеет единственный максимум. Площадь части плоскости, ограниченной гауссовой кривой и осью Ох равна единице. Ее ветви очень быстро приближаются к оси абсцисс: если найти площадь «под гауссовой кривой» на отрезке [-3;3], то получится более 0,99, т.е. больше 99% всей площади. Для гауссовой кривой выбрано специальное обозначение y =ϕ(x) .

использования эта формула практически не нужна. Для значений этой функции составлены подробные числовые таблицы (см. Приложение 1).

Для наглядной демонстрации нормального (гауссова) закона распределения иногда используют специальное устройство, названное по имени его изобретателя доской Гамильтона. В нем падающие сверху шарики распределяются между правильными шестиугольниками и в результате попадают на горизонтальную поверхность, образуя картинку, похожую на «подграфик» гауссовой кривой.

Вот еще одна иллюстрация нормального закона распределения. Пассажиры метро бегут по переходу, выходящему на середину станции. Бегут они на поезд, стоящий напротив выхода из перехода. Платформа, у

которой стоит поезд, равномерно разделена колоннами. Ясно, что большинство пассажиров войдет в средние вагоны, а по мере удаления вагонов от центра количество садящихся в них людей будет уменьшаться. Распределение пассажиров по вагонам снова напоминает нормальное, или гауссово, распределение.

Напомним, что выше говорилось о возможности использования функции y =ϕ(x) для приближенных вычислений вероятности Pn (k) в испытаниях, проводимых по схеме Бернулли.

Алгоритм использования функции ϕ(x) в приближенных вычислениях

1)Проверить справедливость неравенства npq >10 ;

2)вычислить х по формуле x = k −npqnp ;

3)по таблице найти значение ϕ(x) ;

4) предыдущий результат разделить на npq .

Пример 12. Вероятность рождения мальчика примем равной 50%. Найти вероятность того, что среди 200 новорожденных будет ровно: а) 110 мальчиков; б) 80 мальчиков.

Рассмотрим внимательнее неравенство npq >10 из первого пункта приведенного

алгоритма. Так как q=1-p, то pq=p(1-p) и наибольшее значение этого квадратичного выражения (относительно p [0;1]) достигается при p=0,5. Само наибольшее значение

равно 0,25. Значит, 0,25n ≥npq>10. Поэтому 0,25n>10, т.е. n>40.