Лекция 18. Теоремы о среднем значении

Лекция 18. Теоремы о среднем значении.

18.1. Теоремы о среднем значении.

Определение 18.1. Функция достигает в точке локального максимума (минимума), если существует окрестность этой точки, на которой выполняется неравенство или для (соответственно или для ). Локальный максимум и локальный минимум называются локальным экстремумом.

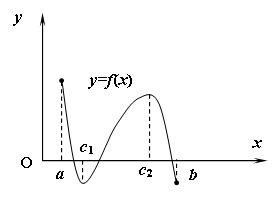
☼ Замечание 18.1. Если функция непрерыв­на на отрезке и достигает на нём максимума (ми­нимума) в точке , то, очевидно, точка c явля­ется в то же время точкой локального максимума (ми­нимума) . Другое дело, если максимум (минимум) на достигается в одной из концевых точек отрезка. Такая точка не является точкой локального максимума (минимума) , т.к. не определена в полной окрестности концевых точек (см. рис. 18.1). ☼

Рис. 18.1.

♦ Теорема 18.1 (Ферма¹). Пусть функция определена на интервале . Если функция имеет производную в точке и достигает в этой точке локального экстремума, то .

Доказательство. Для определённости будем считать, что имеет в точке c локальный максимум. По определению производной .

Так как для , то при , т.е.

. (18.1)

Если же , то , т.е.

. (18.2)

Из (18.1) и (18.2) вытекает, что . ■

♦ Теорема 18.2 (Ролля²). Если функция непрерывна на , дифференцируема на и , то существует, по крайней мере одна, точка такая, что .

Доказательство. 1) Если постоянна на , то для всех производная .

2) Будем считать, что непостоянна на . Т.к. непрерывна на , то существует точка , в которой достигает максимума на , и существует точка , в которой достигает минимума на .

Обе точки , не могут быть концевыми точками, иначе

и была бы постоянной на . Следовательно, одна из точек , принадлежит интервалу . Обозначим её . В ней достигается локальный экстремум. Кроме того, существует, потому что по условию существует для всех точек . Поэтому, по теореме Ферма . ■

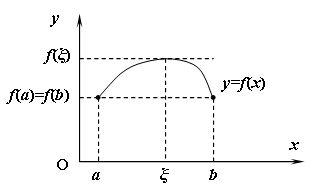
☼ Замечание 18.2. Теорема Ролля сохраня­ет силу также для интервала , лишь бы вы­полнялось соотношение . ☼ ☼ Замечание 18.3. Теорема Ролля имеет простой геометрический смысл. Если выполнены условия теоремы, то на графике функции существует точка , касательная в которой параллельна оси Ox. (см. рис. 18.2). ☼

Рис.18.2.

♦ Теорема 18.3 (Коши¹). Если функции и непрерывны на , дифференци­руемы на и в , то существует точка такая, что .

Доказательство. Заметим, что , т.к. иначе по теореме Ролля нашлась бы точка : , чего не может быть по условию теоремы.

Составим вспомогательную функцию . Функ­ция непрерывна на , дифференцируема на и (проверить!). По теореме Ролля существует точка , в которой . Но . Подставим и получим, что . ■

☼ Замечание 18.4. В формуле Коши необязательно , можно взять . ☼

♦ Теорема 18.4 (Лагранжа²). Пусть функция непрерывна на , имеет производную на . Тогда существует точка для которой .

Доказательство. Введём функцию . Функция удовле­творяет условиям теоремы Ролля: 1) непрерывна на ; 2) дифференцируема на ; 3) , . Следовательно, существует точка : . Но и получаем, что , . ■

☼ Замечание 18.5. Теорему Лагранжа можно доказать как следствие теоремы Коши, взяв .

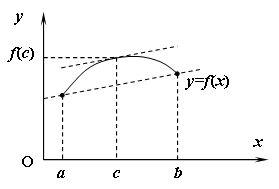
Теорема Лагранжа имеет простой геометрический смысл. Запишем её в виде

. (18.3)

Левая часть равенства (18.3) – это тангенс угла на­клона к оси Ox хорды, стягивающей точки и графика функции , а правая часть – тан­генс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой . Таким обра­зом, если кривая есть график непрерывной на функ­ции, имеющей производную на , то на этой кривой существует точка, соответствующая некоторой абсциссе , такая что касательная в этой точке параллельна хорде, стягивающей концы кривой и .

Рис. 18.3.

Формула (18.3) называется формулой конечных приращений. Промежуточное значение c удобно записывать в виде , где . Формула Лагранжа:

.

Она верна не только для , но и для . ☼

 Пример 18.1. Оценим .

. По теореме Лагранжа

. 

♦ Теорема 18.5. 1) Функция , непрерывная на отрезке и имеющая неотрицательную (положительную) производную на интервале , не убывает (строго возрастает) на отрезке .

Доказательство. Пусть . По теореме Лагранжа существует точка , для которой . Если , то – функция не убывает. Если , то – функция строго возрастает. ■

♦ 2) Функция , непрерывная на отрезке и имеющая неположительную (отрица­тельную) производную на интервале , не возрастает (строго убывает) на отрезке .

Доказательство аналогично пункту 1). ■

 Пример 18.2. Функция имеет непрерывную производную для .

, .

Следовательно, она (функция) строго возрастает и непрерывно дифференцируема на . Поэтому она имеет обратную однозначную непрерывно дифференцируемую функцию , . 

♦ Теорема 18.6. Если функция имеет на интервале производную, равную нулю, то она постоянна на .

Доказательство. По теореме Лагранжа , – фиксированная точка, x – произвольная точка, (или ). Так как , то и для . ■

18.2. Правило Лопиталя.

♦ Теорема 18.7 (1-е правило Лопиталя¹). Пусть функции и определены и дифференцируемы в окрестности точки , за исключением, быть может, самой точки a, и , в . Тогда, если существует , то существует и .

Доказательство. Будем считать, что a – конечное число. Доопределим функции и в точке . Пусть . Тогда эти функции будут непрерывны в точке a. На функции и непрерывны, на дифференцируемы. По теореме Коши существует точка в которой , ,

, (18.4)

при условии, что предел в правой части равенства существует. ■

☼ Замечание 18.6. Может быть так, что существует , но не существует . ☼

 Пример 18.3. , поэтому .

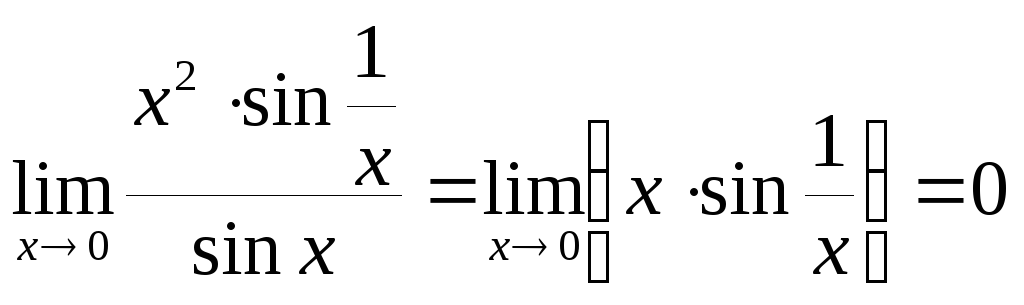Но 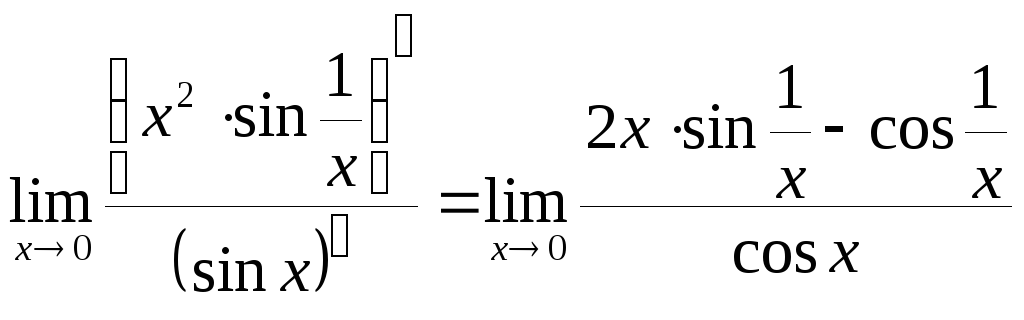не существует. 

☼ Замечание 18.7. Если выражение представляет собой неопределённость вида и функции и удовлетворяют условиям теоремы Лопиталя, то

. ☼

♦ Теорема 18.8 (2-е правило Лопиталя). Пусть функции и определены и дифференцируемы в окрестности точки и , , в этой окрестности. Тогда, если существует , то существует и .

Доказательство аналогично доказательству теоремы 18.7. ■

☼ Замечание 18.8. Если , то замена приведёт к :

. ☼

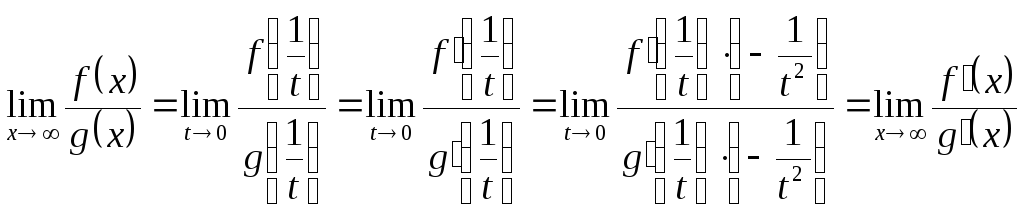 Пример 18.4. 1) , .

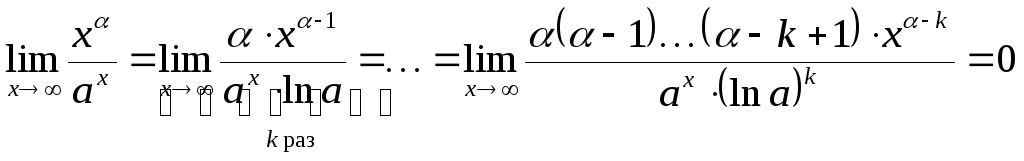
2) для . 

18.3. Раскрытие неопределённостей.

1) Неопределённость вида для выражения вида (, при ) сводится к неопределённости или :

или .

 Пример 18.5. для . 

2) Неопределённости вида , , для выражения вида сводятся к неопреде­лённости :

;

если , то .

 Пример 18.6. . Следовательно,

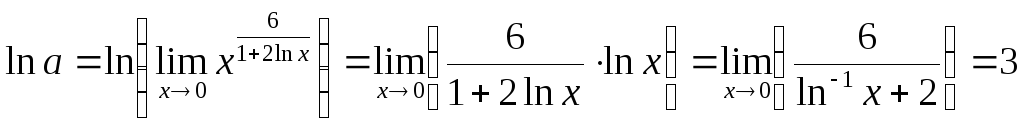, откуда . 

3) Неопределённость вида для выражения вида (, при ) сводится к неопределённости :

.

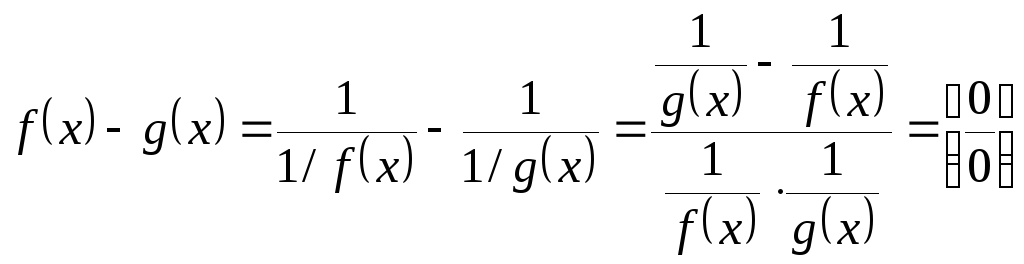 Пример 18.7.

. 

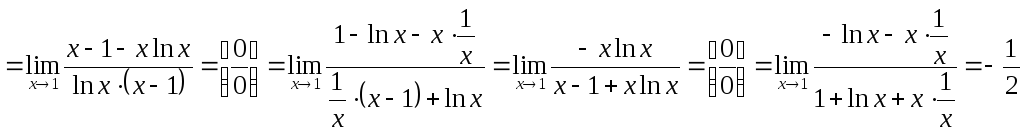1 Ферма Пьер (1601-1665) – французский математик.

2 Ролль Мишель (1652-1719) – французский математик.

1 Коши Огюстен Луи (1789-1857) – французский математик.

2 Лагранж Жозеф Луи (1736-1813) – французский математик и механик.

1 Лопиталь де Гийом Франсуа Антуан (1661-1704) – французский математик. Правило, носящее его имя, было известно швейцарскому математику Иоганну Бернулли (1667-1748).

85