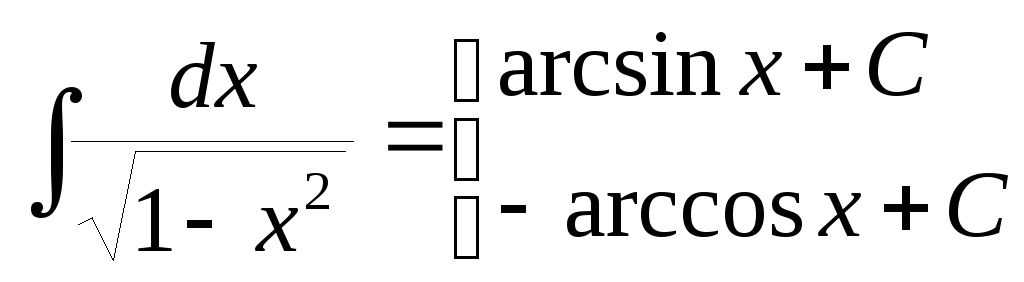Лекция 21. Неопределенный интеграл

Лекция 21. Неопределённый интеграл.

21.1. Понятие неопределённого интеграла.

Пусть известна производная от функции и требуется найти саму функцию . С физической точки зрения это означает, что по известной скорости движения материальной точки необходимо восстановить закон её движения.

Определение 21.1. Функция называется первообразной функцией для функции на интервале , если дифференцируема на и .

Аналогично можно определить первообразную и на отрезке , но в точках a и b надо рассматривать односторонние производные.

 Пример 21.1. 1) – первообразная функция для функции на , так как на этом интервале .

2) – первообразная функция для функции на , так как на этом интервале . 

♦ Теорема 21.1. Если – первообразная для функции на интервале , то – также первообразная, где .

Доказательство. Имеем . ■

♦ Теорема 21.2. Если и – две первообразные для функции на интервале , то на , где .

Доказательство. . Составим функцию и найдём её производную: для . Следовательно, , то есть . ■

Таким образом, из теорем 21.1 и 21.2 вытекает, что если – первообразная для на , то любая другая первообразная для на имеет вид .

Определение 21.2. Произвольная первообразная для функции на интервале называется неопределённым интегралом от функции и обозначается , где – подынтегральное выражение, а – подынтегральная функция.

Если – одна из первообразных для , то , где .

Операцию нахождения неопределённого интеграла от будем называть интегрированием функции .

Если – первообразная для функции , то подынтегральное выражение является дифференциалом функции : .

21.2. Свойства неопределённого интеграла.

1°. .

Доказательство. , то есть знаки d дифференциала и интеграла взаимно сокращаются. ■

2°. .

Доказательство. , то есть знаки интеграла и d дифференциала также взаимно сокращаются, но к нужно добавить некоторую постоянную C. ■

3°. .

4°. .

Доказательство аналогично для случаев 3°, 4°.

и , следовательно формула 3° верна.

и ,

следовательно формула 4° верна. ■

5°. .

Доказательство. . ■

21.3. Таблица интегралов.

Запишем таблицу интегралов, вытекающую из основных формул дифференциального исчисления.

№
1.	0
2.	,
3.	,
4.	, ,
5.
6.
		на интервалах, где подынтегральные функции непрерывны
7.	,
7a.	,
8.
8a.
9.
10.
	,
11.
	,
11a.
12.	,
12a.	,

Справедливость приведённых формул проверяется непосредственно дифференцированием (см. определение 21.1). Например, формула (2) верна, так как 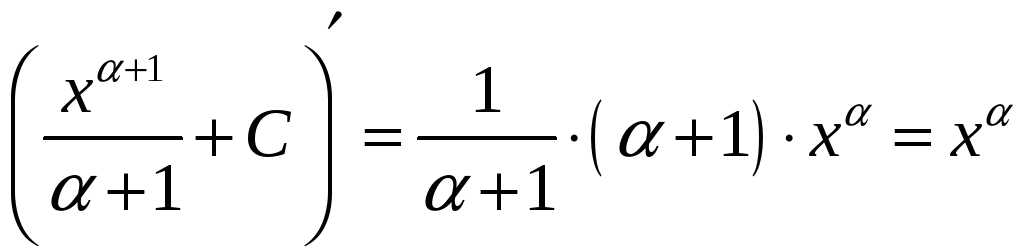равна подынтегральной функции (2).

Докажем (3). Пусть , , тогда . Если же , то и , то есть (3) доказана.

Докажем (11a):

.

С другой стороны, , по теореме 21.2 . Так как , то и .

Формулы 7, 8, 12 докажем позднее.

Таблицу интегралов необходимо пополнять нетривиальными примерами в процессе изучения методов интегрирования. Применяя свойство 5° неопределённого интеграла, можно написать более сложную таблицу интегралов, включающую, например, и т.п. интегралы.

☼ Замечание 21.1. Операция дифференцирования элементарных функций снова приводит к элементарным функциям, операция интегрирования может привести к неэлементарным функциям, то есть к функциям, которые не выражаются через конечное число арифметических операций и суперпозиций элементарных функций. Например, следующие интегралы не интегрируются в элементарных функциях:

– интеграл Пуассона¹,

, – интегралы Френеля²,

– интегральный логарифм,

– интегральный косинус,

– интегральный синус.

Указанные интегралы хотя и существуют, но не являются элементарными функциями. Имеются другие способы для их вычисления. Например, интегральный синус можно представить в виде ряда: так как , то и

. ☼

1 Пуассон Симеон Дени (1781-1840) – французский математик, механик и физик, один из основоположников математической физики.

2 Френель Огюстен Жак (1788-1827) – французский физик и математик.

105