Лекции / 8

8.Интервальные оценки. Доверительные интервалы для МО в случ. норм. распред-я. Доверит. инт-ы для дисперсии в случ. норм.распр. Примеры.

О1: Оценка наз. интервальной., если она хар-ся 2-мя числами: концами интервала внутри кот-го с опред. вер-ю нах-ся знач. параметра.

Интерв. оценки удобны при малом объеме выборки. Пусть это точечн. оценка неизв. параметра . Эта оценка будет тем точнее, чем меньше .

О2:Доверительной вероятностью, обозн. , наз вер-ть, с кот. вып. нер-во. Если доверит. вер-ть выбир. достаточно близко к 1, то число опред. предельн. погрешность точечн. оценки. неизв. парам-ра.

О3: Доверительным интервалом наз инт-л, кот. покрывает параметр с заданной доверит. вер-ю.

Т.к. - СВ, то концы этого инт-ла также случайны. Чем меньше длина инт-ла, тем точнее оценка. Чем б. длина инт-ла, тем оценка мало пригодна для практики.

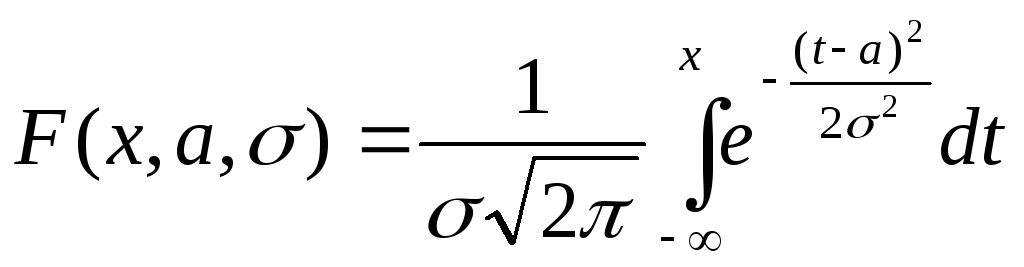, . Это распред-е хар-ся 2-мя параметрами: a-МО, -средн. квадрат. откл-е.

1.Доверит инт. для пар-ра а: Пусть некот. выборка генер. совок-ти, кот распр. норм. треб-ся оценить неизв. МО а. При этом возможны 2 случая:

1сл: изв. В этом случае в качестве статистики выбир ф-ю 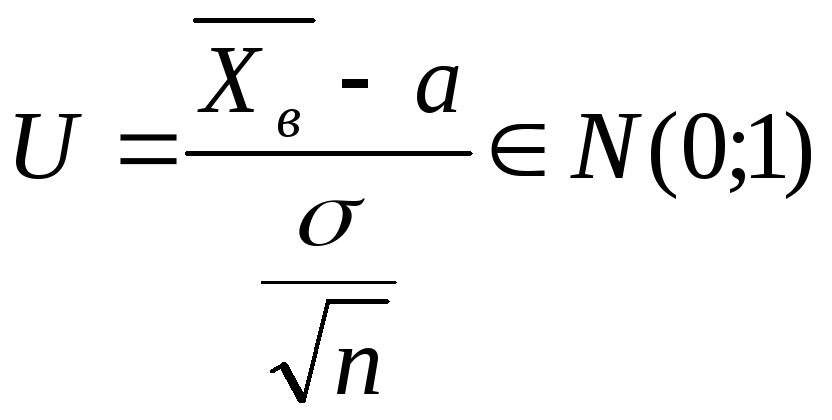. В этом случае при довер. вер-ти довер инт-л для а имеет вид: (1). нах-ся по табл. знач. Лапалса из ур-я . Получ. интервал полностью покрывает МО генер. совок-ти.

Знач-е наз. квантилем данного распр-я. Оценка (1) наз классической. При увелич. объема выборки уменьш., т.е. увел.точность оценки. Увелич-е надежности приводит к увелич. , что уменьш точность оценки.

2сл: неизв. В этом случае все выводы дел-ся на основании выборки. В кач-ве статистики выбир. ф-я 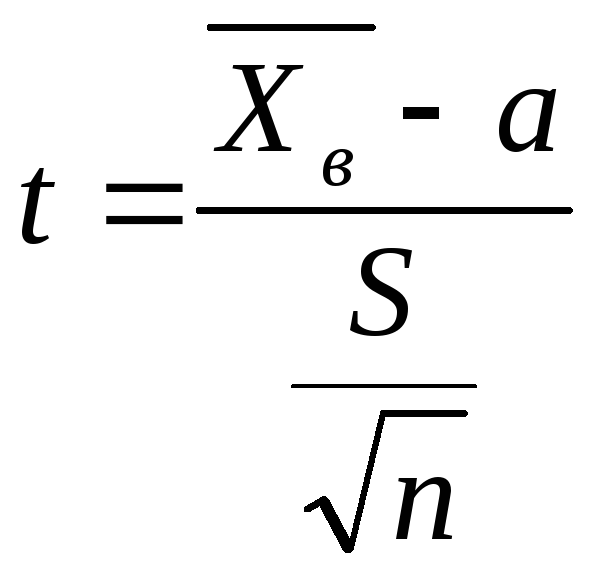, S- выбор.ср. квадр. откл.Тогда доверит. инт-л имеет вид (2). При малых объемах выборки вместо S выбир.. Знач. нах-ся по спец. табл. Если треб. оценить МО с наперед зад-ой точностью , то можно найти объем выборки, при кот. эта точность достиг.

2. Доверит. инт-лы для : При заданной довер. вер-ти довер. интервал для имеет вид(3), S-испр. выб. средн. квадр. откл.Знач. функции нах-ся по спец. табл.

Пусть провод-ся n незав. равноточных измер-й некот. физ вел, точное знач-е кот-й неизвестно.Рассматривая отдельные измерения, как независ СВ, имеющ-е одно и тоже распред-е(как правило, нормальное)с помощью ф-л (1)и(2)можно оценить истинное знач-е неизв-й величины.Это МО а. В теории ошибок точность принято характеризовать с помощью ср. квадр.откл-я случ. ошибок измер-я. Оценивают ее с помощью ф-лы (3).