
- •1. Первообразная. Неопределённый интеграл
- •Вопросы для самопроверки.
- •2. Свойства неопределённого интеграла.
- •Вопросы для самопроверки.
- •3. Внесение функции под знак дифференциала
- •Вопросы для самопроверки.
- •4. Метод замены аргумента
- •Вопросы для самопроверки
- •5. Интегрирование по частям. Рекурре;´нтные4формулы
- •Вопросы для самопроверки.
- •6. Интегрирование рациональных5дробей
- •Вопросы для самопроверки.
- •7. Интегрирование иррациональных7функций
- •Вопросы для самопроверки.
- •8. Интегрирование тригонометрических выражений
- •Вопросы для самопроверки.
- •9. Нахождение неопределенных интегралов с помощью справочника
- •Ответы к примерам из вопросов для самопроверки
Вопросы для самопроверки.
1. Что такое универсальная тригонометрическая подстановка?
2. Как
выражаются
 ,
, ,
, и
и через тангенс половинного угла?
через тангенс половинного угла?
3. Покажите, что
а)
 8.3)
8.3)
б)  (8.4)
(8.4)
4. Вычислите 
5. Вычислите 
6. Вычислите 
9. Нахождение неопределенных интегралов с помощью справочника
Техника интегрирования гораздо сложнее техники нахождения производных, т.е. дифференцирования. Здесь мало помнить основные (табличные) формулы и свойства неопределённого интеграла – надо ещё знать различные рациональные приёмы. Для упрощения вычислений следует использовать справочники [2], [3] для студентов вузов. Существуют и гораздо более подробные справочники, например [4].
Прежде чем приступать к решению примеров с помощью справочника, необходимо (для уверенной ориентации) ознакомиться с его структурой, т.е. с тем, каким образом произведена в нем разбивка формул на группы. У учащихся может возникнуть вопрос: зачем же мы изучаем различные приёмы интегрирования, если существуют справочники? Ответ на этот вопрос очень прост: студент, не знающий основных приёмов интегрирования, не сумеет преобразовать встретившийся интеграл к тому виду, который надо искать в справочнике. Таким образом, для студента, не усвоившего основных приёмов интегрирования, справочник много пользы не принесет.
Для
примера попробуем вычислить по справочнику
[2] интеграл
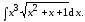
Такого интеграла в справочнике нет. Преобразуем его к виду
 Положим
Положим


Тогда


Остается воспользоваться соответственно формулами под номерами (188), (187), (186) и (185) из таблицы неопределённых интегралов, опубликованной в ряде стереотипных изданий справочника [2].
Ответы к примерам из вопросов для самопроверки
Раздел 1.
6. 
Раздел 2.
2. а) 
б) 
3.  ,
|a|
1.
,
|a|
1.
5. 
Раздел 3.
1. 
2.

3.

4.

5.

6.

Раздел 4.
3.

4.

Обозначим
 тогда
тогда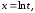

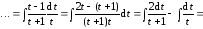

5. а)

Обозначим
 тогда
тогда
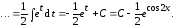
б)

Обозначим
 тогда
тогда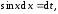

в)

Обозначим
 тогда
тогда


г)
 Обозначим
Обозначим
тогда
 и
и

Раздел 5.
3.

С
учётом известного соотношения
 имеем
имеем

6.

Раздел 6.
5.


где
 и
и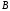 − неизвестные коэффициенты.
− неизвестные коэффициенты.
Методом неопределённых коэффициентов находим, что
 ,
,  тогда
тогда

6.



Раздел 7.
1.

Положим
 тогда
тогда



2.





3.



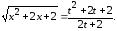



4. 




Раздел 8.
3. а)  Используем универсальную
тригонометрическую подстановку
Используем универсальную
тригонометрическую подстановку
б)  С учётом результата решения предыдущего
примера
С учётом результата решения предыдущего
примера
4. 

5. 



6.


СПРАВОЧНАЯ ТАБЛИЦА
ОСНОВНЫХ НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1.  ,
где
,
где . (2.7)
. (2.7)
2.  ,
где
,
где .
(2.8)
.
(2.8)
3.  . (2.9)
. (2.9)
4.  ,
где
,
где .
(2.10)
.
(2.10)
5.  .
(2.11)
.
(2.11)
6.  .
(2.12)
.
(2.12)
7.  .
(2.13)
.
(2.13)
8.  .
(2.14)
.
(2.14)
9.  .
(2.15)
.
(2.15)
10.  .
(2.16)
.
(2.16)
11.
 .
(4.2)
.
(4.2)
12.
 .
(4.5)
.
(4.5)
13.
 .
(4.6)
.
(4.6)
14.
 .
(5.2)
.
(5.2)
15.  .
(5.4)
.
(5.4)
16. 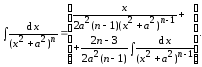
 (5.8)
(5.8)
17.  (6.1)
(6.1)
18.  (6.2)
(6.2)
19.
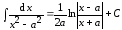 .
(6.3)
.
(6.3)
20.
 .
(7.12)
.
(7.12)
21.
 .
(7.13)
.
(7.13)
22.
 .
(8.3)
.
(8.3)
23.  . (8.4)
. (8.4)
Библиографический список
1.Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.: Учебник для вузов, Том 2: Дифференциальное и интегральное исчисление. – М.: Дрофа – 2010. – 509 с.
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инжене-ров и учащихся втузов. – М.: Издательство «Наука», 1980. – 976 с.
3. Выгодский М.Я. Справочник по высшей математике. – М.: Издательство «Наука», 1964. – 871 с.
4. Градштейн И.С., Рыжик Н.С. Таблицы интегралов, сумм и произведений. М.: Наука, 1963.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я., Данко С.П. Высшая математи-ка и упражнения в задачах: Учебное пособие для вузов. В 2 частях. Часть 1. – М.: ООО «Издательство Оникс», «Издательство „Мир и образование“» – 2009. – 368 с.
6. Лузин Н.Н. Интегральное исчисление. – М.: Государственное издатель-ство «Советская наука» – 1953. – 416 с.
7. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая матема-тика для экономических специальностей: Учебник и практикум. – М.: Высшее образование, 2008 – 893 с.
8. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учебник для втузов. В 2-х т., Т.1: - М.: Интеграл–Пресс, 2009. – 416 с.
9. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис-пресс, для втузов. В 2-х т., Т.1: - М.: Интеграл–Пресс, 2009. – 416 с.
10. Фихтенгольц Г.М. Основы математического анализа. В 2-х т., Том 1. – М.: Издательство «Наука», 1968. – 440 с.
11. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей матема-тики (в двух томах). Т.1Учеб. пособие для вузов. – М.: Издательство «Высшая школа», 1978. – 384 с.
1 Дифференцированием функции называется операция нахождения её производной.
2 Обозначение происходит от латинского слова constanta – ‛постоянная’.
3Необходимо обратить внимание на то, что второй гласной буквой в этом слове является «ы», а не «и», что соответствует последней редакции правил русского правописания.
4 Обозначение происходит от латинского слова recurrens – ‛возвращающийся’.
5 Рациональное выражение – алгебраическое выражение, не содержащее радикалов. «Радикал» - от позднелатинского слова radicalis – ‛имеющий корни’. Латинское radix - ‛корень’.
6 Дробь считается правильной, когда степень многочлена, стоящего в числителе, ниже степени многочлена, стоящего в знаменателе.
7 Иррациональное выражение – алгебраическое выражение, содержащее радикалы. См. также сноску 6.
