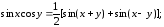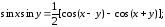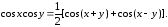- •1. Первообразная. Неопределённый интеграл
- •Вопросы для самопроверки.
- •2. Свойства неопределённого интеграла.
- •Вопросы для самопроверки.
- •3. Внесение функции под знак дифференциала
- •Вопросы для самопроверки.
- •4. Метод замены аргумента
- •Вопросы для самопроверки
- •5. Интегрирование по частям. Рекурре;´нтные4формулы
- •Вопросы для самопроверки.
- •6. Интегрирование рациональных5дробей
- •Вопросы для самопроверки.
- •7. Интегрирование иррациональных7функций
- •Вопросы для самопроверки.
- •8. Интегрирование тригонометрических выражений
- •Вопросы для самопроверки.
- •9. Нахождение неопределенных интегралов с помощью справочника
- •Ответы к примерам из вопросов для самопроверки
Вопросы для самопроверки.
1. Сформулируйте теорему о разложении многочлена на простейшие множители.
2. Что такое рациональная дробь? Что такое правильная рациональная дробь?
3. Изложите право разложения правильной рациональной дроби на простейшие в случае:
а) простых действительных корней знаменателя,
б) действительных кратных корней знаменателя,
в) когда среди корней знаменателя имеются пары простых комплексно-сопряжённых корней,
г) когда среди корней знаменателя имеются пары кратных комплексно-сопряжённых корней.
4. Поясните идею метода неопределённых коэффициентов.
5. Покажите, что
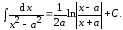 (6.3)
(6.3)
6. Вычислите
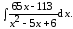
7. Интегрирование иррациональных7функций
Рассмотрим метод вычисления интегралов вида
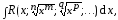 (7.1)
(7.1)
где
символ R
означает рациональное выражение от
аргумента, указанного в круглых скобках;
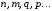 - целые числа.
- целые числа.
Здесь
целесообразно воспользоваться
подстановкой
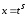 ,
где
,
где - общий знаменатель дробей
- общий знаменатель дробей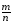 и
и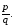 При этом подынтегральное выражение
приводится к рациональной функции от
переменной
При этом подынтегральное выражение
приводится к рациональной функции от
переменной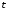
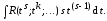 (7.2)
(7.2)
Рассмотрим теперь метод вычисления интегралов вида
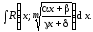 (7.3)
(7.3)
Для дробно-рациональной функции введём обозначение
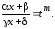 (7.4)
(7.4)
Тогда
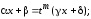
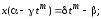
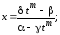
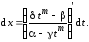 (7.5)
(7.5)
Пример
1. 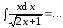
Пусть 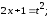
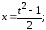
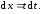
Тогда
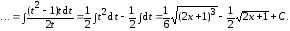
Пример
2. 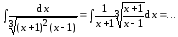
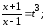
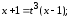
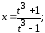
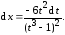
Пусть 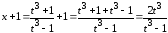 .
.
В результате преобразования получим интеграл от рациональной дроби
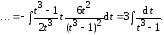
Теперь рассмотрим метод вычисления интегралов вида
 (7.6)
(7.6)
Здесь
будем различать два случая: когда
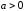 и
и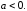
Случай
1 (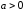 ).
).
Сделаем
замену (подстановку)
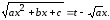 (7.7)
(7.7)
Тогда
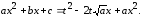
Взаимно
уничтожая
 в левой и правой частях равенства,
получаем
в левой и правой частях равенства,
получаем
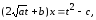
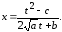 (7.8)
(7.8)
Подставим
выражение (7.8) для х
как функцию
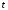 в (7.7)
в (7.7)
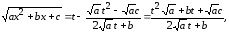 (7.9)
(7.9)
т.е. подынтегральная функция (и интегральное выражение) становится рациональной функцией относительно переменной t.
Случай
2
(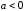 ). При
этом квадратный трёхчлен
). При
этом квадратный трёхчлен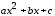 либо отрицателен при всех значениях
либо отрицателен при всех значениях (в случае комплексных корней), либо имеет
действительные корни.
(в случае комплексных корней), либо имеет
действительные корни.
В дальнейшем будем рассматривать только последний случай. Представим подкоренное выражение в следующем виде
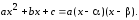
Введём подстановку
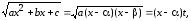 (7.10)
(7.10)

После преобразований получим
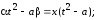
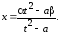
Поставим в (7.10)
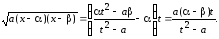
Таким
образом, и в этом случае получена
возможность рационального представления
подынтегрального выражения через
параметр

Пример
3 (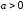 ).
).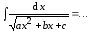
Используем соотношения (7.8) и (7.9). Дифференцируя обе части выражения (7.8) получим
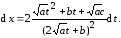 (7.11)
(7.11)
Подставляя (7.9) и (7.11) в исходный интеграл, получим

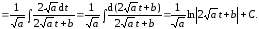
Окончательно
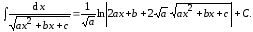 (7.12)
(7.12)
Вопросы для самопроверки.
1. Вычислите 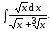
2. Вычислите 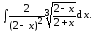
3. Вычислите 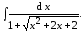
4. Вычислите 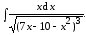
5. Полагая
в (7.12)
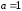 и
и покажите, что
покажите, что
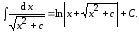 (7.13)
(7.13)
8. Интегрирование тригонометрических выражений
Рассмотрим
интеграл вида
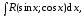 (8.1)
(8.1)
где
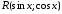 - рациональная функция от
- рациональная функция от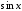 и
и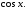
В общем случае интеграл вида (8.1) всегда может быть приведен к интегралу от рациональной алгебраической функции с помощью универсальной тригонометрической подстановки
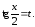 (8.2)
(8.2)
При этом

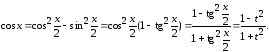
Так
как 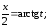
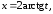 то
то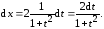
Пример 1.
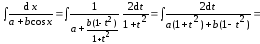
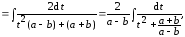
т.е. получили интеграл «арктангенсного» типа (см. (4.2)).
В некоторых случаях интегралы вида (8.1) берутся проще другими приёмами:
1.
Если подынтегральная функция
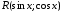 меняет свой знак при замене
меняет свой знак при замене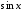 на
на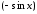 ,
то подынтегральное выражение приводится
к рациональной дроби подстановкойt
= cos
x
,
то подынтегральное выражение приводится
к рациональной дроби подстановкойt
= cos
x
Пример 2.
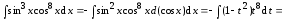
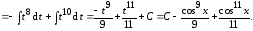
2.
Если при замене
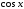 на
на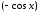 подынтегральная функция меняет знак,
то следует делать замену переменной
подынтегральная функция меняет знак,
то следует делать замену переменной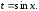 Пример можно подобрать самостоятельно
(или см. вопрос 5 для самопроверки).
Пример можно подобрать самостоятельно
(или см. вопрос 5 для самопроверки).
3.
Если при одновременной замене
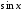 на
на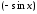 и
и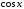 на
на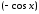 подынтегральная функция не меняет
знака, то следует делать замену переменной
подынтегральная функция не меняет
знака, то следует делать замену переменной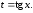
Пример 3.
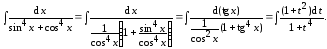
В итоге преобразований получили интеграл от рациональной дроби.
Прежде чем использовать вышеперечисленные способы интегриро-вания рациональных выражений от тригонометрических функций, имеет смысл попробовать преобразовать подынтегральную функцию с целью получения интегралов от более простых выражений.
Пример 4.
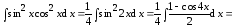
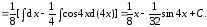
Пример 5.
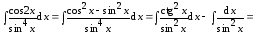
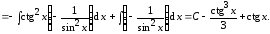
В вычислении интегралов вида
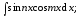
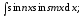
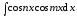
подынтегральные произведения следует представить в виде сумм