Матан / Четвёртый блок вопросов

Вопросы к разделу «Интегральное исчисление функции одной переменной»

1. Первообразная: определение, две теоремы о первообразной.

2. Неопределённый интеграл: определение, свойства.

3. Таблица неопределённых интегралов.

4. Основные приёмы интегрирования: подведение под знак дифференциала, интегрирование по частям (на примерах).

5. Определенный интеграл :

• интегральная сумма для ;

• определение , необходимое условие существования;

• свойства (особенное внимание теореме о среднем).

6. Теорема Барроу (с доказательством).

7. Формула Ньютона – Лейбница (вывод).

8. Геометрический смысл определённого интеграла.

9. Стандартные формулы для вычисления длины линии, площади плоской фигуры, объёма тела вращения с помощью определённого интеграла (вывод этих формул).

10. Решение с использованием определённого интеграла конкретных физических задач (на примерах).

11. Несобственный интеграл первого рода: определение, необходимое условие сходимости. Главное значение

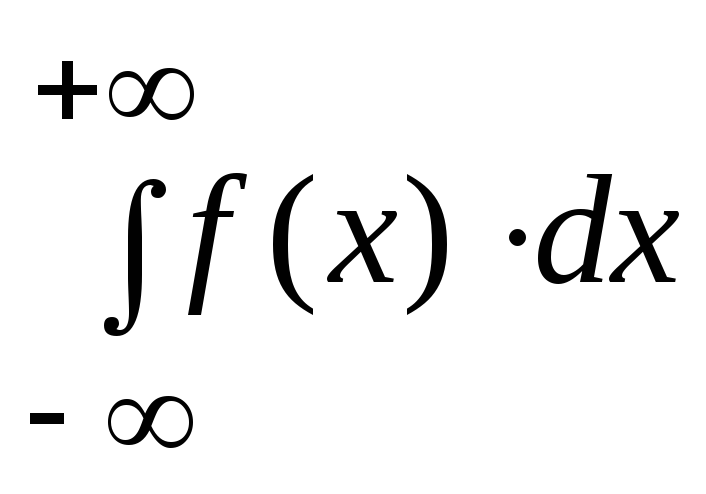
12. Сходимость интеграла .

13. Признаки сравнения сходимости несобственных интегралов первого рода.

14. Несобственный интеграл второго рода: определение.

15. Сходимость интеграла или при .

16. Признаки сравнения сходимости несобственных интегралов второго рода.

Образцы стандартных примеров по разделу «Интегральное исчисление»

• Найти , , , , , , .

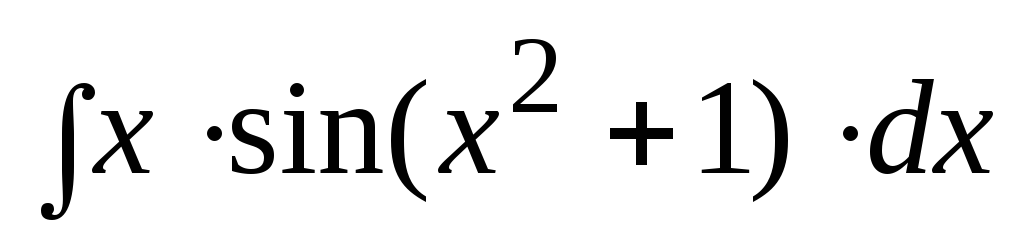• Вычислить по формуле Ньютона - Лейбница .

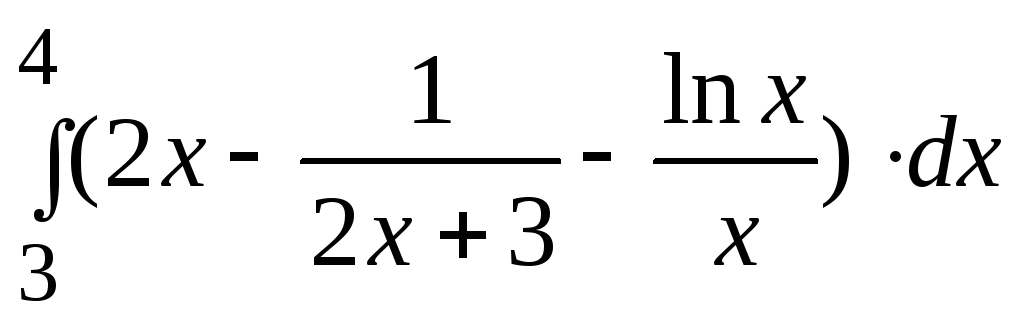• Построить какую-нибудь интегральную сумму при для .

• Найти объём, полученный вращением участка линии при вокруг оси .

• Найти площадь, ограниченную линиями , , .

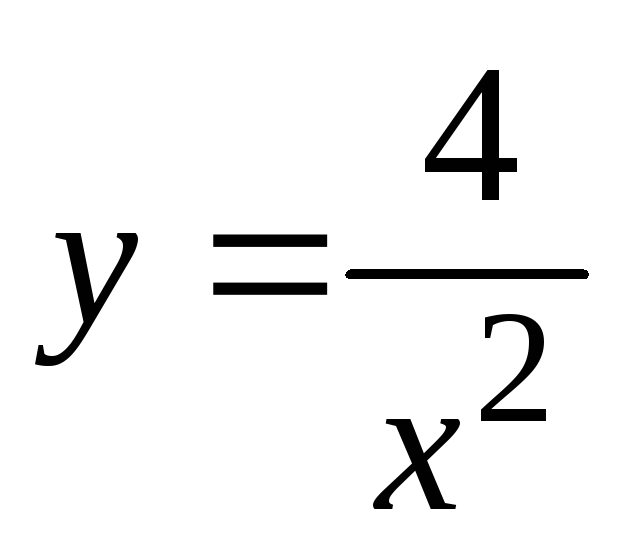• Составить интеграл (не вычисляя его), равный длине дуги замкнутой линии .

• Составить интеграл (не вычисляя его), равный длине участка линии 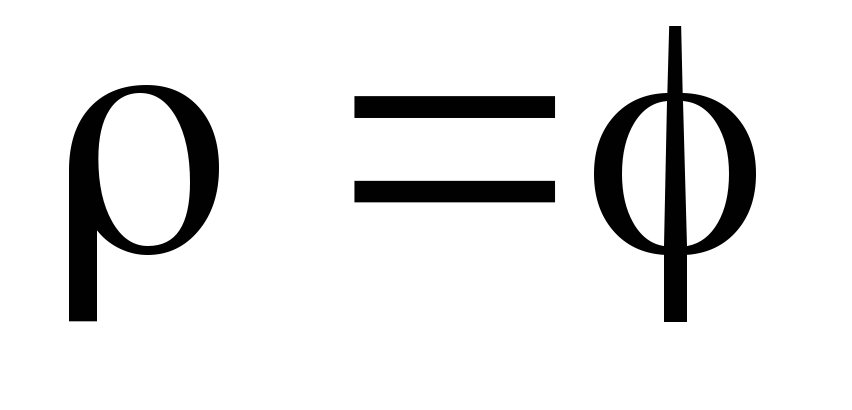при (координаты полярные).

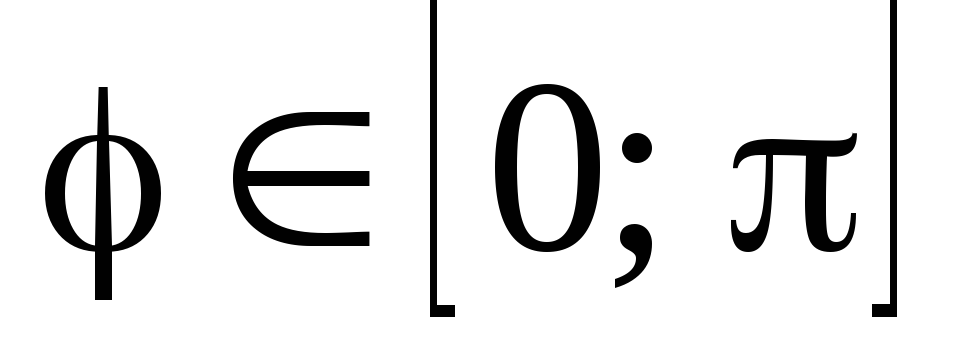• Найти площадь, ограниченную линией и участком линии при (координаты полярные).

• Указать, какие из интегралов , , , , . являются несобственными. Исследовать их сходимость.

Вопросы к разделу «Некоторые сведения из ТФКП»

1. Изображение числа на плоскости. , . Тригонометрическая форма записи числа .

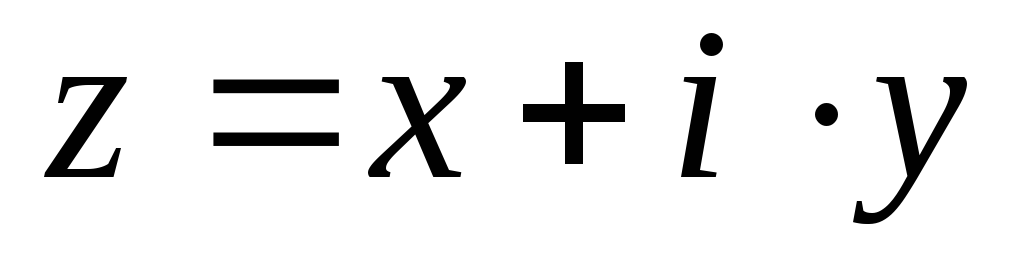2. Формула Эйлера. Показательная форма записи числа .

3. Вычисление значений для любого целого , положительного или отрицательного.

4. Алгебраические действия с комплексными числами в алгебраической или показательной форме.

5. Вычисление значений элементарных функций от переменной .

Образцы стандартных примеров по разделу Некоторые сведения из ТФКП:

• Изобразить на плоскости и записать в показательной форме: , , , , .

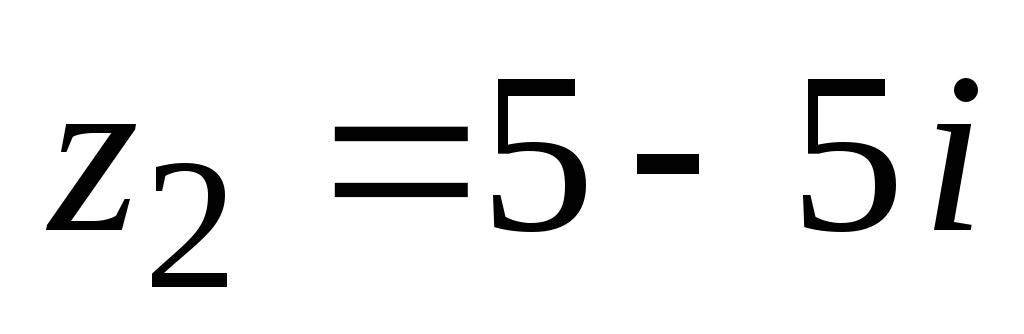• Вычислить: ; ; ; .

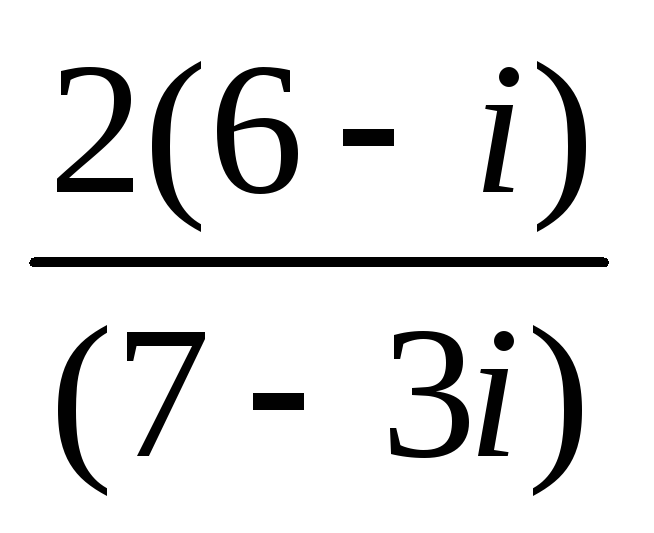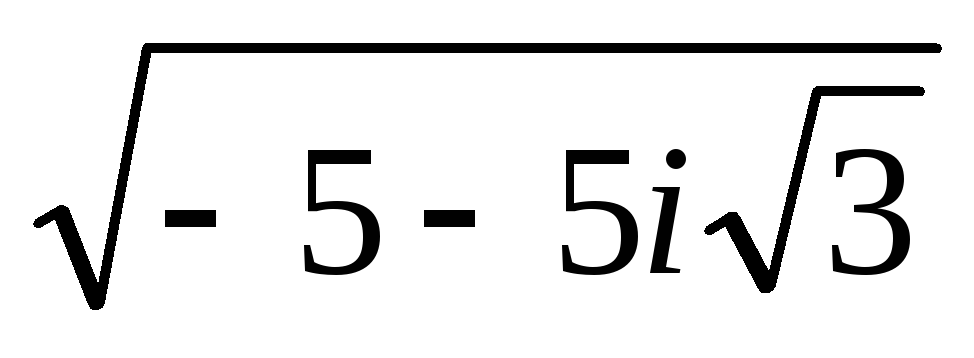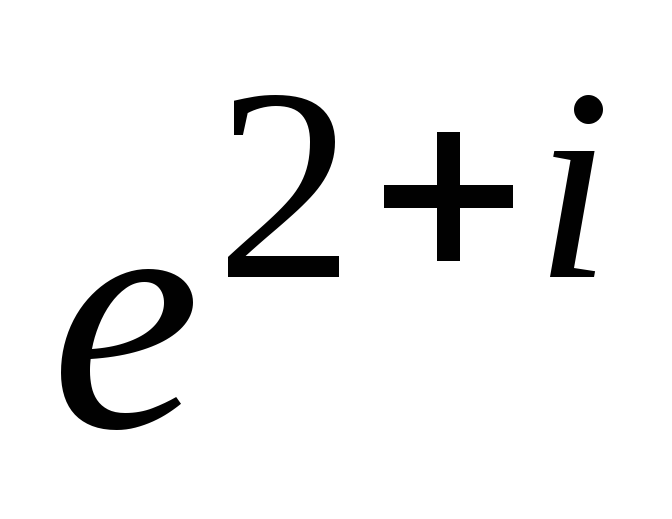• Вычислить: , .

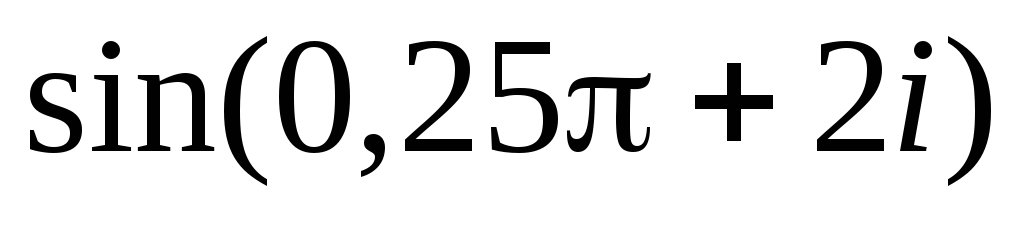Вопросы к разделу «Ряды»

1. Частичная сумма для числового ряда 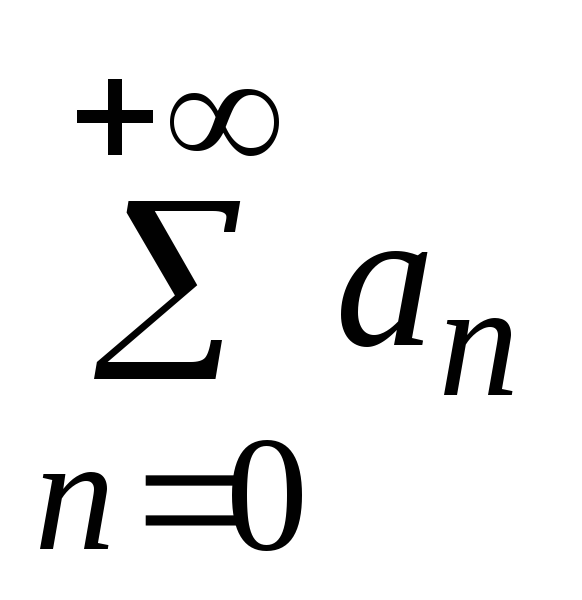. Определение . Сходящиеся и расходящиеся ряды.

2. Необходимый признак сходимости числового ряда .

3. Интегральный признак Коши сходимости числового ряда с положительными слагаемыми ( для ).

4. Гармонический ряд. Обобщённый гармонический ряд. Сходимость гармонического и обобщённого гармонического рядов .

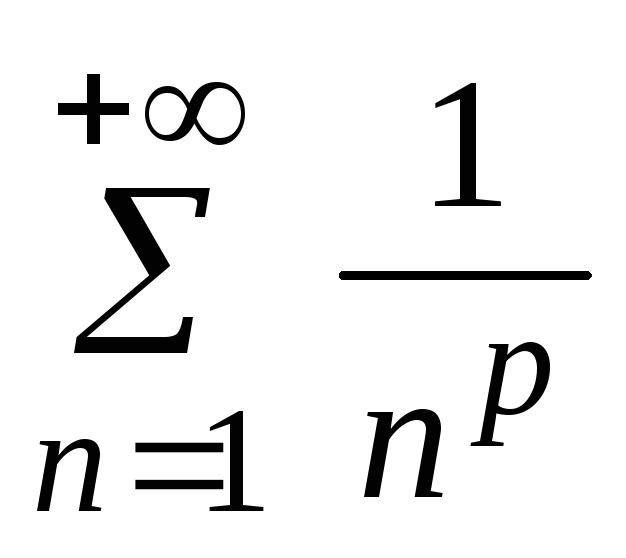5. Признаки сравнения сходимости знакоположительных рядов.

6. Знакопеременные числовые ряды. Абсолютная и условная сходимость.

7. Признак Даламбера (д’Аламбера) абсолютной сходимости ряда.

8. Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов.

9. Оценка погрешности при замене частичной суммой (на примерах).

10. Функциональные ряды . Область сходимости функционального ряда.

11. Степенные ряды . Структура области сходимости степенного ряда. Радиус сходимости степенного ряда.

12. Ряды Тейлора и Маклорена для функции 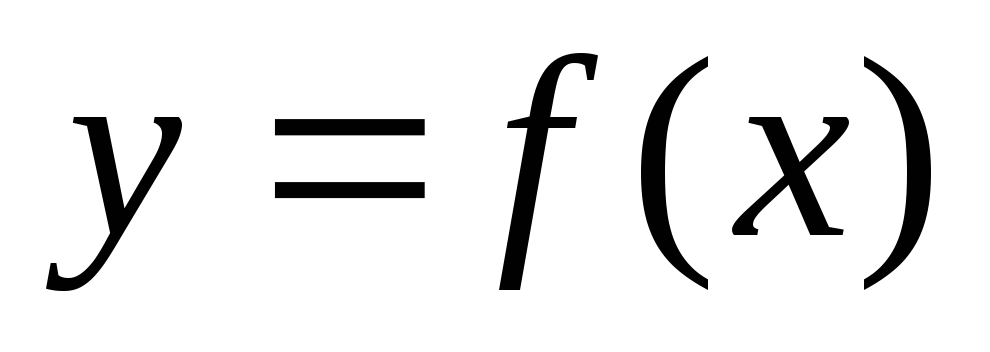. Достаточное условие выполнения равенства .

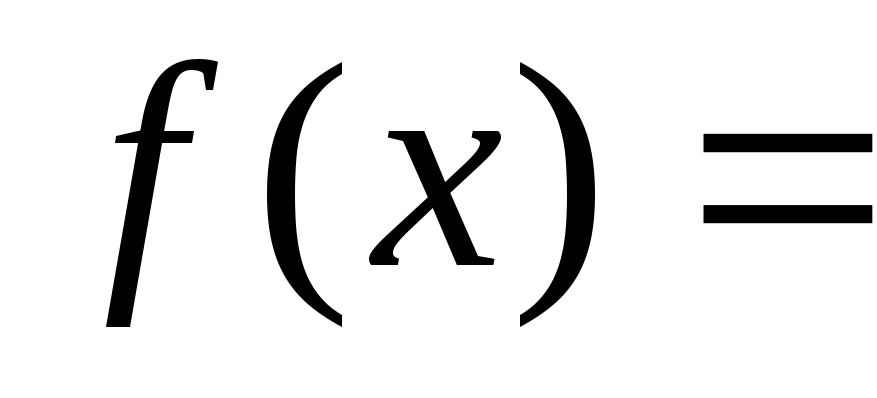
13. Ряды Маклорена для функций .

14. Использование рядов в приближённых вычислениях (с оценкой погрешности, на примерах).

Образцы стандартных примеров по разделу Ряды:

• Дан ряд (или , или и т.п.) Найти сумму первых четырёх слагаемых. Исследовать сходимость ряда.

• Найти область сходимости степенного ряда.

• Разложить функцию в ряд Тейлора в окрестности точки (или функцию в окрестности точки и т.п.). Указать область сходимости ряда.

• Вычислить приближённо ( или и т.п.) (с погрешностью не более 1%), используя разложение подынтегральной функции в ряд.

Вопросы к разделу «Дифференциальные уравнения»

1. ДУ (дифференциальное уравнение) первого порядка, общий вид. ДУ первого порядка, разрешённое относительно производной. Общее, частное и особое решения ДУ первого порядка.

2. ДУ с разделяющимися переменными.

3. Линейное ДУ первого порядка.

4. Задача Коши для ДУ первого порядка. Теорема существования и единственности решения задачи Коши.

5. ДУ ого порядка, общий вид. ДУ ого порядка, разрешённое относительно старшей производной. Общее решение, частное решение.

6. Задача Коши для ДУ ого порядка. Теорема существования и единственности решения задачи Коши.

7. Линейно зависимые и линейно независимые функции на 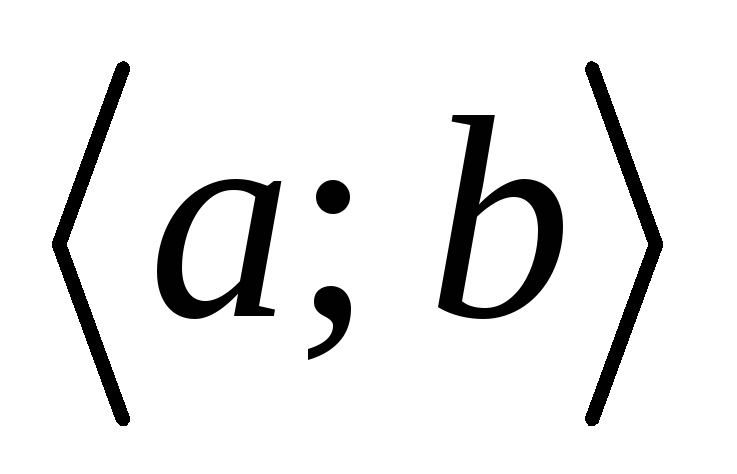. Определитель Вронского.

8. Линейное ДУ ого порядка, однородное и неоднородное. Расшифровка символа .

9. Теорема о структуре общего решения уравнения . Фундаментальная система решений.

10. Теорема о структуре общего решения уравнения .

11. Линейные ДУ ого порядка с постоянными коэффициентами, однородные. Характеристическое уравнение. Вид фундаментальной системы решений в зависимости от значений корней характеристического уравнения.

12. Линейные ДУ ого порядка с постоянными коэффициентами, неоднородные. Метод неопределённых коэффициентов для решения уравнений с правой частью вида (на примерах).

13. Преобразование выражений ) к виду .

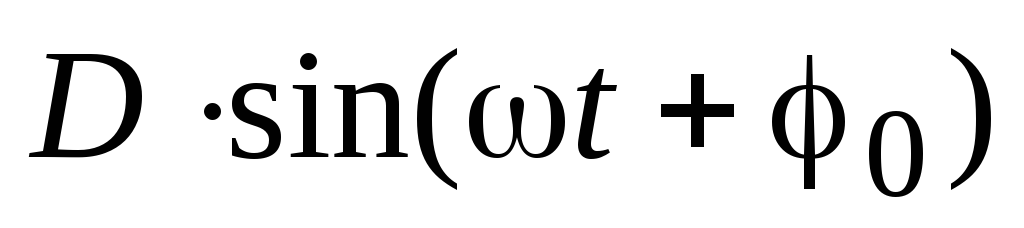Образцы стандартных примеров по разделу Дифференциальные уравнения:

• Найти общее решение уравнения .

• Найти решение задачи Коши , .

• Найти общее решение дифференциального уравнения при , или , или , или и т.п.

• Найти частное решение дифференциального уравнения . Ответ представить в виде .

• Найти частное решение дифференциального уравнения .