
Матан / Третий блок вопросов
.docДифференциальное исчисление функций одной и нескольких переменных.
-
Множества. Операции с множествами. Числовые множества. Точка сгущения числового множества. Изолированная точка числового множества. Замкнутые множества. Функция на числовом множестве. Область определения и изменения функции.
-
Окрестность точки
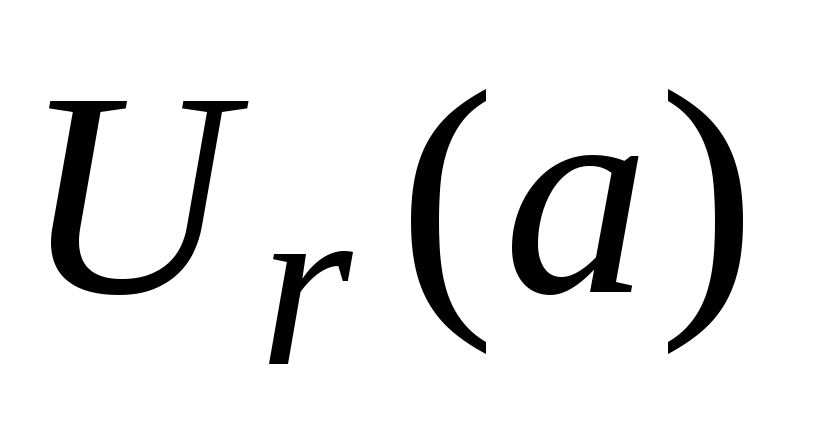 ,
проколотая окрестность
,
проколотая окрестность
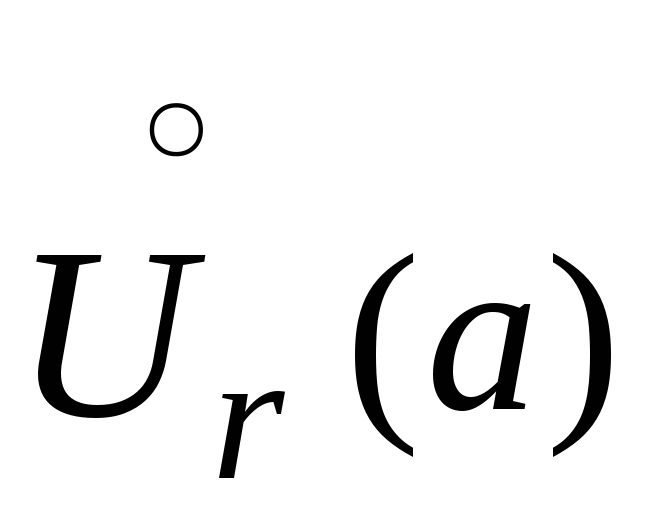 ,
правая окрестность
,
правая окрестность
 ,
левая окрестность
,
левая окрестность
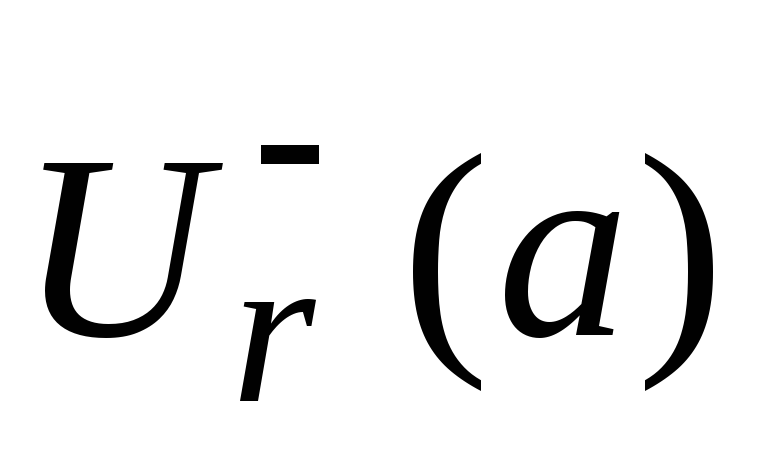 .
Окрестность бесконечно удалённой точки
.
Окрестность бесконечно удалённой точки
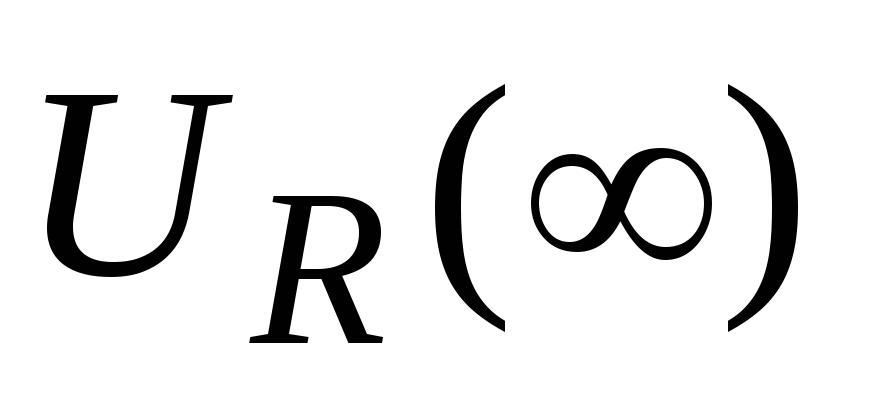 ,
,
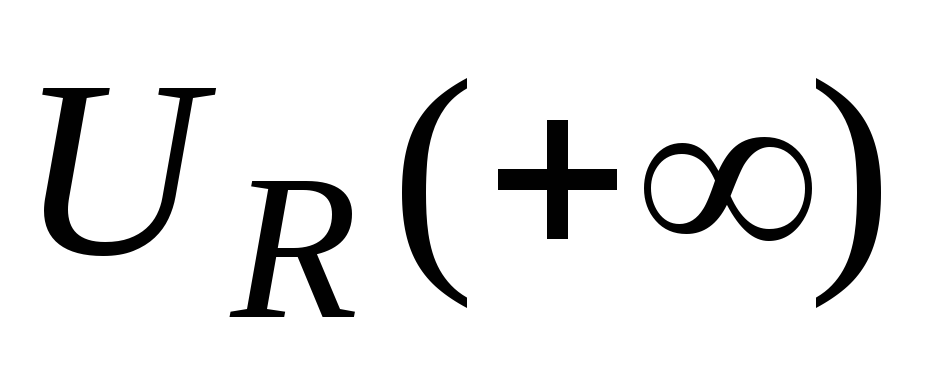 ,
,
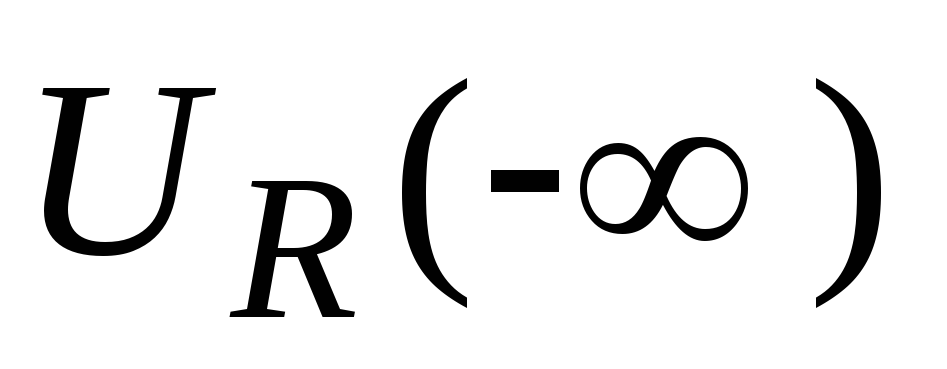 .
. -
Предел функции: определение и графическая иллюстрация. Теоремы о пределах (теоремы о пределе суммы, произведения, теорема о переделе сжатой переменной и т.п.). Понятие неопределенности, список неопределённостей. Односторонние пределы.
-
Раскрытие некоторых неопределённостей с помощью алгебраических преобразований (на примерах).
-
Первый замечательный предел. Второй замечательный предел.
-
Бесконечно малые и бесконечно большие функции (определение). Сравнение бесконечно больших и бесконечно малых функций (эквивалентные функции, функции одного порядка, порядок одной функции относительно другой и т.п.). Главная часть б.б. и б.м. функций.
-
Теорема о замене функции на эквивалентную под знаком предела. Таблица эквивалентных функций. Раскрытие неопределённостей с использованием эквивалентных преобразований (на примерах).
-
Непрерывность функции в точке, определение. Точки разрыва и их классификация. Непрерывность функции на
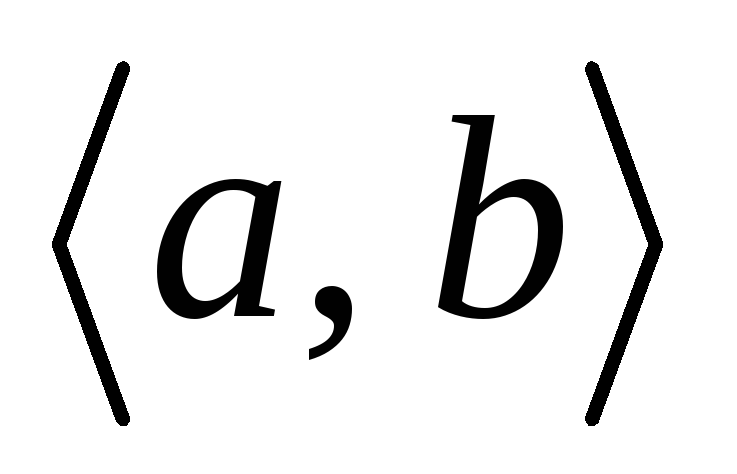 .
. -
Приращение функции в точке. Определение производной. Геометрический смысл производной. Таблица производных. Правила дифференцирования (производная суммы, произведения, производная сложной функции и т.п.).
-
Дифференциал: определение, необходимое и достаточное условие существования, формула для вычисления, геометрический смысл. Инвариантность формы первого дифференциала.
-
Производные и дифференциалы высших порядков.
-
Правило Лопиталя.
-
Условия монотонности функции. Экстремум функции (определение, необходимое условие существования, достаточное условие существования).
-
Выпуклые и вогнутые функции (определение, достаточное условие выпуклости или вогнутости). Точки перегиба.
-
Асимптоты графика функции (определение, алгоритм нахождения).
-
Общая схема исследования функции и построения ее графика. Построение графика (на примерах).
-
Параметрические заданные функции, их производные.
-
Функция нескольких переменных на множестве
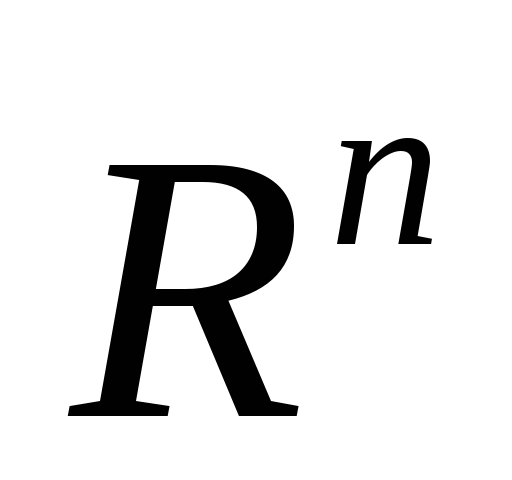 .
Частные производные: определение,
вычисление.
Дифференциал (определение, необходимое
условие существования, формула для
вычисления, инвариантность формы
первого дифференциала).
.
Частные производные: определение,
вычисление.
Дифференциал (определение, необходимое
условие существования, формула для
вычисления, инвариантность формы
первого дифференциала). -
Сложные функции. Производные сложных функций.
-
Частные производные и дифференциалы высших порядков. Формальный оператор
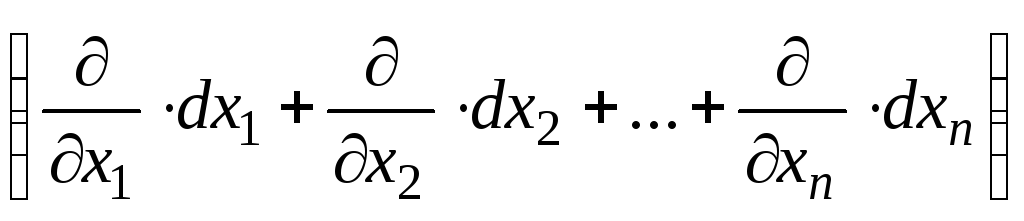 и его использование при вычислении
дифференциалов высших порядков.
и его использование при вычислении
дифференциалов высших порядков. -
Экстремум функций нескольких переменных, определение. Необходимое условие существования экстремума. Достаточное условие существования экстремума.
-
Формальные дифференциальные операторы
 и
и
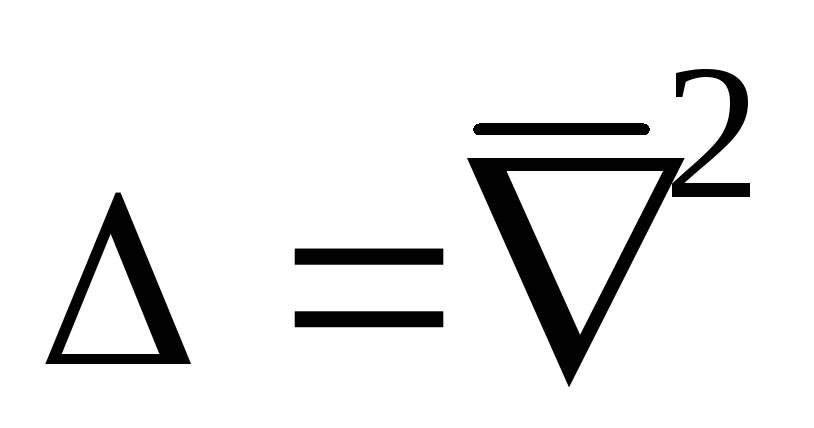 .
Вычисление
.
Вычисление
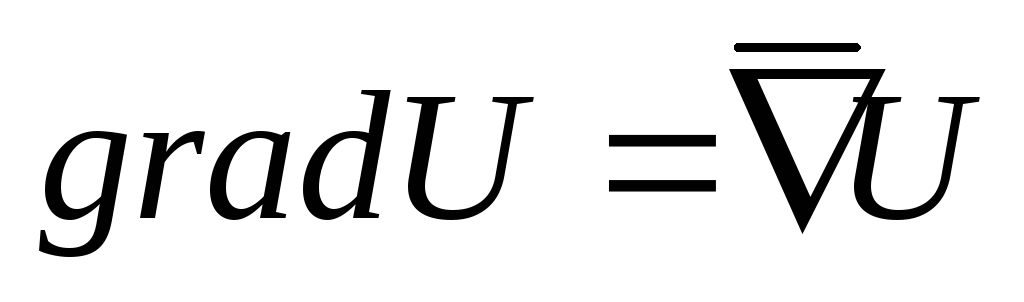 ,
,
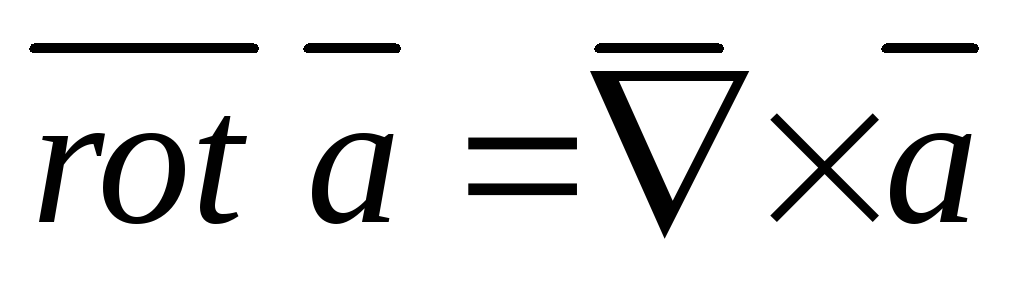 ,
,
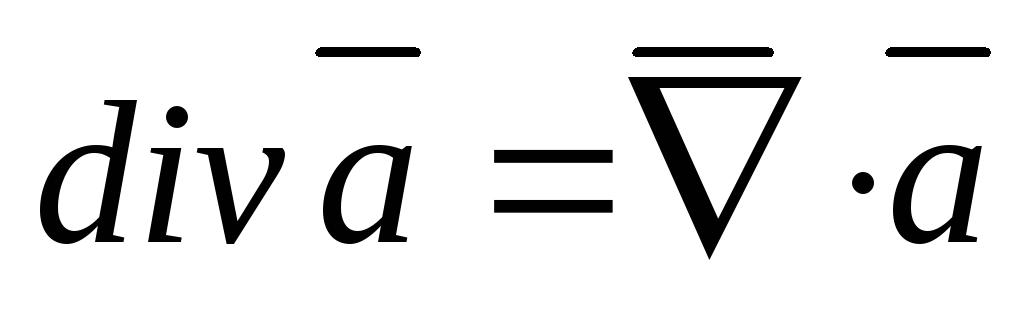 ,
,
 (на примерах).
(на примерах). -
Касательная плоскость и нормаль к поверхности.
Образцы стандартных примеров по разделу Дифференциальное исчисление функций одной и нескольких переменных:
-
Найти
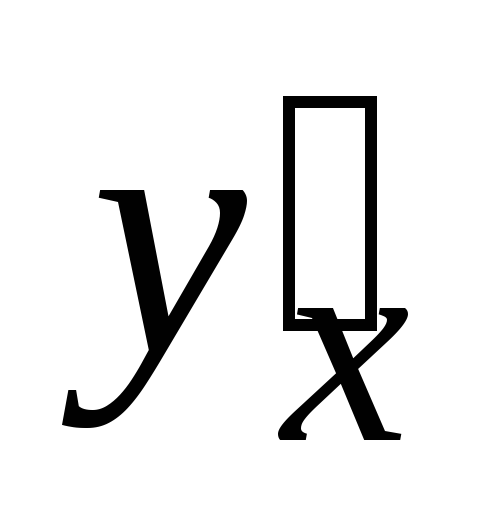 :
:
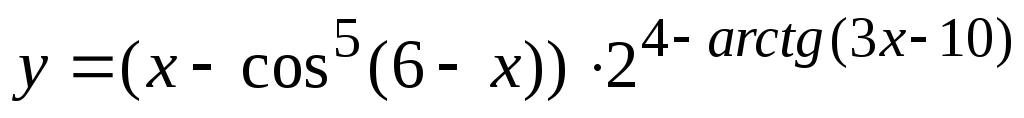 ,
,
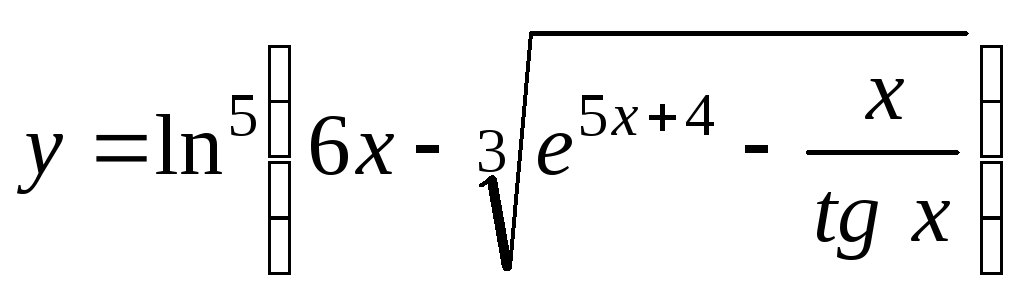 ,
,

-
Найти
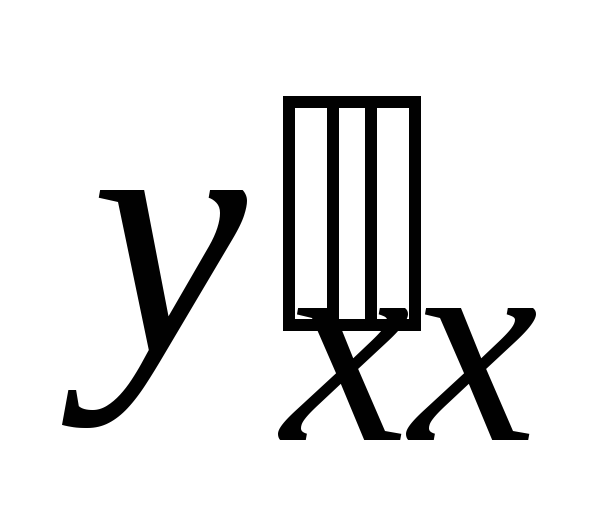 :
:
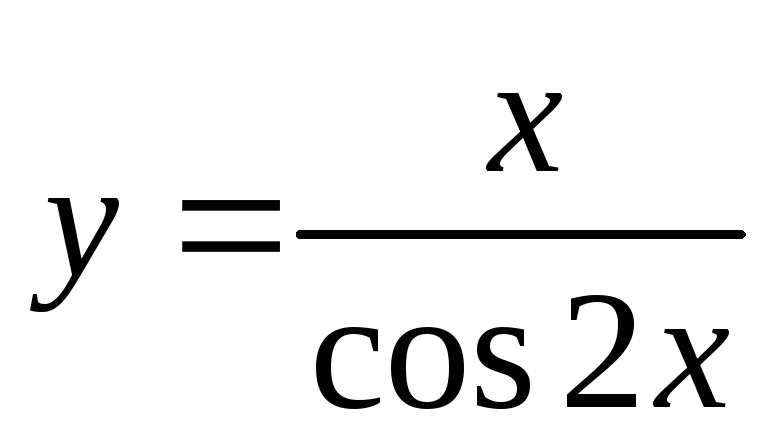 ;
;
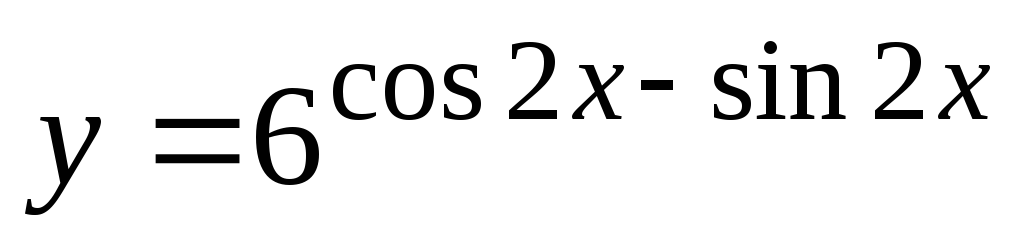 .
.
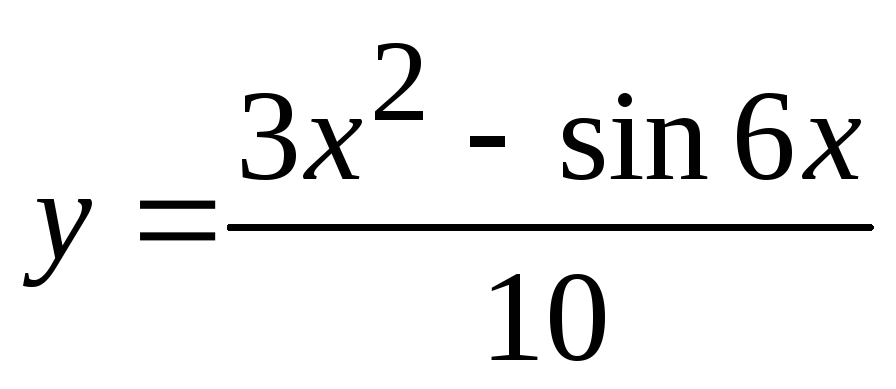 ,
,
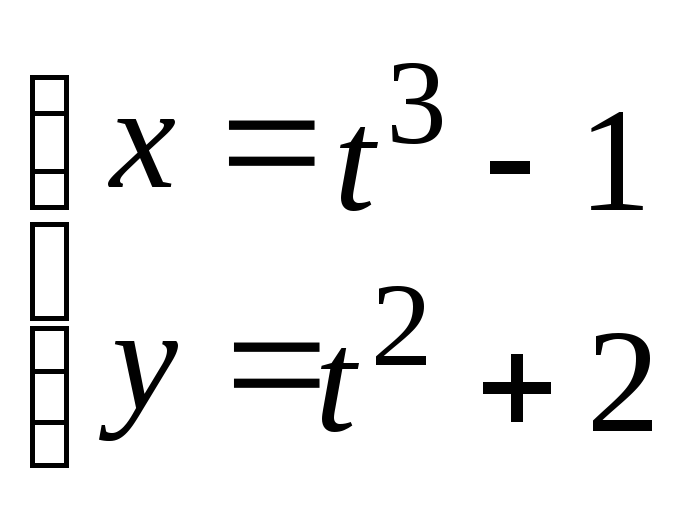 .
. -
Найти
-
Найти
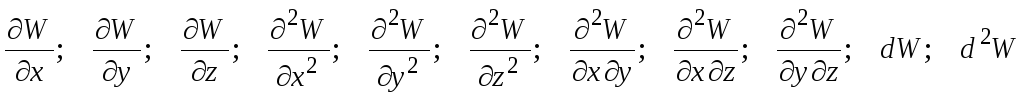 ,
,
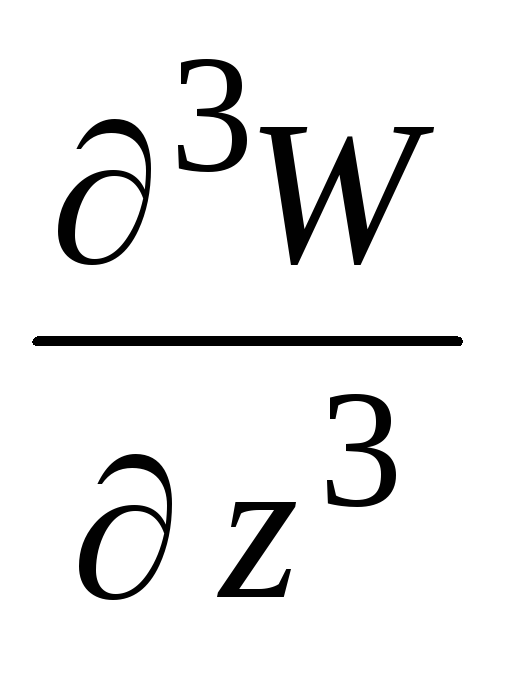 и т.п., если
и т.п., если
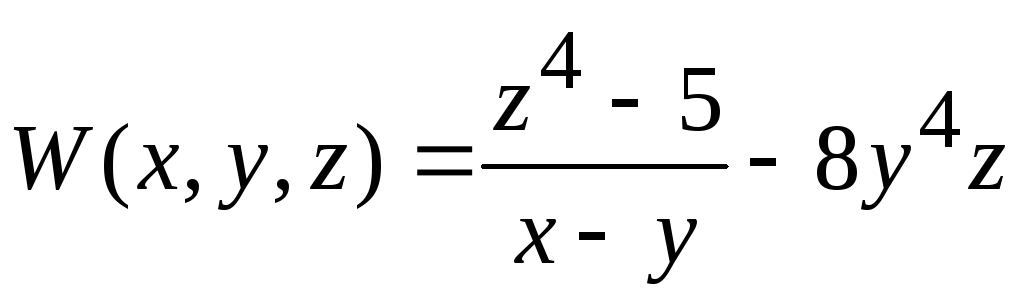 или
или
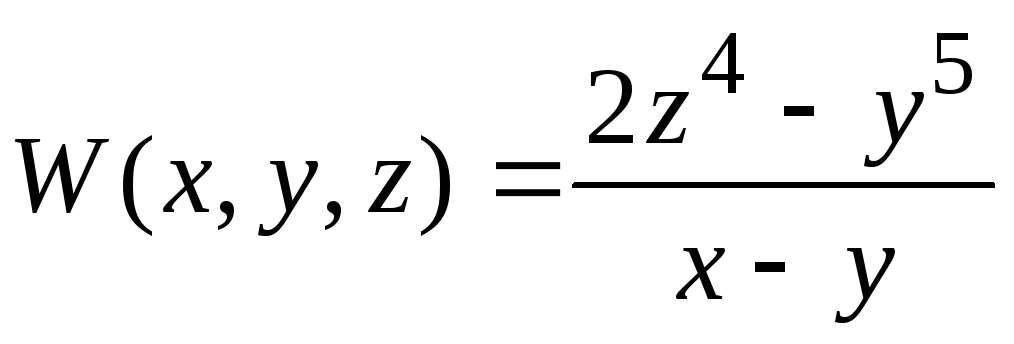 .
. -
Найти
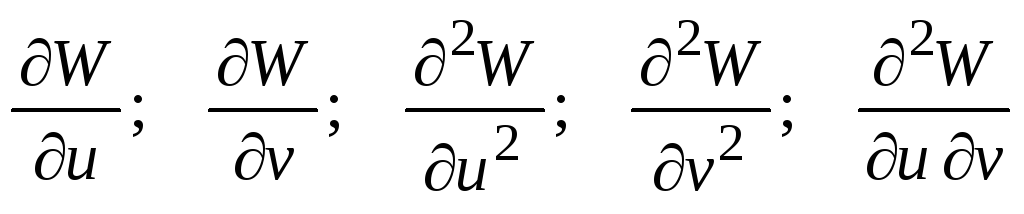 ,
если
,
если
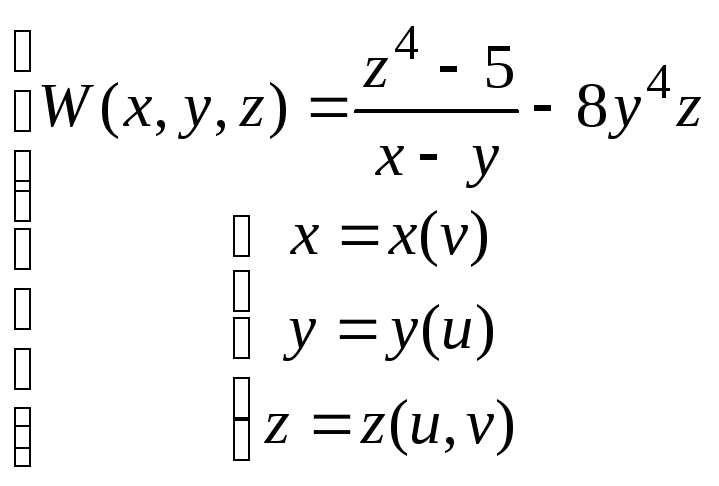 .
. -
Найти
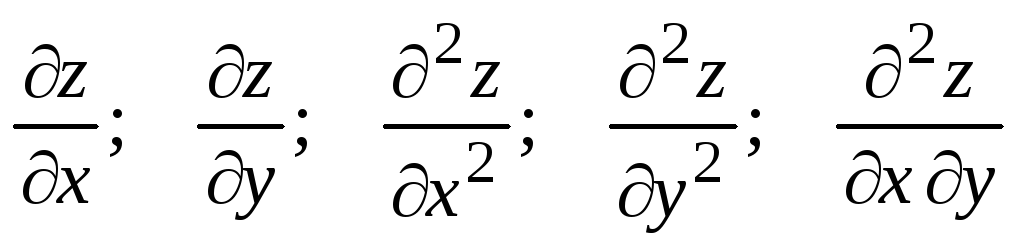 ,
если
,
если
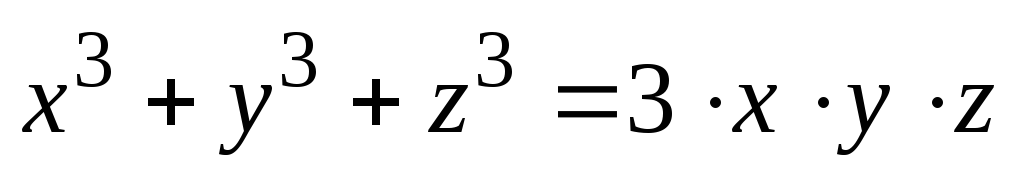 или
или
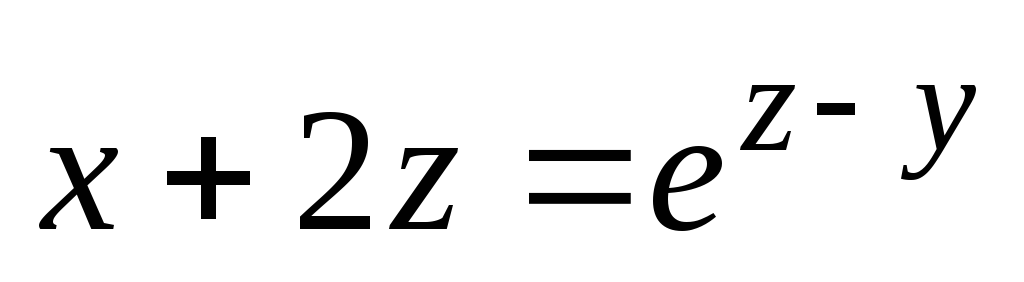 и
т.п.
и
т.п. -
Вычислить, не пользуясь правилом Лопиталя:
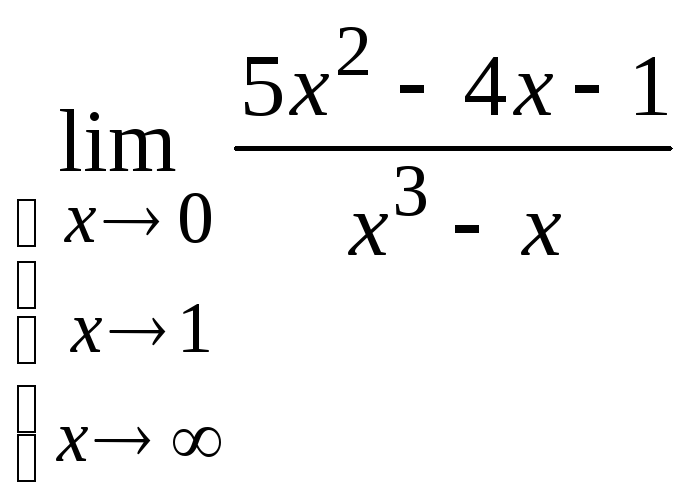 .
. -
Вычислить (в случае необходимости использовать правило Лопиталя).
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
-
Построить график функции
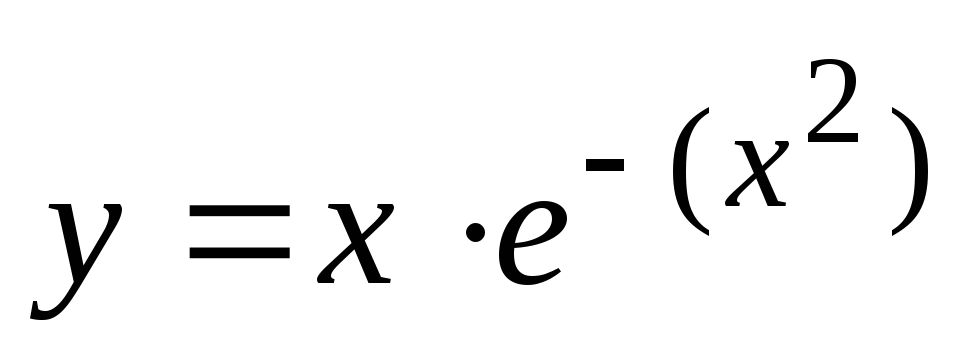 .
. -
Найти экстремумы функций:
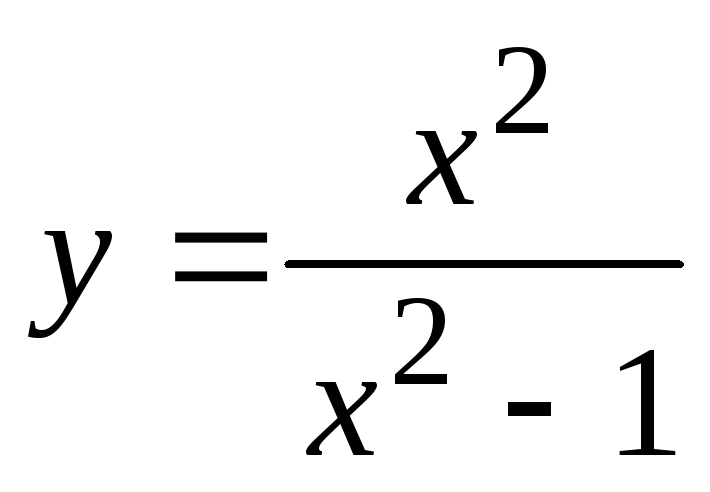 ;
;
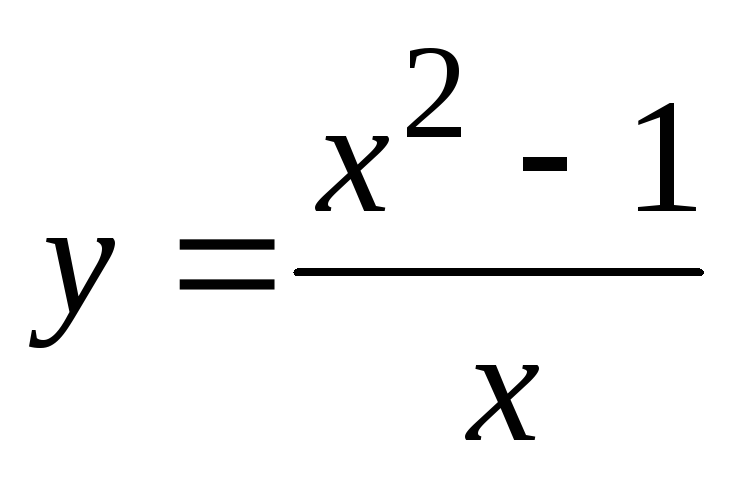 ;
;
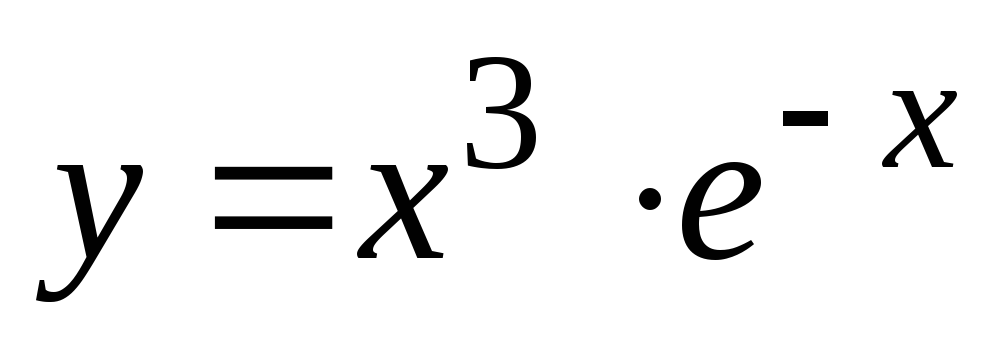 .
. -
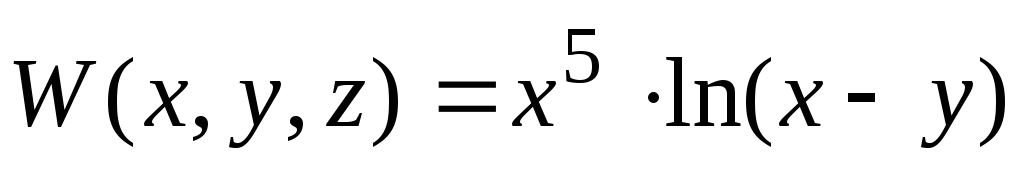 :
:
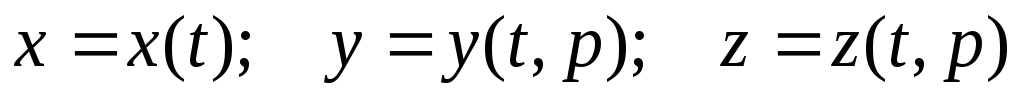 .
Найти
.
Найти
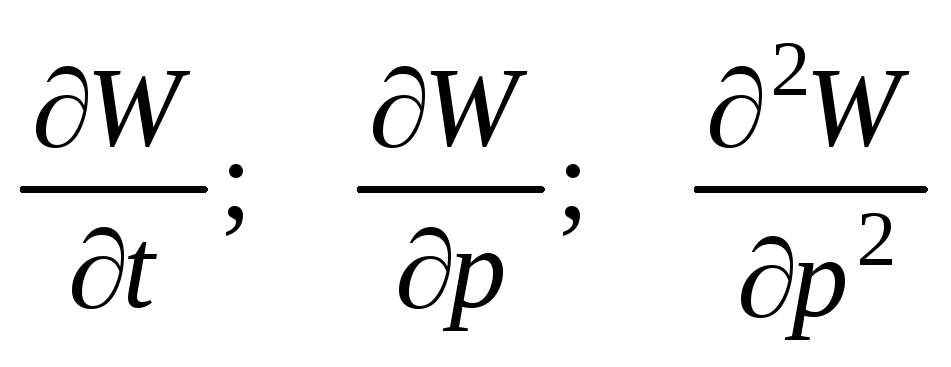 и т.п.
и т.п. -
Написать уравнение касательной плоскости и нормали к поверхности
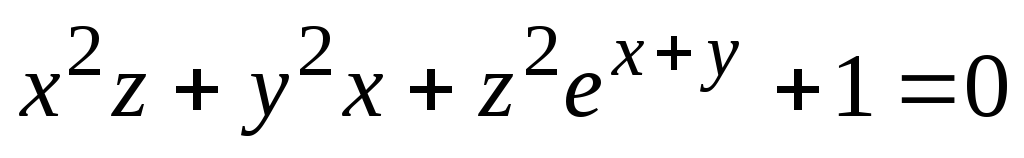 в точке
в точке
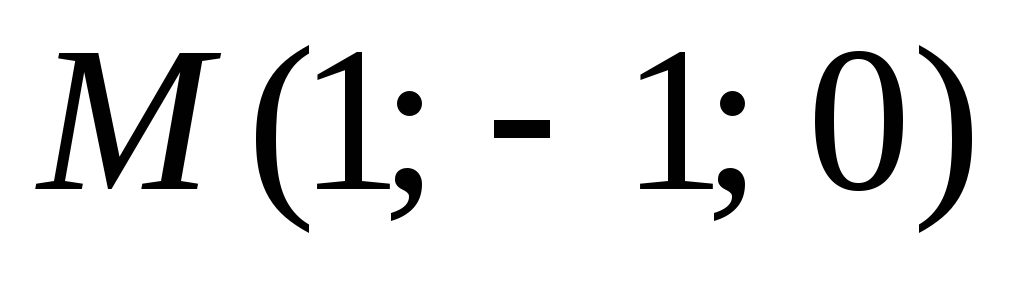 .
. -
 .
Найти
.
Найти
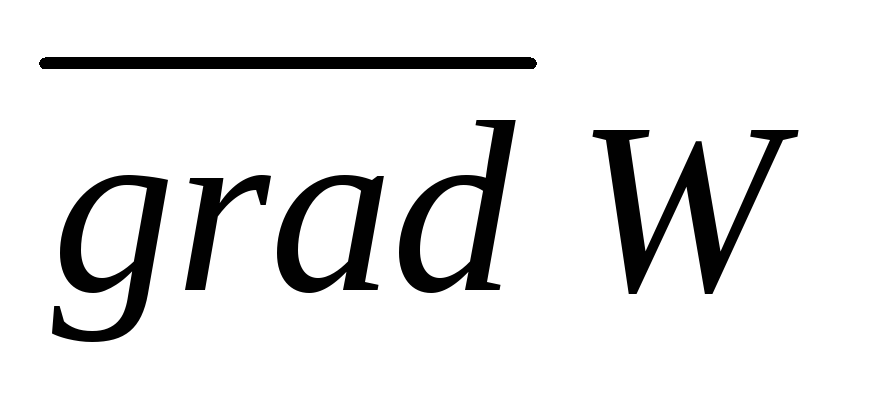 .
Найти
.
Найти
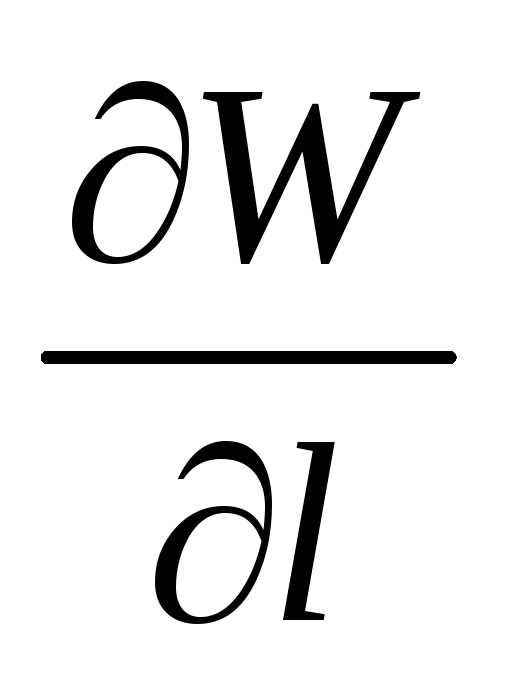 в точке
в точке
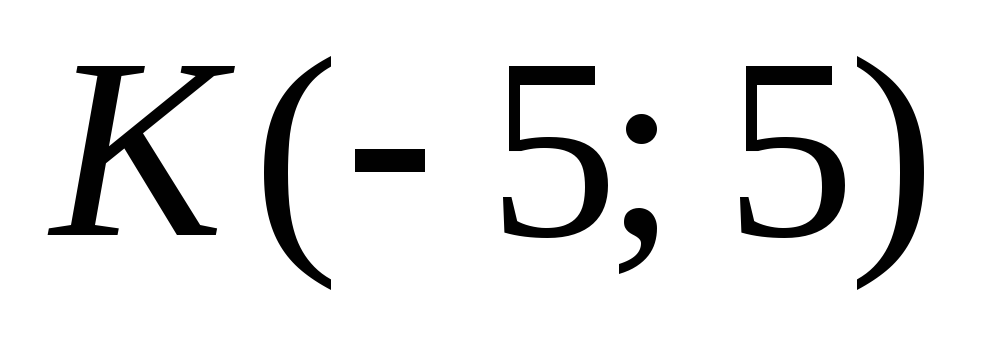 ,
если
,
если
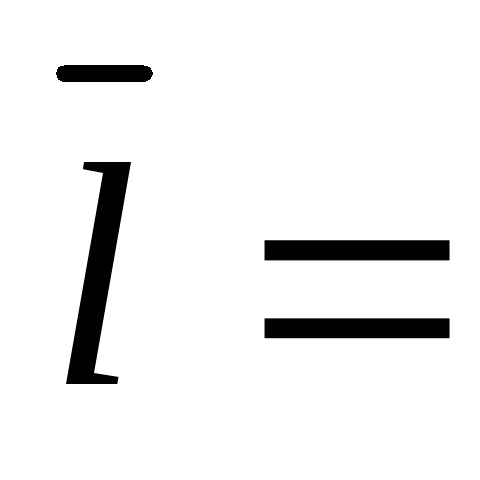
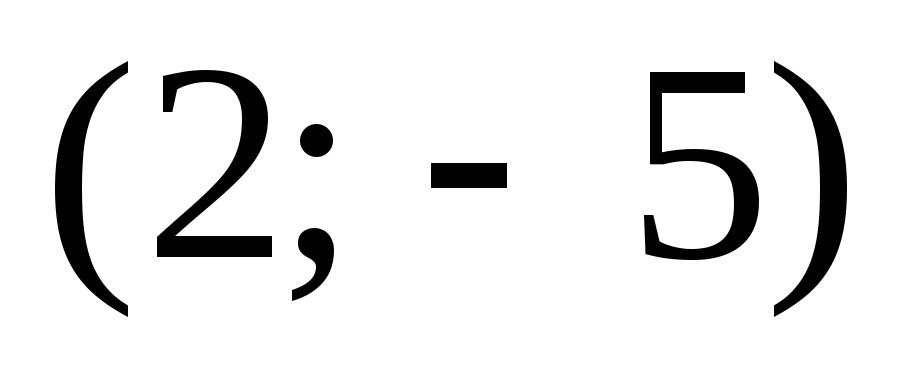 .
Изобразить
.
Изобразить
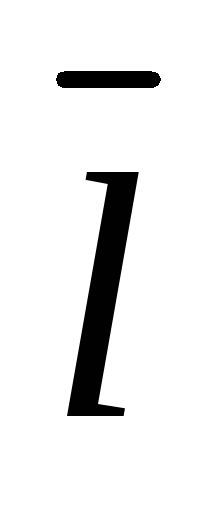 и
и
 на плоскости.
на плоскости. -
Найти экстремумы функции
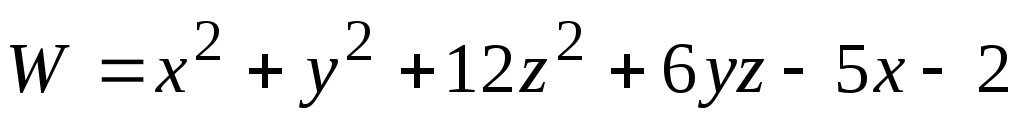 .
. -
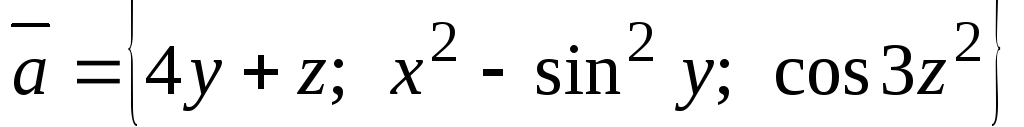 .
Найти
.
Найти
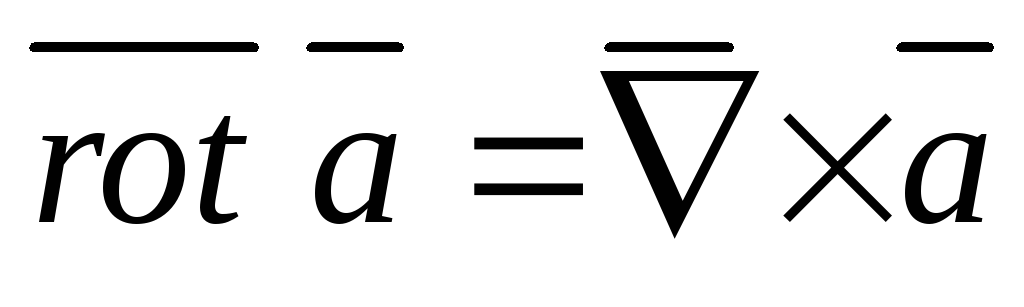 ,
,
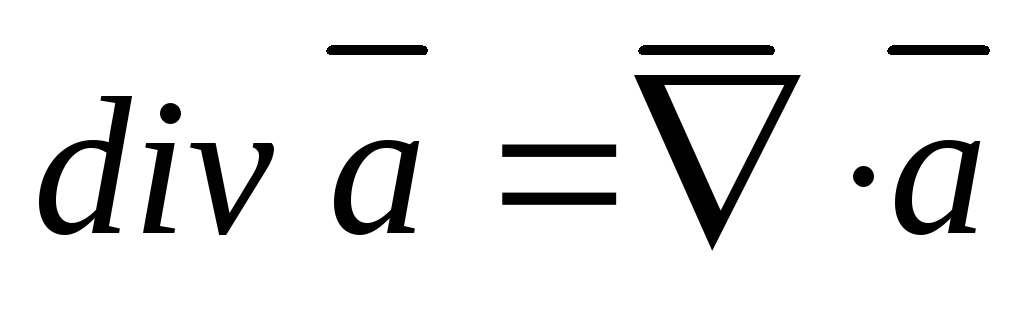 .
.
