Матан / Первый блок вопросов.Линейная алгебра

Раздел первый. Линейная алгебра.

1. Матрицы. Типы матриц. Действия с матрицами.

2. Определитель квадратной матрицы. Свойства определителя.

3. Схема Гаусса вычисления определителя.

4. Ранг матрицы. Эквивалентные преобразования. Теорема о сохранении ранга матриц при эквивалентных преобразованиях.

5. Приведение матрицы к ступенчатому виду. Ранг ступенчатой матрицы.

6. Обратная матрица. Решение матричных уравнений с помощью обратной матрицы.

7. Системы линейных уравнений (СЛУ). Решение СЛУ. Совместные, несовместные, определённые, неопределённые СЛУ. Матричная запись СЛУ. Теорема Кронеккера-Капелли. Степень свободы СЛУ.

8. Формулы Крамера для определённых СЛУ (материал в лекциях отсутствует).

9. Равносильные СЛУ. Схема Гаусса решения СЛУ. Построение ответов в неопределённых СЛУ, приведенных к ступенчатому виду (на примерах).

10. Линейные пространства. Линейные операции над элементами пространства. Линейная зависимость и независимость элементов пространства.

11. Собственные числа и собственные вектора матрицы.

12. Базис. Разложение элемента пространства по базису. Размерность пространства.

13. Ортонормированный базис. Ортогональные матрицы и их свойства.

14. Переход к новому базису. Матрица перехода.

15. Оператор в линейном пространстве. Линейный оператор. Матрица линейного оператора. Матрица линейного оператора в новом базисе.

16. Матрица линейного оператора в базисе собственных векторов.

17. Свойства собственных чисел и собственных векторов симметричной матрицы.

18. Квадратичные формы. Знакоопределённость квадратичных форм. Матричная запись квадратичных форм.

19. Приведение квадратичных форм к каноническому виду.

Стандартные примеры:

1. ; . Найти: , , .

2. Вычислить определители матриц , , , найти .

3. Решить СЛУ по формулам Крамера, по схеме Гаусса и с помощью обратной матрицы:

4. Записать ответы в СЛУ, матрицы которых уже приведены к ступенчатому виду, указать степень свободы каждой системы:

5. Найти ранги матриц. Определить, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.

;

6. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.

1) 2)

3) 4)

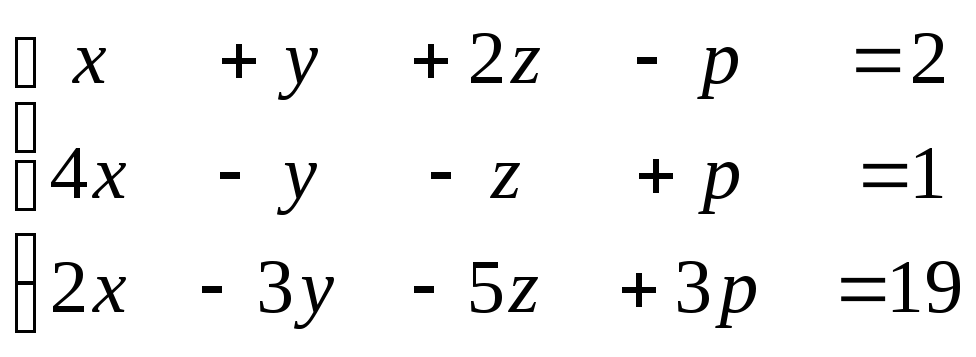
7. Найти собственные числа и собственные вектора матриц:

, , , .

Образуют ли собственные вектора матрицы базис в ? Образуют ли собственные вектора матриц , , базисы в ?

8. Показать, что вектора и образуют базис. Найти матрицу перехода к этому базису. Разложить вектора , , по этому базису.

9. Матрица линейного оператора в старом стандартном базисе имеет вид: . Найти матрицы этого оператора в базисе , и в базисе собственных векторов.

10. Привести квадратичные формы к каноническому виду. Указать тип каждой квадратичной формы и преобразование координат, приводящее квадратичную форму к каноническому виду. На рисунке показать расположение новых осей координат относительно старых.

Литература:

"Сборник задач по высшей математике" под ред. Ефимова, Демидовича. Том I, гл. 4

"Общий курс высшей математики для экономистов" под ред. Ермакова В.И., 2000г.