|
1 − x |
2 |
|
1 − x |
2 |
′ |
x dx = |
1 |
(1 |
− x |
2 |
|
− |
1 |
|
(− 2x) dx , получим |
||||
2 |
|
|||||||||||||||||||
d |
|
|
= |
|
|
2 |
|
) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy = 2 cos x (−sin x) |
1 − x2 dx +cos2 x |
|
1 |
|
(−2x)dx = |
||||||||||||||
|
2 1−x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
= 2 cos x (−sin x) |
1 − x2 |
+ cos2 x |
|
|
|
(− 2x) |
dx . |
||||||||||||
|
|
|
|
1−x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
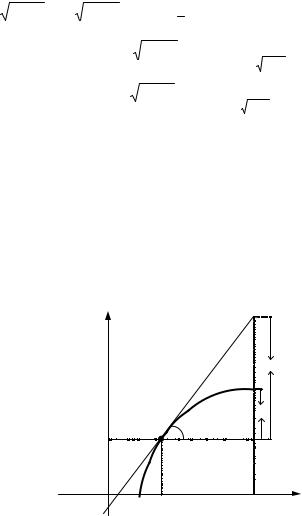
Геометрический смысл дифференциала
Геометрически дифференциал равен приращению ординаты касательной, проведенной к графику функции в точке дифференцируемости.
Доказательство
Пусть AB – касательная, проведенная к графику функции в точке x0 . По формуле
дифференциала dy = f ′(x0 ) |
x . Так как |
|
f ′(x0 )= tg α, то dy = tg α x . Из треугольника |
|
ABK (рис.1), видно, что tg α |
x = BK , где катет BK является приращением ординаты |
|||
касательной к графику функции. Следовательно, dy = BK . |
||||
|
y |
|
|
B |
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
y |
|
A |
|
α |
|
|
|
|
x |
K |
|
x0 |
|
x0 + x x |
|
|
|
Рис.1 |
|
|
Инвариантность формулы дифференциала |
||||
Теорема 1 |
|
|
|
|
Формула для дифференциала dy = f |
′ |
обладает свойством инвариантности, |
||
|
(x) dx |
|||
то есть сохраняет свой вид и в том случае, если x не простая переменная, а некоторая функция.
Доказательство
Было доказано, что для дифференциала справедлива формула dy = |
′ |
f (x) dx , если |
|
x - простая переменная. |
|
Пусть теперь x является функцией другой переменной t . То есть x = x(t), где t - простая переменная. Тогда функция y = f (x) является сложной функцией простой
переменной t : y = y(x(t)). По формуле для дифференциала dy = [y(x(t))]′t dt .
По правилу дифференцирования сложной функции
|
[y(x(t))]′t = y′x xt′, |
а так как |
xt′ dt = dx , то дифференциал dy можно записать в виде |
dy = y′x dx = |
f ′(x) dx , то есть формула дифференциала сохраняет свой вид. |
|
7 |