Вариант 30
1 |
1− 1−x2 |
2 |
2−x |
1. ∫dx |
∫ f (x, y)dy + ∫dx ∫ f (x, y)dy . |
||
0 |
0 |
1 |
0 |
2. S : z = x2 |
+ y2 ; |
S |
2 |
: z = 0 ; |
S |
3 |
: x = 0 ; |
S |
4 |
: x + y = 2 ; |
1 |
|
|
|
|
|
|
|
S5 : y = 0 .
3. S : z = 1 − x2 |
− y2 ; S |
2 |
: z = 0; S |
3 |
: y = x; S |
4 |
: y = 3x . |
1 |
|
|
|
|
4.S1 : y = 4 − z2 − x2 , S2 : y = 3 .
5.Найти координаты центра тяжести первого витка однородной
x = 4cost
винтовой линии y = 4sin t .
z = 2t
6.Найти массу части поверхности x2 + y2 + z2 = 4 , лежащей в
первом октанте, если плотность в каждой точке равна абсциссе этой точки.
7. U (x, y, z)= xy − |
x |
, M (− 4, 3,−1), l вектор |
|
|
|
MN . |
|||||
z |
|||||
|
|
|
|
||
N(1, 6, − 2). |
|
|
|
||
8.ar = −xi + yj , L : x2 + y42 =1, (x ≥ 0), от точки M (0; 2) до
точки N(0; − 2).
9. |
ar = z i − 4 y j + 2xk , S : x2 + y2 +3 = z , P : z = 4 . |
||||||||
|
r |
|
|
2 |
+ y |
2 |
)−1 |
= z |
|
10. |
= xz i − j + yk |
5(x |
|
|
. |
||||
a |
по контуру Γ: |
|
|
|
|
|
|||
|
|
|
|
|
z = 4 |
|
|
||
|
|
|
|
|
|
|
|||
r |
|
1 r |
|
|
x |
|
1 |
r |
|
y |
r |
||||
11. a |
= |
|
i |
+ |
− |
|
|
+ |
|
|
j |
− |
|
|
k . |
|
|
2 |
|
|
2 |
||||||||||
|
|
y |
|
|
|
y |
|
z |
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
84
ПРИЛОЖЕНИЕ
Полярная система координат
Полярные координаты точки M (ρ,ϕ) (рис. 25):
ρ, (ρ ≥ 0) - полярный радиус, расстояние от начала координат до точки M ;
ϕ, (0 ≤ ϕ ≤ 2π) - полярный угол, угол поворота оси Ox до
вектора OM ,
y
y M
ρ
ϕx
Оx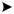 
Рис. 25.
Декартовы координаты выражаются через полярные координаты
по формулам: |
x = ρ cosφ |
. Полярный радиус выражается через |
|
|
|||
|
y = ρ sin φ |
|
|
декартовы координаты по формуле: ρ = |
x2 + y2 . |
||
Уравнение окружности x2 |
+ y2 = R2 |
имеет вид: ρ = R . |
|
Элемент |
площади dS |
в полярных координатах равен: |
|
dS = ρdρdϕ. |
|
|
|
Эллиптические координаты
Декартовы координаты |
выражаются через эллиптические |
x = aρcos ϕ |
|
координаты по формулам: |
, где ρ - полярный радиус, |
y = bρsin ϕ
ϕ - полярный угол.
85
Уравнение эллипса |
x2 |
+ |
y2 |
=1 в эллиптических координатах |
|
a2 |
b2 |
||||
|
|
|
|||
имеет вид ρ =1 . Элемент |
площади dS в эллиптических |
||||
координатах равен: dS = abρdρdϕ.
Сферическая система координат
Сферические координаты точки M (r, φ, θ) (рис. 26),
r- сферический радиус, расстояние от начала координат до точки M ;
φ- полярный угол, угол поворота оси Ox до вектора OM1 , а
точка M1 - проекция точки M в плоскость xOy ;
θ - азимутальный угол, угол поворота оси Oz до вектора
OM .
z
z
O
x φ
y
x
M
θ
r
y
y
rsinθ 
M1
Рис. 26.
Декартовы координаты выражаются через сферические координаты по формулам:
x = r cos φsin θ
y = r sin φsin θ
.
z = r cos θ
Уравнение сферы x2 + y2 + z 2 = R2 в сферических координатах имеет вид: r = R .
86