
- •РАБОЧАЯ ТЕТРАДЬ ПО ТЕМАМ 6.1, 6.2
- •Тема 6.1. Интегрирование функций нескольких переменных
- •Двойной интеграл
- •Задача 1.1
- •Задача 1.2
- •Справочный материал
- •Решение задачи 1.1
- •Решение задачи 1.2
- •Задача 2.1
- •Задача 2.2
- •Справочный материал
- •Механический смысл двойного интеграла
- •Геометрический смысл двойного интеграла
- •Решение задачи 2.1
- •Решение задачи 2.2
- •Тройной интеграл
- •Задача 3.1
- •Задача 3.2
- •Задача 3.3
- •Справочный материал
- •Решение задачи 3.1
- •Решение задачи 3.2
- •Тройной интеграл в сферических координатах
- •Решение задачи 3.3
- •Задача 4.1
- •Задача 4.2
- •Задача 4.3
- •Справочный материал
- •Решение задачи 4.1
- •Решение задачи 4.2
- •Решение задачи 4.3.
- •Задача 5.1
- •Задача 5.2
- •Задача 5.3
- •Справочный материал
- •Решение задачи 5.1
- •Решение задачи 5.2
- •Решение задачи 5.3
- •Задача 6.1
- •Задача 6.2
- •Задача 6.3
- •Справочный материал
- •Решение задачи 6.1
- •Решение задачи 6.2
- •Решение задачи 6.3
- •Тема 6.2. Теория поля
- •Скалярное поле
- •Задача 7.1
- •Задача 7.2
- •Задача 7.3
- •Справочный материал
- •Решение задачи 7.1
- •Решение задачи 7.2
- •Решение задачи 7.3
- •Векторное поле
- •Задача 8.1
- •Задача 8.2
- •Справочный материал
- •Решение задачи 8.1
- •Решение задачи 8.2
- •Задача 9.1
- •Задача 9.2
- •Справочный материал
- •Решение задачи 9.1
- •Решение задачи 9.2
- •Задача 10
- •Справочный материал
- •Теорема Стокса
- •Решение задачи 10
- •Задача 11
- •Справочный материал
- •Решение задачи 11
- •Задания к типовым расчетам
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •ПРИЛОЖЕНИЕ
- •Полярная система координат
- •Эллиптические координаты
- •Сферическая система координат
- •Обобщенно эллиптические координаты
- •Механические приложения интегралов функций нескольких переменных
- •Механические приложения двойных интегралов
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения тройного интеграла
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения криволинейного интеграла первого рода
- •Статические моменты дуги
- •Координаты центра тяжести дуги
- •Моменты инерции дуги
- •Механические приложения поверхностного интеграла первого рода
- •Статические моменты участка поверхности
- •Моменты инерции участка поверхности
(ar, grad F )= 2x3 + 2 y3 + z = 2x3 + 2 y3 + x2 + y2
и выбирая знак плюс перед интегралом, для потока P2 получим формулу:
|
|
|
|
|
P = |
∫∫ |
|
(2x3 + 2 y3 + x2 + y2 )dxdy . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В записанном двойном интеграле перейдем к полярным |
|||||||||||||||||||||||||||||||||||||||||
координатам. |
|
|
|
|
(2ρ3 (cos3 ϕ+sin3 ϕ)+ρ2 )ρdρdϕ = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
P |
= |
∫∫ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2π |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
= 2 ∫ |
|
(cos3 ϕ+sin3 ϕ)dϕ∫ρ4dρ+ ∫ |
dϕ∫ρ3dρ = |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2π |
(1 −sin2 ϕ)d |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||
= 2 |
∫ |
|
(sin ϕ) |
|
ρ4dρ−2 |
∫ |
(1 −cos2 ϕ)d |
(cosϕ) ρ4dρ+ |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ∫ |
dϕ∫ρ3dρ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
3 |
|
|
|
2π |
|
ρ |
5 |
|
1 |
|
|
|
|
|
|
|
|
cos |
3 |
|
|
|
2π |
|
ρ |
5 |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= |
|
|
|
ϕ |
|
|
|
|
− |
2 |
|
cos κ − |
|
|
ϕ |
|
|
|
|
+ |
|||||||||||||||||||||
2 sin ϕ− |
|
|
3 |
|
|
|
0 |
|
5 |
|
0 |
|
|
3 |
|
|
|
|
0 |
5 |
|
0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2π |
ρ4 |
|
|
1 |
= |
2 |
0 |
1 |
− |
2 0 |
1 |
+ |
π |
= |
π |
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
0 |
5 |
5 |
2 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение задачи 9.2
1. По теореме Гаусса – Остроградского
P = ∫∫∫div ardxdydz .
V
Так как div a =1 +1 + xy = 2 + xy , то P = ∫∫∫(2 + xy)dxdydz .
V
Область V показана на рис. 21. Она проектируется в координатную плоскость xOz на область D - круг радиуса 3.
45

Следовательно, тройной интеграл можно свести к двойному интегралу по области D .
z |
|
|
nr2 |
nr4 |
r |
|
|
n1 |
D |
|
y |
x |
nr3 |
|
|
|
|
|
Рис. 21. |
|
|
3 |
|
|
|
|
y2 |
|
|
3 |
|
|
|
9 |
|
|
|
|
|
|
|
|
||||||||
P = ∫∫dxdz∫ |
(2 |
+ xy)dy = ∫∫dxdz |
2 y + x |
|
|
|
0 |
= ∫∫ 6 |
+ |
2 |
x dxdz . |
|||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
D |
0 |
|
D |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Перейдём в этом двойном интеграле к полярным координатам:
x = ρsin ϕ |
, dxdz =ρdρdϕ (рис. 22). |
по формулам |
|
z = ρcosϕ |
|
x
3
D
3 z
Рис. 22.
Расставив пределы интеграции, запишем его в виде повторного интеграла.
2π |
3 |
|
|
9 |
|
2π |
|
|
|
ρ |
2 |
|
9 |
|
ρ |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||
P = ∫ |
dϕ∫ |
+ |
∫ |
dϕ |
|
|
|
+ |
sin ϕ |
|
|
|
|
= |
||||||
ρ 6 |
2 |
ρsin ϕ dρ = |
6 |
2 |
2 |
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
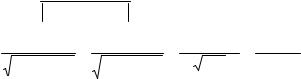
2π |
27 |
|
|
|
3 |
|
|
2π |
|
||
|
|
|
|||||||||
= 3 ∫ |
9 + |
|
sin ϕ dϕ = 27 |
ϕ− |
|
cosϕ |
|
= 27 |
2π = 54π. |
||
2 |
2 |
||||||||||
0 |
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|||
2. Теперь вычислим поток, разбивая его на три потока |
|||||||||||
|
|
|
|
P = P1 + P2 + P3 , |
|
|
|
||||
где P1 |
- проток через поверхность цилиндра, а P2 и P3 - потоки |
||||||||||
через плоскости |
y = 0 и |
y = 3 соответственно. |
|
||||||||
P1 = ∫∫(ar, nr1 )dσ ,
σ1
где nr1 - единичная нормаль, которую можно определить через градиент по формуле
nr1 = grad F ((x, y, z)) , F (x, y, z)= x2 + z2 . grad F x, y, z
nr1 = 2xi +2zk = 2xi +2zk |
= |
2xi +2zk |
= xi + zk . |
|||
4x2 +4z2 |
4(x2 + z2 ) |
|
4 9 |
3 |
||
r |
r |
x2 + xyz2 |
|
|
|
|
Поскольку (a, |
n )= |
|
, |
поток через поверхность |
||
|
||||||
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
цилиндра можно записать в виде поверхностного интеграла первого рода.
P = 13 ∫∫(x2 + xyz2 )dσ.
σ1
Интегрирование ведется по цилиндрической поверхности σ1 ,
заданной уравнением x2 + z2 = 9 . Если задать поверхность σ1 параметрическими уравнениями
x = 3sin ϕ, y = y , z = 3cosϕ,
то переменные ϕ и y на заданной поверхности меняются в пределах:
0 ≤ ϕ ≤ 2π, 0 ≤ y ≤ 3 .
Векторное уравнение поверхности имеет вид:
47
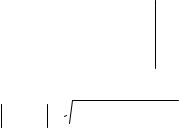
rr = 3sin ϕi + yj +3cosϕk .
Вычислив производные rrϕ′ = 3cosϕir −3sin ϕk |
и rr′ = j , |
|
y |
запишем векторное произведение |
|
[rrϕ′, rry′]= |
|
ir |
rj |
|
|||
|
3cosϕ |
0 |
|
|
|
0 |
1 |
|
|
|
|
r k
−3sin ϕ 0
3sin ϕ = 0 .3cosϕ
Модуль векторного произведения равен
[rrϕ′, rry′] =  9sin2 ϕ+9cos2 ϕ = 3 .
9sin2 ϕ+9cos2 ϕ = 3 .
Тогда поток через поверхность σ1 , учитывая замечание 2, можно записать в виде двойного интеграла
P= 13 ∫∫D (9sin2 ϕ+27sin ϕcos2 ϕ y)3dϕdy ,
вкотором областью интегрирования D является прямоугольник
0 ≤ ϕ ≤ 2π, 0 ≤ y ≤ 3 .
Расставим пределы интеграции и вычислим двойной интеграл
|
|
|
2π |
|
3 |
(9sin2 ϕ+27sin ϕcos2 ϕ y)dy = |
|
||||||||||||||||
P |
= 1 3 |
∫ |
dϕ |
∫ |
|
||||||||||||||||||
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
3 |
|
|
|
2π |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
= ∫9sin2 ϕdϕ∫ dy + ∫ 27sin ϕcos2 ϕdϕ∫ ydy = |
|
||||||||||||||||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
2π |
1 −cos 2ϕ |
dϕ y |
|
3 |
2π |
cos2 ϕd cosϕ |
y2 |
|
3 |
|
|||||||||||||
|
|
|
|||||||||||||||||||||
= 9 ∫ |
|
|
|
|
|
|
0 |
−27 ∫ |
|
|
|
0 |
= |
||||||||||
|
|
2 |
|
|
|
2 |
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
2π |
|
|
|
|
|
|
9 |
|
cos3 |
ϕ |
|
2π |
|
|
|
|
||||
= |
9 |
|
|
−cos 2ϕ)dϕ− |
27 |
|
|
. |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||
2 |
3 ∫(1 |
2 |
3 |
|
|
|
0 |
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Второе слагаемое в последней формуле равно нулю. Интеграл |
|||||||||||||||||||||||
от cos2ϕ по промежутку длины периода |
[0, 2π] |
также равен нулю. |
|||||||||||||||||||||
Поэтому
48
