
- •2. Определение амплитуды собственных колебаний и графическое изображение собственных форм
- •3. Проверка ортогональности собственных форм колебаний
- •5. Определение амплитудных значений инерционных сил
- •6. Определение эпюры изгибающих моментов от действия собственного веса вибраторов и амплитудных значений изгибающих моментов при вынужденном стационарном режиме колебания рамы
- •7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции
- •8. Определение максимального напряжения и проверка условий прочности в наиболее опасном сечении
- •5.7. Сейсмические колебания системы с конечным числом степеней свободы
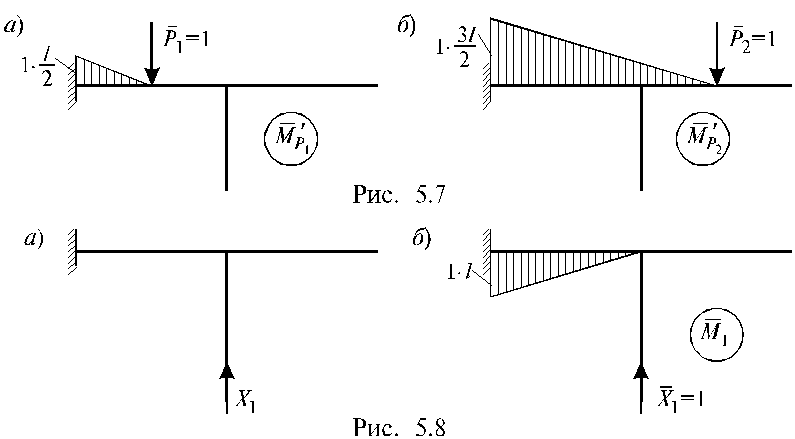
![]() и
и
![]() находим перемножением эпюр
находим перемножением эпюр
![]() и
и![]() по формуле Мора.
по формуле Мора.
Здесь
![]() определяется как результат переумножающая
эпюры
определяется как результат переумножающая
эпюры![]() (рис.5.7,
б) самой на себя,
(рис.5.7,
б) самой на себя,
![]() как
результат переумножения
как
результат переумножения
![]() (рис.5.7,
б) с
(рис.5.7,
б) с
![]() (рис.5.8,
а).
(рис.5.8,
а).
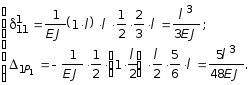 (5.45)
(5.45)
С учетом (5.45) из решения (5.44) получим:
![]() .
.
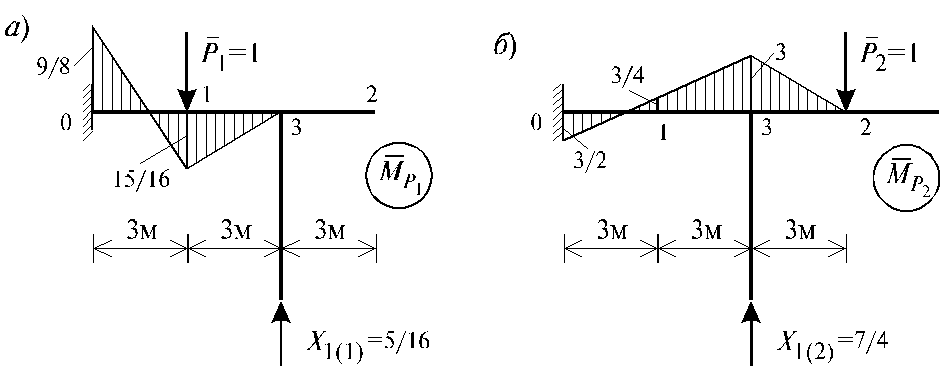
Эпюра изгибающих моментов в заданной системе от действия сил Р1 =1 и Х1 = 5/16 изображена на рис. 5.9, a.
Рассчитываем раму на действие силы Р2 = 1. Каноническое уравнение метода сил в данном случае принимает вид:
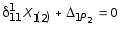 . (5.46)
. (5.46)
Здесь
![]() определяется как результат перемножения
эпюры моментов, изображенных на
рис. 5.7, б
и 5.8, б,
в соответствии с формулой Мора:
определяется как результат перемножения
эпюры моментов, изображенных на
рис. 5.7, б
и 5.8, б,
в соответствии с формулой Мора:
![]() . (5.47)
. (5.47)
С учетом
значения
![]() из (5.45) и значения
из (5.45) и значения
![]() из (5.47) и из (5.46) получим:
из (5.47) и из (5.46) получим:
![]() .
.
Эпюра изгибающих моментов от действия сил Р2 = 1 и Х1 = = 7/4 в заданной системе изображена на рис. 5.9, б.
Единичное
перемещение d11
определяется по формуле Мора в результате
перемножения эпюры
![]() самой на себя, применяя формулы умножения
двух эпюр моментов в виде двух трапеций
на произвольном участке, приведенная
в (2.8). Получим:
самой на себя, применяя формулы умножения
двух эпюр моментов в виде двух трапеций
на произвольном участке, приведенная
в (2.8). Получим:
![]()
![]() м/кН.
м/кН.
Единичное
перемещение d22
определяется по формуле Мора перемножением
эпюры
![]() самой на себя (рис. 5.9, б):
самой на себя (рис. 5.9, б):
![]()
![]() м/кН.
м/кН.
Единичное
перемещение d12
определяется по формуле Мора в результате
перемножения эпюр
![]() и
и
![]() ,
изображенных соответственно на
рис. 5.9, а, б:
,
изображенных соответственно на
рис. 5.9, а, б:
![]()
![]() м/кН.
м/кН.
Решив уравнение (5.40), получим:
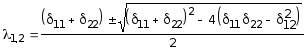 ,
,
откуда
![]() .
.
Окончательно
![]() =166.75×10-6 м/кН;
=166.75×10-6 м/кН;
![]() =10.35×10-6 м/кН.
=10.35×10-6 м/кН.
По формуле (5.41) определяется значение собственной частоты рассматриваемой рамы:
![]() c-1;
c-1;
![]() c-1.
c-1.
Периоды собственных колебаний рассматриваемой системы принимают значения: T1 = 2p/w1 = 0.116 c; T2 = 2p/w2 = 0.029 c.
2. Определение амплитуды собственных колебаний и графическое изображение собственных форм
Для
вычисления значения отношений амплитуды
собственных колебаний из (5.42), предварительно
определив m = 20/9.81 »
» 2.04 кН×с2/м,
имеем при
![]() = 1
и при
= 1
и при
![]() =
1, соответственно:
=
1, соответственно:
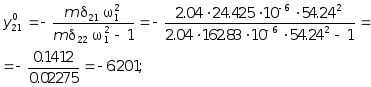

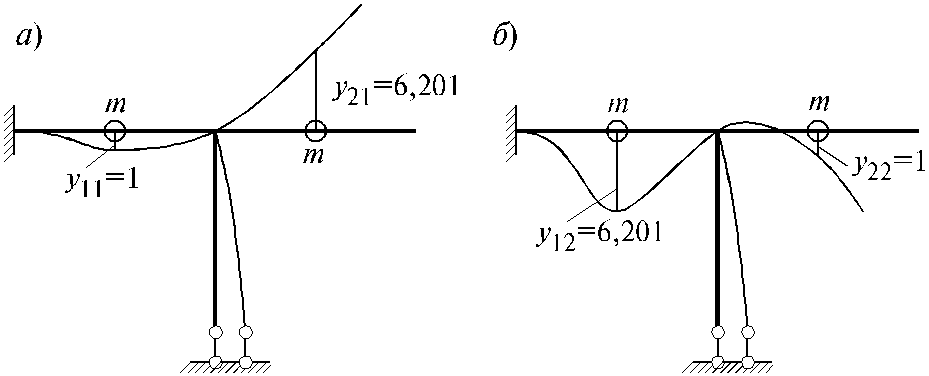
Формы собственных колебаний рассматриваемой системы изображены на рис. 5.10 (а - первая форма; б - вторая форма).
3. Проверка ортогональности собственных форм колебаний
Из условия ортогональности (5.43) имеем:
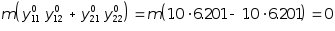 .
.
Рис. 5.10
В стационарном режиме круговая частота вынужденных колебаний системы имеет значение:
Q = 2pn/60 = 6.28×600/60 = 62.8 c-1.
Сопоставим величину Q с величиной ближайшей собственной частоты рамы w1:
![]() 100% = 4.94 < 30%.
100% = 4.94 < 30%.
Во избежание резонансных колебаний надо изменить величину w1 или Q. В данном случае, принимая n = 900 об/мин, получим:
Q = 2pn/60 = 6.28×900/60 = 94.2 c-1;
![]() 100% = 35.52 > 30%.
100% = 35.52 > 30%.
Рис. 5.11

Примерный вид графика коэффициента динамичности в зависимости от Q/w1. изображен на рис.5. 11.
5. Определение амплитудных значений инерционных сил
В соответствии с принятым обозначением по формулам (5.34) и (5.35) последовательно определяем:
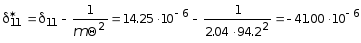 м/кН;
м/кН;
 м/кН;
м/кН;
![]() кН;
кН;
 м/кН;
м/кН;
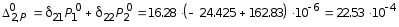 м/кН;
м/кН;
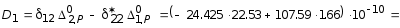
![]() м2/кН;
м2/кН;
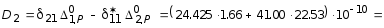
![]() м2/кН;
м2/кН;
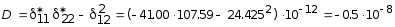 м2/кН.
м2/кН.
По (5.33) определяем амплитудные значения инерционных сил:
![]() =
|D1/D
|=
|3.72/0.5| =
7.44 кН;
=
|D1/D
|=
|3.72/0.5| =
7.44 кН;
![]() =
|D2/D
|=
|9.64/0.5 |=
19.28 кН.
=
|D2/D
|=
|9.64/0.5 |=
19.28 кН.
6. Определение эпюры изгибающих моментов от действия собственного веса вибраторов и амплитудных значений изгибающих моментов при вынужденном стационарном режиме колебания рамы
Значение изгибающих моментов, возникающих от действия собственного веса вибраторов, в произвольном сечении определяется по формуле:
![]() .
.
Определяем значение
![]() в характерных сечениях (0; 1; 2; 3) рамы (см.
рис. 5.9):
в характерных сечениях (0; 1; 2; 3) рамы (см.
рис. 5.9):
сечение
0:
![]() = 20×(9/8 - 3/2)
= -7.5 кН×м;
= 20×(9/8 - 3/2)
= -7.5 кН×м;
сечение
1:
![]() =
20×(-15/16 + 3/4)
= -3.75 кН×м;
=
20×(-15/16 + 3/4)
= -3.75 кН×м;
сечение
2:
![]() =
0;
=
0;
сечение
3:
![]() =
20×(0 +
3) = 60 кН×м.
=
20×(0 +
3) = 60 кН×м.
Эпюра изгибающих моментов
![]() приведена на рис. 5.12.
приведена на рис. 5.12.
Амплитудные значения изгибающих моментов от действия внешних динамических и инерционных нагрузок в соответствии с (5.37) определяются:
![]() =
= ![]()
![]()
![]() .
.
Рис. 5.12
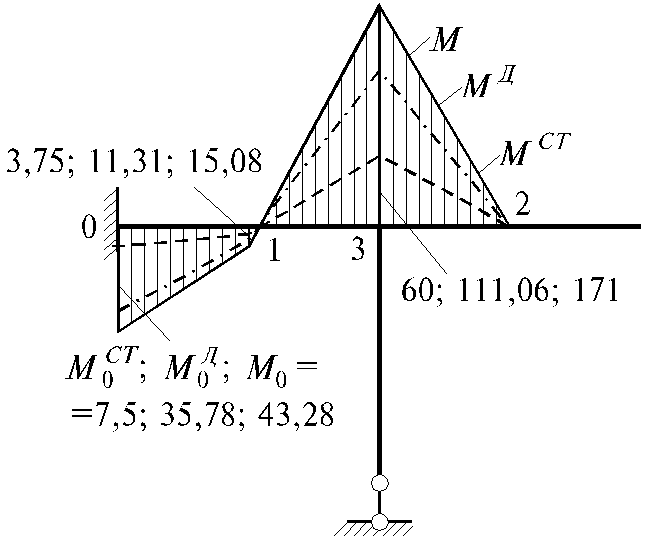
![]() в характерных сечениях имеет
в характерных сечениях имеет
следующие значения:
сечение 0: ![]() кН×м;
кН×м;
сечение 1: ![]() кН×м;
кН×м;
сечение 2:
![]() =
0;
=
0;
сечение 3: ![]() кН×м.
кН×м.
Эпюра
![]() изображена на рис. 5.12 (пунктиром).
изображена на рис. 5.12 (пунктиром).
7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции
Результирующее значение изгибающих моментов, действующих в характерных сечениях при одновременном действии статических и динамических нагрузок, определяется по формуле:
Mk
=
![]() +
+![]() .
.
Эпюра
Mk,
как и эпюры
![]() и
и
![]() ,
изображены на рис. 5.12.
,
изображены на рис. 5.12.
Из рис. 5.12 согласно эпюре М следует, что наиболее опасным является сечение 3.
