20.3. Пример расчета балки в виде системы с одной степенью свободы

Проверить прочность балки в рабочем режиме вибратора, расположенного по середине пролета балки (рис.20.2, а), учитывая только вертикальную составляющую вертикальной силы: , принимая:G = 15 кН - вес вибратора; Р₀ = P_a = 3 кН - вес не­уравновешенных частей вибра­тора; e = 0,01 м - эксцентриситет относительно оси вращения неуравновешенных частей; = 30 с^-1 - круговая частота внешней силы; l = 4 м - пролет балки. Поперечное сечение балки выполнено из двутавра №20, материал Ст3. Следовательно, Е=2,1×10⁸ кН/м² - модуль деформации материалов; J_x =1,84×10^-5 м⁴ - момент инер­ции; W_x = 1,84×10^-4 м³ - момент сопротивления поперечного сечения; R = 25×10⁴ кН/м² - расчетное сопротивление; = 0,1- логарифмический декремент. Интенсивность распределенных нагрузок принимается равной: q = 4 кН/м.

На первом этапе для выполнения расчетов необходимо определить величину коэффициента динамичности. Для этого сначала определим величину коэффициента затухания .

Воспользуемся эпюрой моментов, изображенной на рис.20.2, б и по формуле Мора определим :

.

Круговая частота собственных колебаний без учета затуханий:

c^-1.

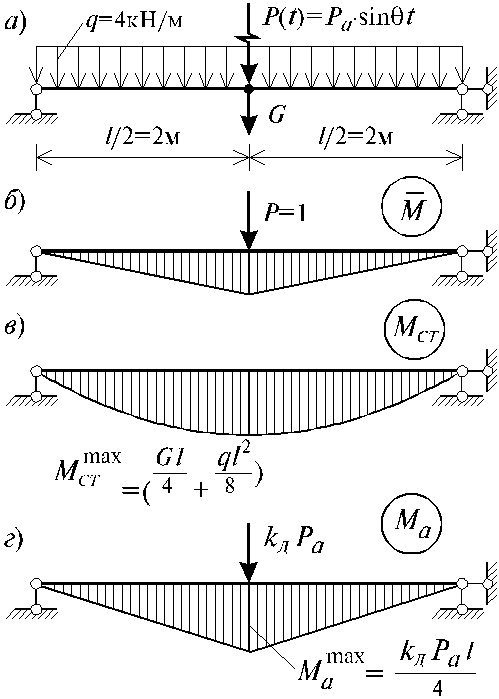
Рис.20.2

Собственная частота системы с учетом затухания колебания принимает значения:

c^-1.

Коэффициент динамичности определяется из (14.10) по формуле:

.

Последовательно определим максимальное значение момента в опасном сечении (рис.20.2, в, г) от статических и динамических сил:

кН×м;

кН×м.

Максимальное напряжение в опасном сечении принимает значение:

кН/м²,

т.е. прочность конструкций обеспечена.

20.4. Свободные колебания системы с произвольнымчислом степеней свободы

Рассмотрим свободные колебания системы с конечным числом степеней свободы. В качестве объекта рассмотрим упругую невесо­мую балку, изображенную на рис.14.3 и с n сосредоточенными мас­сами m₁, m₂, m₃,..., m_n. Пренебрегаем продольными деформация­ми оси балки в процессе колебаний. При этом положение системы однозначно определяется перемещениями сосредоточенных масс y_i (t) (i = 1,2,3,...,n) в произвольные моменты времени t, вызван­ными упругими деформациями балки в поперечном направлении.

Рис.14.3

Во время движения, пренебрегая сопротивлением внутренних и внешних сил, на балку будут действовать в качестве внешних сил инерционные силы , (i = 1,2,3,...,n). Применяя метод сил, перемещение произвольной массы y_i (t) записывается в виде суммы:

, (14.11)

где - перемещение i-ой массы от статической единичной силы, приложенной к k-ой массе от статической единичной силы по направлению соответствующей инерционной силы.

Подставляя выражение инерционных сил в систему уравнений (14.11), получим:

, (i = 1,2,3,...,n). (14.12)

Система дифференциальных уравнений движения (14.12), опи­сывающая свободные колебания заданной балки, представляет со­бой замкнутую систему дифференциальных уравнений второго по­рядка с постоянными коэффициентами, решение которой в общем случае записывается в виде:

. (14.13)

Рассмотрим одно частное произвольное решение соответствую­щее r-ой форме колебаний:

. (14.14)

Подставляя (14.14) в (14.12) получим:

, (14.15)

которое распадается на две группы уравнений:

(14.16)

и

(14.17)

Решение уравнения (14.16) записывается в виде:

, (r = 1,2,3,...,n). (14.18)

Как видно из (14.18), по произвольной форме r = 1,2,3,...,n коле­бания происходят по гармоническому закону с частотой . Здесь  - частота собственных колебаний заданной системы, соответст­вующая r-ой форме.

Согласно (14.14) - является перемещением i-ой массы при r-ой форме колебания, значения которой определяется из решения системы алгебраических уравнений (14.17).

Система (14.17) относительно (i = 1,2,3,...,n) имеет различ­ные решения. Очевидно, решение º 0 свидетельствует об отсут­ствии движения системы, т.е. состояние покоя системы, которое нас не интересует.

Система (14.17) может иметь решения, отличные от нулевого лишь в том случае, когда ее определитель равен нулю, т.е. когда выполняется условие:

, (14.19)

где принято обозначение .

Раскрывая определитель (14.19), получаем уравнения n-ой степени относительно , а при его решении получим n значений  . Каждому значению (r = 1,2,3,...,n) будет соответствовать своя собственная частота:

,

и свой собственный вектор:

.

При этом собственные формы упругих систем ортогональны между собой:

, (r,k = 1,2,3,...,n;    r ¹ k). (14.20)

Величины непосредственно из решения (14.17) определить нельзя, они могут быть найдены с точностью до произвольного постоянного множителя, т.е. по существу могут быть найдены от­ношения между . Принимая обозначения система (14.17) преобразуется в вид:

Последняя система имеет одно лишнее уравнение, так как име­ем n уравнений относительно (n-1) неизвестных . Отбрасывая одно из этих уравнений, решая оставшуюся систему определяют все неизвестные.

Далее, полагая _, по формуле определяются все остальные амплитуды перемещений масс приr-ой произволь­ной форме колебаний.

Возвращаясь к выражению (14.13) с учетом (14.18) можем запи­сать:

(14.21)

Учитывая, что ,A_r и B_r являются произвольными постоян­ными, решение (14.21) можно записать в более удобной форме:

и можно выразить через начальные условия каждой массы приt = 0, которыми являются перемещения i-ой массы и ее скорости, и следовательно, задача о свободных колеба­ниях системы с произвольным числом свободы будет полностью решена.