3. Проверка нормальности распределения выходной величины

При рассмотрении большинства статистических процедур предполагалось, что выходная величина подчиняется нормальному закону распределения. Это предположение можно проверить разными способами. Наиболее строгим из них является применение критерия χ² Пирсона. Для этого необходимо иметь выборку достаточно большого объёма: N > 50 – 150 (в нашем случае 60). Диапазон изменения выходной величины в этой выборке разбивается на интервалы. Подсчитывают количество наблюдений т_i, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый i-й интервал. Для этого используют формулу:

P_i = Ф(z₂) – Ф(z₁), (3.1)

где

z₁ = (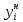–)/S, (3.2)

z₂ = (–)/S , (3.3)

где – среднее арифметическое выборки;

S – среднеквадратическое отклонение выборки;

– нижняя граница i-го интервала;

– верхняя граница i-го интервала;

Ф(z) – нормированная и центрированная функция распределения для нормального закона:

(3.4)

Следующим этапом является вычисление величины χ² _расч по формуле:

χ²_расч =, (3.5)

где     n – количество интервалов. По выбранному уровню значимости q и числу степеней свободы f = n – 3 из табл. 4 приложения отыскивают χ² _табл. Гипотезу о нормальности распределения на данном уровне значимости можно принять, если χ² _расч < χ² _табл.

В табл. 3.1 представлены результаты предварительной серии опытов в соответствии с заданием.

Таблица 3.1

448,317	438,751	487,962
434,272	454,086	482,270
474,572	423,699	460,883
495,419	442,096	427,474
518,044	538,144	495,337
460,358	386,081	499,496
469,971	467,355	490,550
415,412	526,637	524,131
495,974	442,740	420,313
498,931	449,031	427,199
499,024	401,111	422,723
427,832	394,171	551,865
452,708	469,612	467,394
419,010	443,508	488,295
495,889	474,113	475,336
550,870	484,477	494,059
474,956	440,454	478,138
478,867	485,239	522,954
506,936	439,084	454,519
406,981	495,716	473,325

Далее приводится процедура проверки нормальности распределения выходной величины по пунктам.

3.1. Сортируем значения случайной величины Y в порядке возрастания.

3.2. Задаемся количеством интервалов: n = 10.

3.3. Определяем длину интервала:

h =, (3.6)

h =.

где     y_max, y_min– округлённые до первых цифр после запятой соответственно в большую и меньшую сторону максимальное и минимальное значения случайных величин выборки (551,865 и 386,081).

3.4. Определяем границы интервалов:

, i = 1…10; (3.7)

, i = 1…10. (3.8)

Данные заносим в табл. 3.2.

3.5. Вычисляем середины интервалов:

, (3.9)

в частности, для первого: = 394,295.

Для остальных интервалов процедура нахождения y_i^c аналогичная. Данные заносим в табл. 3.2.

3.6. Выбираем значения случайной величины Y, попадающие вi-й интервал и заносим в табл. 3.2.

3.7. Считаем количество значений случайной величины m_i, попадающих вi-й интервал, и заносим в табл. 3.2.

Таблица 3.2

№ интервала	Границы интервалов, yiн, yiв	Середина интервала, yic	Точки	Количество замеров, попавших в интервал, mi
1	386,00 – 402,59	394,295		3
2	402,59 – 419,18	410,885		3
3	419,18 – 435,77	427,475		7
4	435,77 – 452,36	444,065		8
5	452,36 – 468,95	460,655		7
6	468,95 – 485,54	477,245		12
7	485,54 – 502,13	493,835		12
8	502,13 – 518,72	510,425		2
9	518,72 – 535,31	527,015		3
10	535,31 – 551,90	543,605		3

3.8. По результатам расчётов строим гистограмму распределения случайной величины Y, которая представлена на рис. 1.

3.9. Вычисляем вспомогательные величины и заносим их в следующую таблицу.

Таблица 3.3

№ интервала	Середина интервала	Количество замеров, попавших в интервал, mi	mi·yiс	(yiс –)2	mi( yiс – )2
1	394,295	3	1182,885	5409,455	16228,366
2	410,885	3	1232,655	3244,328	9732,983
3	427,475	7	2992,325	1629,656	11407,593
4	444,065	8	3552,520	565,441	4523,527
5	460,655	7	3224,585	51,682	361,772
6	477,245	12	5726,940	88,379	1060,546
7	493,835	12	5926,020	675,532	8106,385
8	510,425	2	1020,850	1813,142	3626,283
9	527,015	3	1581,045	3501,207	10503,622
10	543,605	3	1630,815	5739,279	17219,187
Сумма	–	60	28070,640	22718,551	82770,264

3.10. Вычисляем выборочное среднее:

, (3.10)

где N – общее количество наблюдений (60);

m_i – количество наблюдений, попавших в i-й интервал;

n – количество интервалов, на которые разбита выборка (10). Тогда

467,844.

3.11. Вычисляем выборочную дисперсию:

, (3.11)

1402,886.

3.12. Вычисляем среднеквадратичное отклонение:

S = , (3.12)

S == 37,455.

3.13. Для каждого интервала по формулам (3.2) и (3.3) находим значения z₁ и z₂, в частности, для первого интервала:

z₁ = (386,000 – 467,844)/37,455 = –2,19;

z₂ = (402,590 – 467,844)/37,455 = –1,74.

Аналогично рассчитываем значения z₁ и z₂ для других интервалов, и результаты заносим в столбики 5 и 6 таблицы 3.4.

Таблица 3.4

№ интервала	yiн	yiв	mi	z1	z2	Ф(z1)	Ф(z2)	Pi	Pi·N	(mi – Pi·N)2	(mi – Pi·N)2/Pi·N
1	2	3	4	5	6	7	8	9	10	11	12
1	386,00	402,59	3	–2,19	–1,74	0,01426	0,04093	0,02667	1,600	1,9599	1,2249
2	402,59	419,18	3	–1,74	–1,30	0,04093	0,09680	0,05587	3,352	0,1241	0,0370
3	419,18	435,77	7	–1,30	–0,86	0,09680	0,19489	0,09809	5,886	1,2418	0,2110
4	435,77	452,36	8	–0,86	–0,41	0,19489	0,34090	0,14601	8,761	0,5784	0,0660
5	452,36	468,95	7	–0,41	0,03	0,34090	0,51197	0,17106	10,264	10,6525	1,0379
6	468,95	485,54	12	0,03	0,47	0,51197	0,68082	0,16886	10,131	3,4918	0,3447
7	485,54	502,13	12	0,47	0,92	0,68082	0,82121	0,14039	8,423	12,7916	1,5186
8	502,13	518,72	2	0,92	1,36	0,82121	0,91309	0,09187	5,512	12,3361	2,2379
9	518,72	535,31	3	1,36	1,80	0,91309	0,96407	0,05098	3,059	0,0035	0,0011
10	535,31	551,90	3	1,80	2,24	0,96407	0,98745	0,02338	1,403	2,5501	1,8175
												8,4966

3.14. По таблице 6 приложения, [4], находим для каждого интервала значения Ф(z₁) и Ф(z₂), учитывая, что Ф(z) для отрицательных значений имеет вид

Ф(– z) = 0,5 – Ф(z). (3.13)

Значения Ф(z₁) и Ф(z₂) можно также вычислить непосредственно по формуле (3.4), используя интегрированную систему MathCAD. Полученные данные заносим в колонки 7 и 8 таблицы 4.3.

3.15. Вычисляем теоретическую вероятность по формуле (3.1), заносим в колонку 9 таблицы 3.4.

3.16. Рассчитываем теоретическую частоту попадания опытных данных в i-й интервал (колонка 10 таблицы 3.4).

3.17. Рассчитываем колонки 11 и 12 таблицы 3.4 по соответствующим формулам в верхней строке таблицы.

3.18. Суммируя показания последнего столбца, получаем значение χ²_расч = 8,4966≈8,5.

3.19. Находим число степеней свободы:

f = n – 3 = 10 – 3 = 7.

где     n – число интервалов.

3.20. Уровень значимости q = 5 %. По табл. 5 прил., [2], или таблицам критических значений критерия Пирсона [3] находим χ²_табл = 14,07.

3.21. Поскольку χ²_расч = 8,5 < χ²_табл = 14,07, то гипотеза о нормальности распределения принимается на данном уровне значимости.