Сопромат - заочно / о проекте / Лекции / Контрольные работы / Консультации / Литература / Экзамен Лекция 9. Устойчивость сжатых стержней
Практика эксплуатации конструкций показала, что в некоторых случаях выполненных расчетов на прочность и жесткость оказалось недостаточно для обеспечения необходимой работоспособности. Так при сжатии достаточно длинных и тонких стержней вместо укорочения в соответствии с законом Гука они могут изогнуться (рис.9.1а). При прямом изгибе балок направление прогиба балки может существенно отклониться от линии действия нагрузки (рис.9.1б), и, наконец, при действии внутреннего давления на цилиндрическую оболочку ее деформации в некоторый момент перестают быть осесимметричными, оболочка искривляется и принимает некоторую новую форму (рис.9.1в).
Во всех случаях конструкция вместо
начального равновесного положения
занимала новое положение равновесия.
Это явление было названо потерей
устойчивости. Явление потери
устойчивости связано с величиной
действующей нагрузки. Если, например,
сила Р сжимающая стержень меньше
некоторой критической величины Ркр,
то стержень сохранит свое прямолинейное
положение, если больше, то стержень
иск
ривится,
потеряет устойчивость.
Рассмотрим решение задачи об устойчивости сжатого стержня. Пусть стержень, оба конца которого закреплены шарнирно, сжат силой Ркр (рис.9.2). Стержень искривился так, что в сечении z прогиб составил δ. Приближенное дифференциальное уравнение изогнутой оси балки имеет вид:
.
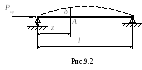
Изгибающий момент в сечении z в изогнутом состоянии равен моменту силы Ркр, но обратного направления, а, следовательно, и знака
.
Тогда дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости будет
.
Обозначая
(9.1) получим линейное дифференциальное
уравнение второго порядка относительно
прогиба δ
.
Его общее решение имеет вид
,
где С и D – постоянные интегрирования, определяемые из условий на опорах. На опорах стержня прогиб равен нулю, т.е. 1) при z=0, δ=0;
2) при z=l,
δ=0. Подставляя
первое условие в уравнение прогибов
получим С=0, из второго условия
получим
.
Последнее соотношение справедливо при
,
где n – любое целое
число.
Откуда
,
с учетом принятого ранее обозначения
(9.1), получим
.
Минимальное действительное значение критической силы получится при n=1
.
(9.2)
Это и есть формула Эйлера для критической силы.
Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной
.
Влияние способов закрепления концов стержня на критическую силу
Формула Эйлера получена для случая шарнирного закрепления концов стержня, когда потеря устойчивости происходит по одной полуволне. Для других случаев закрепления формула Эйлера принимает вид
,
(9.3)
где μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.
Значение коэффициента μ
с достаточной для расчетной практики
точностью может быть вычислено по
формуле
,
где s – количество
полуволн по которым происходит потеря
устойчивости при данном способе
закрепления концов стержня.
