modelirovanie_1 вар 7

«Математическое моделирование механической части электропривода с электродвигателем постоянного тока независимого возбуждения».

1. Цель работы.

Исследование динамических свойств механической части электропривода на примере трехмассовых и эквивалентных им двухмассовых расчетных схем.

Вариант	Параметры
№	J2 кг м2	J3 кг м2	С12 Нм	С23 Нм	12	23	MC Нм	 с-2	1 с-1
7	0,15	0,8	175	200	0,1	0,15	50	100	230

2. Выбор электродвигателя

Выбор двигателя ориентировочно выбирается по мощности:

Р_Н  k_з М_{С.М.МАКС} _М.МАКС

Р_{Нmin =} 1,2*50*230 = 13800 Вт

Р_{Нmax =} 10*50*230 = 115000 Вт

где k_з = 1,2…10 – коэффициент, учитывающий требования к динамическим характеристикам ЭП (меньшему времени переходного процесса соответствует большее значение коэффициента). При мощности до 1,5 кВт рекомендуется выбрать двигатель на номинальное напряжение U_H 110 В, от 1,5 до 6 кВт на 220 В, свыше 6 кВт – на 440 В.

Выбираем двигатель:

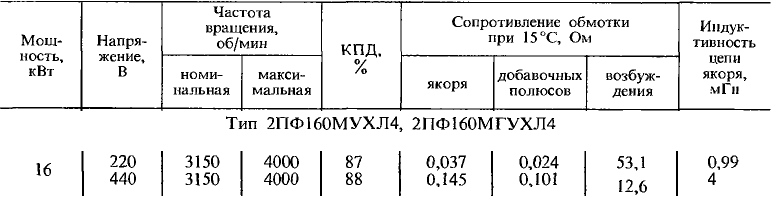
Передаточное число редуктора

j_Р= _Н/_М.МАКС = 329,2/230 =1,43

где _Н 0,1045 n _Н = 0,1045*3150 =329,2– номинальная угловая скорость двигателя, n _Н - номинальное число оборотов вала в минуту.

М_Н = Р_Н/_Н = 16000/329,2= 48,603Н*м.

Для проверки выбранного двигателя определяют эквивалентный момент:

М_Э =

М_Э =

Суммарный момент инерции двигателя с редуктором:

J₁=J_Д + J_P = J_Д + 0,1 J_Д = 1,1 J_Д

J₁ =1,1*0,083=0,0913

где J_Д , J_P - соответственно моменты инерции двигателя и редуктора.

Суммарный момент инерции электропривода:

J =  J₁=0,3*0,0913=0,0274

Максимальное ускорение вала двигателя:

 _МАКС =  _М.МАКС j_Р =100*1,43=143

2. Структурная схема трехмассовой упругой системы:

Решив биквадратное уравнение, получаем корни характеристического

уравнения системы:

p₁ =0

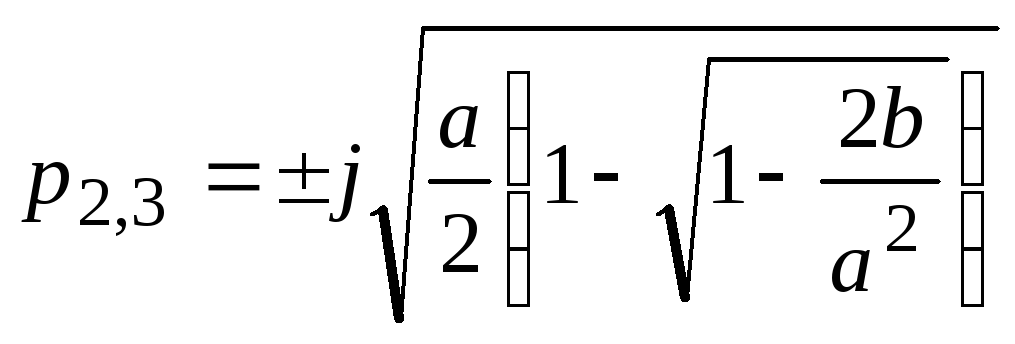
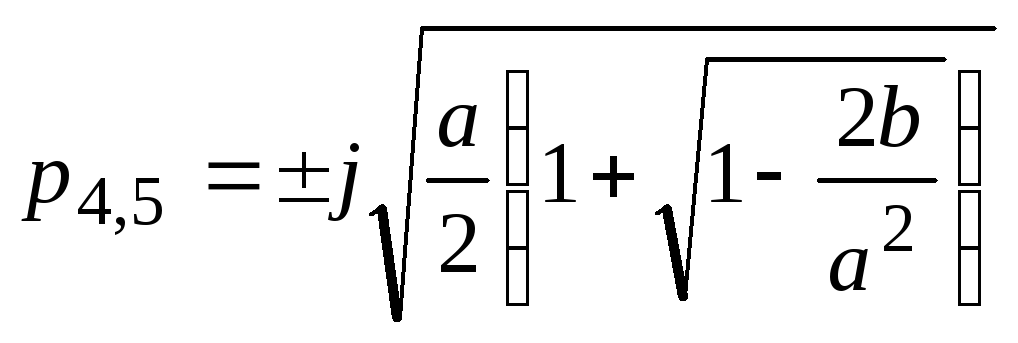
где

Анализ корней показывает, что при всех реальных сочетаниях параметров подкоренные выражения представляют собой действительные положительные числа.

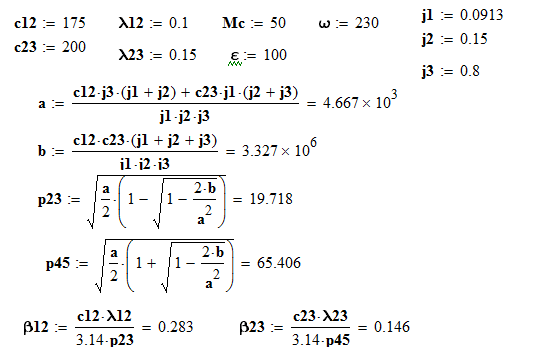
График зависимости ₁(t)

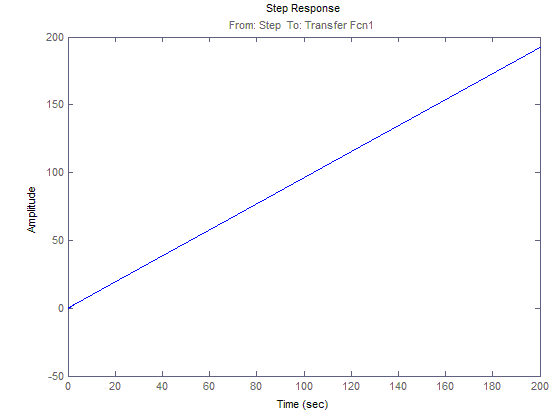
ЛАЧХ и ЛФЧХ для ₁(t)

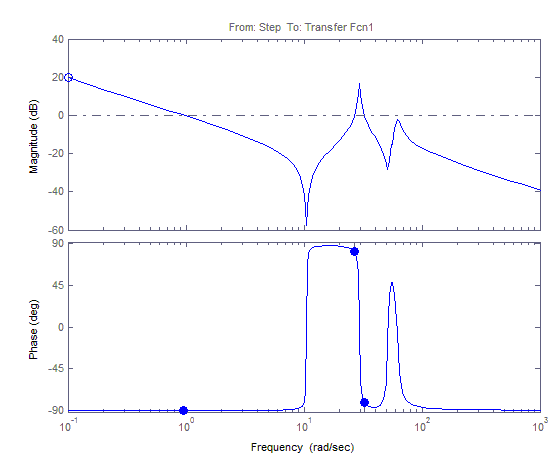
АФЧХ для ₁(t)

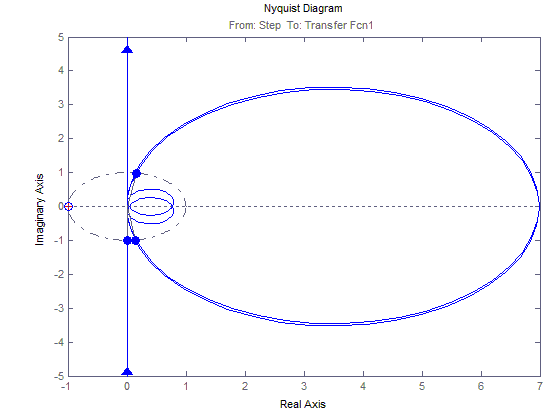
График зависимости ₂(t)

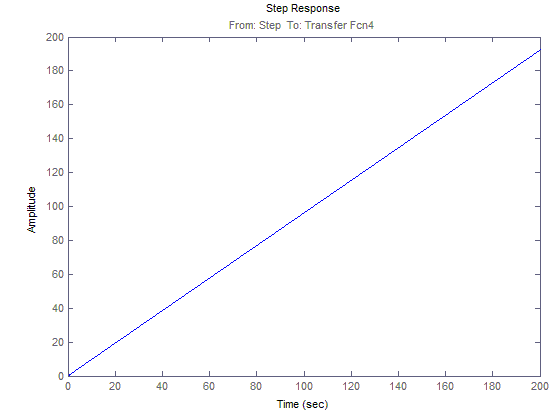
ЛАЧХ и ЛФЧХ для ₂(t)

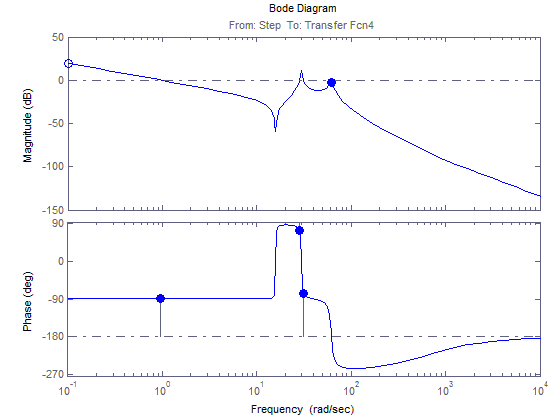
АФЧХ для ₂(t)

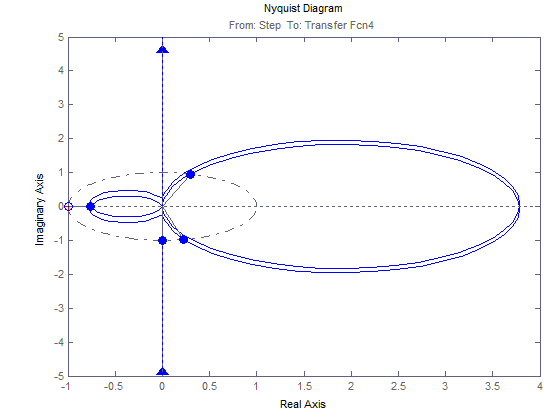
График зависимости ₃(t)

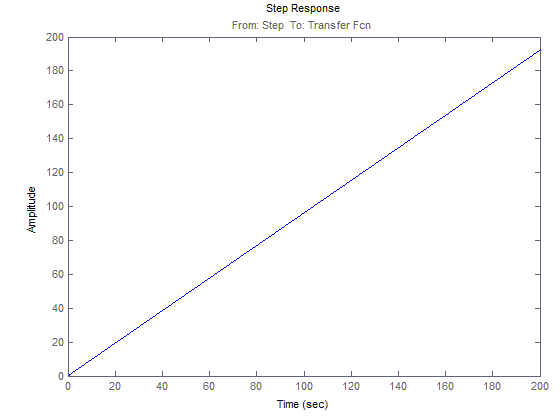
ЛАЧХ и ЛФЧХ для ₃(t)

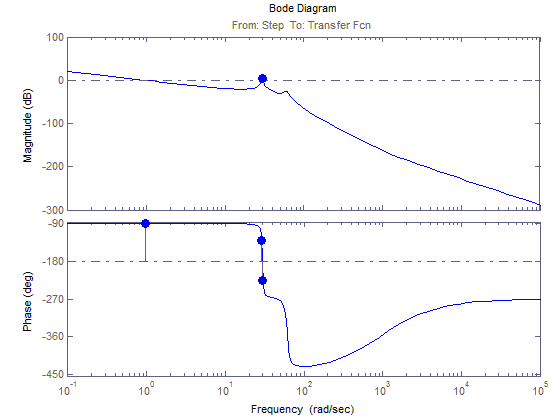
АФЧХ для ₃(t)

График зависимости М₁₂(t)

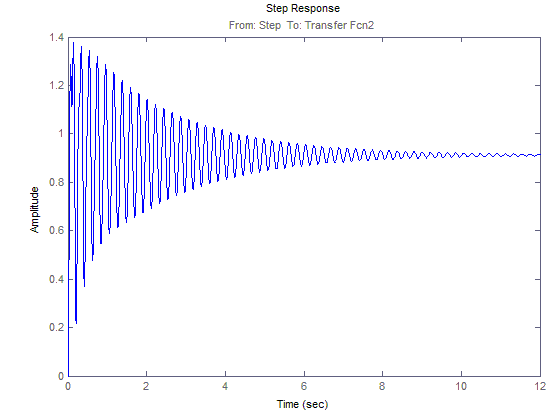
ЛАЧХ и ЛФЧХ для М₁₂(t)

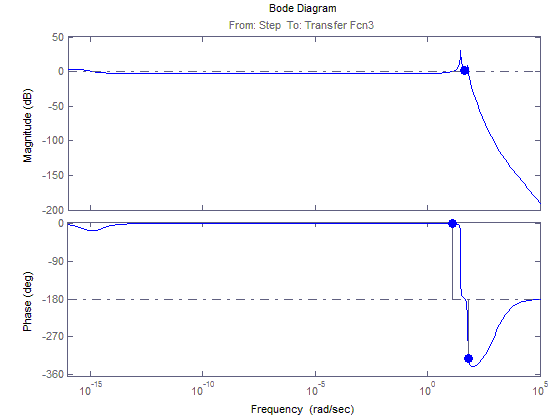
АФЧХ для М₁₂(t)

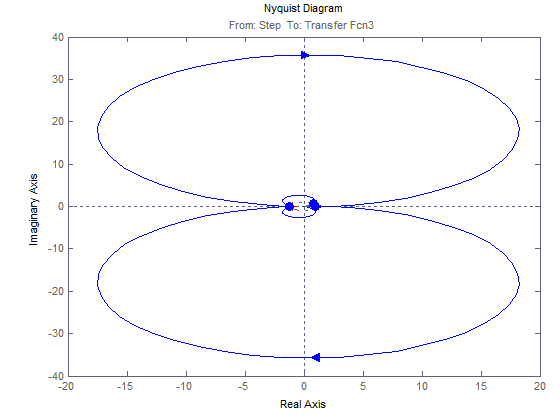
График зависимости М₂₃(t)

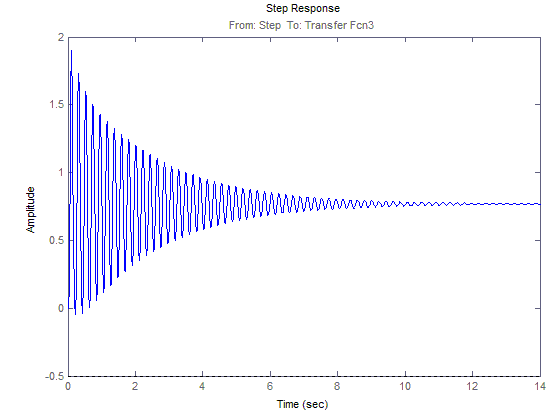
ЛАЧХ и ЛФЧХ для М₂₃(t)

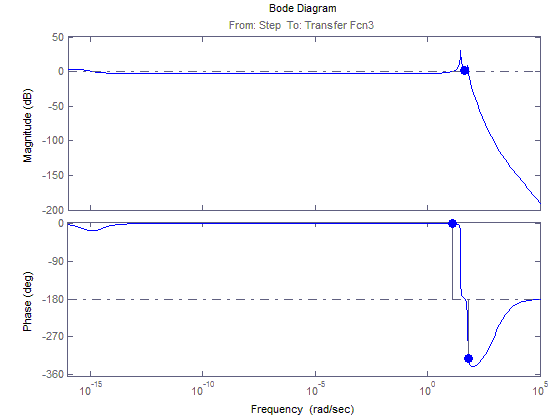
АФЧХ для М₂₃(t)

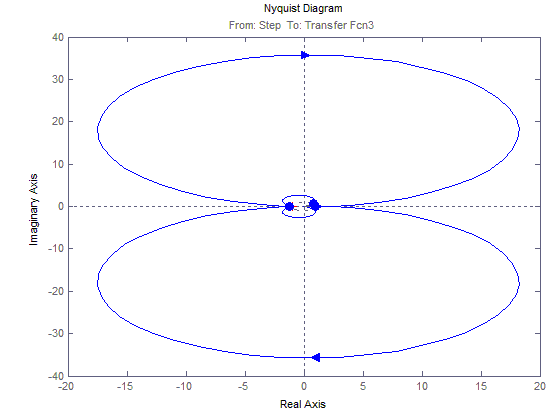
Э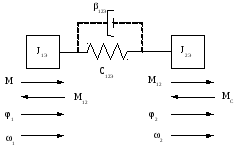квивалентная расчетная схема двухмассовой упругой механической системы.

Приведение к двухмассовой системе:

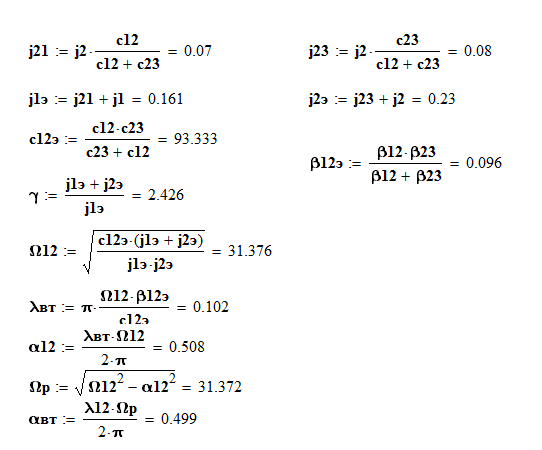
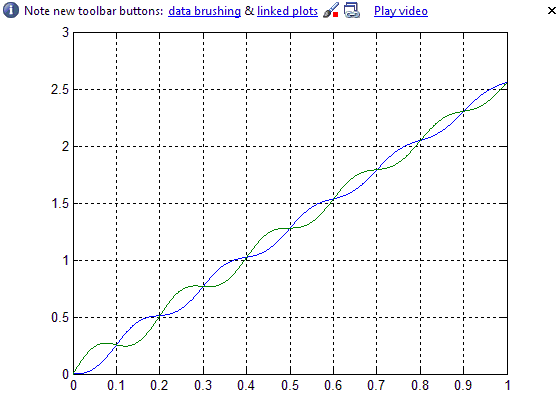
График зависимости ₁(t)

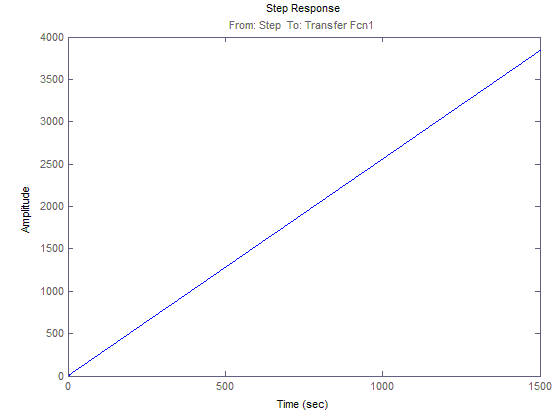
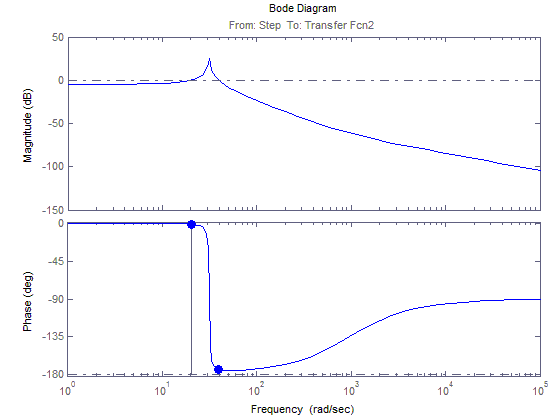
ЛАЧХ и ЛФЧХ для ₁(t)

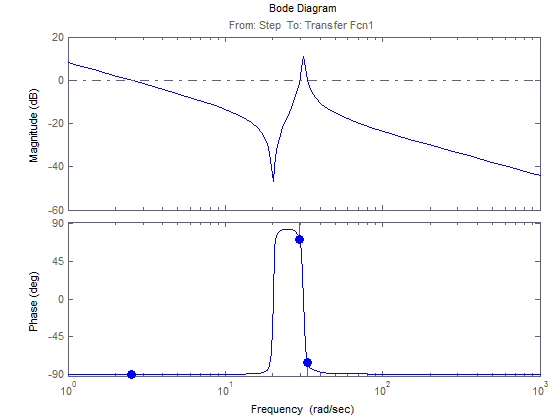
АФЧХ для ₁(t)

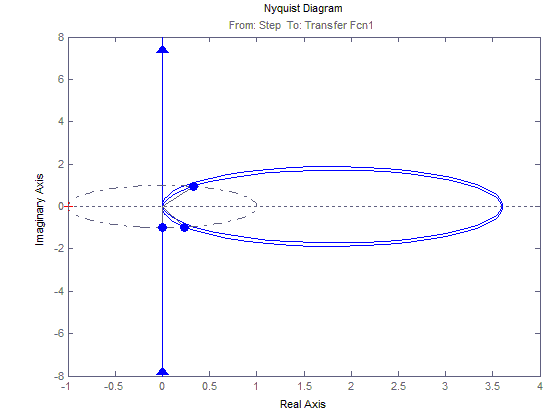
График зависимости ₂(t)

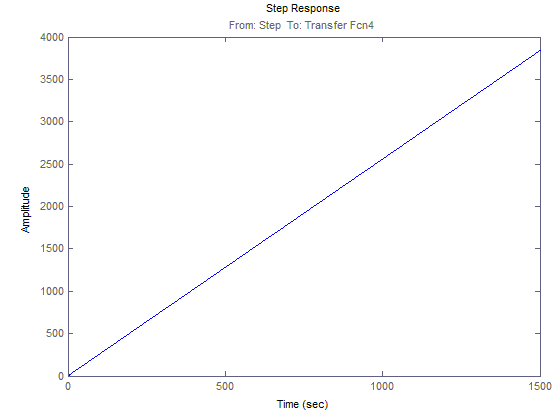
ЛАЧХ и ЛФЧХ для ₂(t)

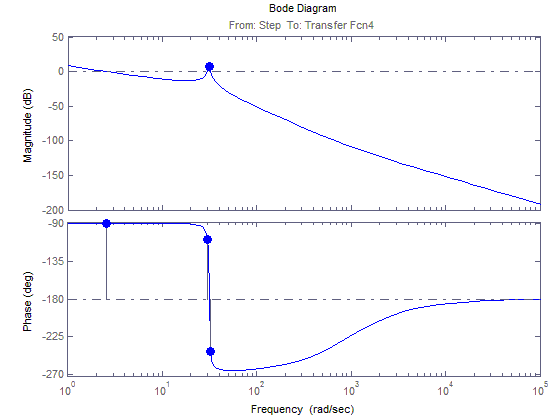
АФЧХ для ₂(t)

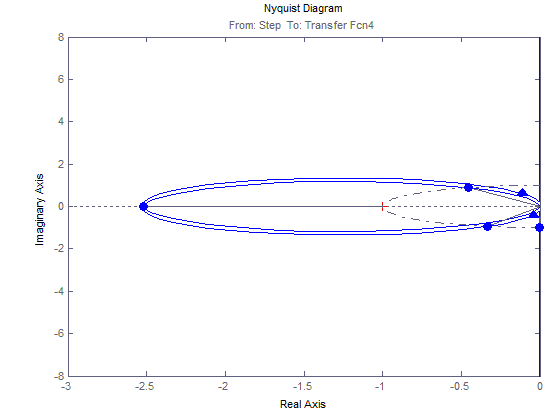
График зависимости М₁₂(t)

ЛАЧХ и ЛФЧХ для М₁₂(t)

АФЧХ для М₁₂(t)

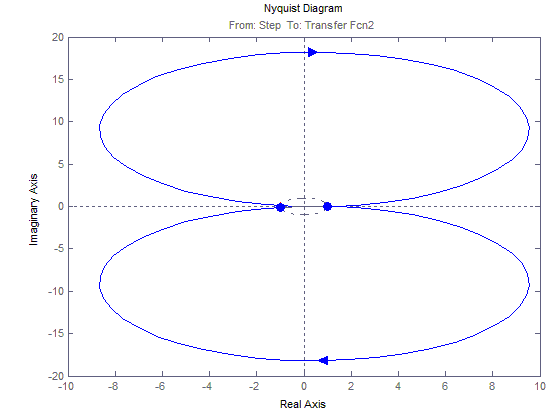
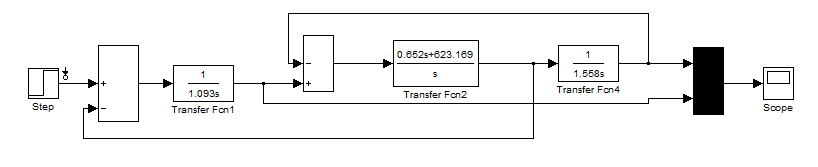
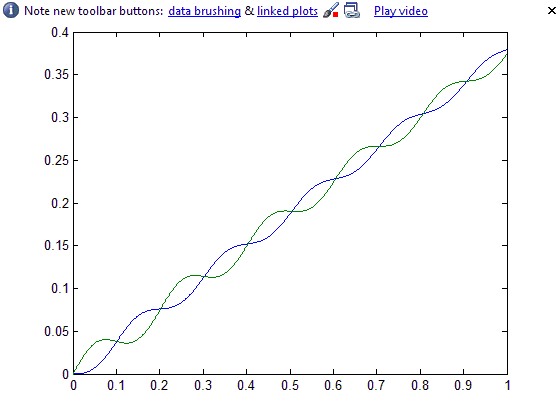
График зависимости ₁(t)

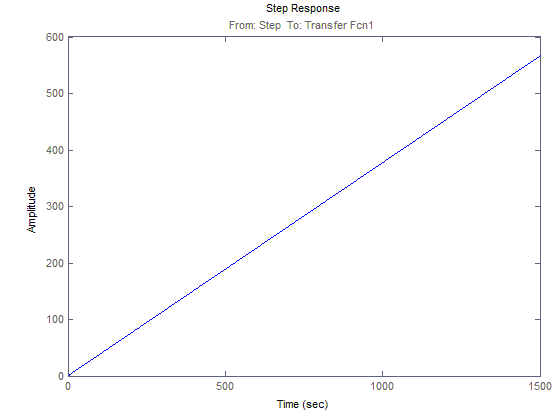
ЛАЧХ и ЛФЧХ для ₁(t)

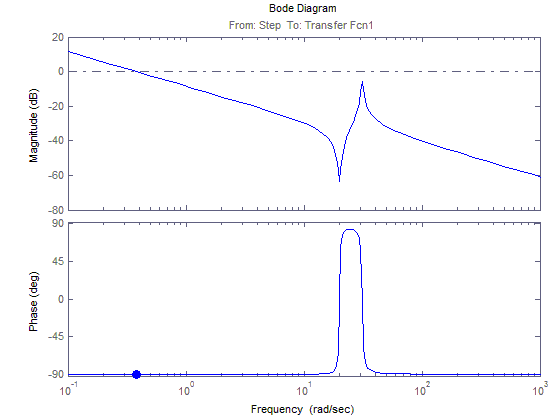
АФЧХ для ₁(t)

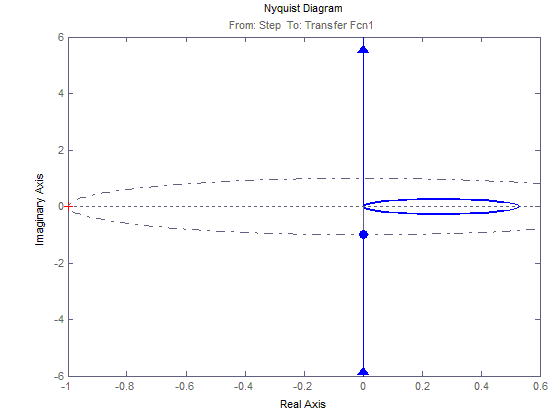
График зависимости ₂(t)

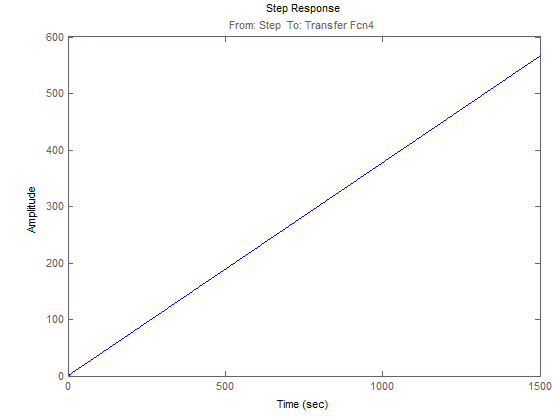
ЛАЧХ и ЛФЧХ для ₂(t)

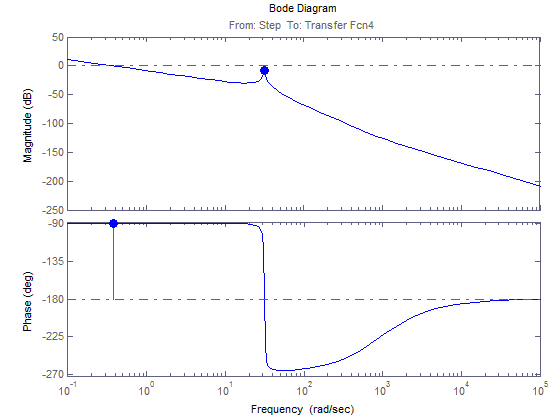
АФЧХ для ₂(t)

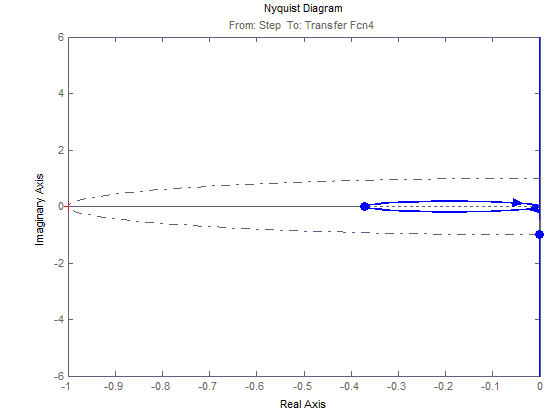
График зависимости М₁₂(t)

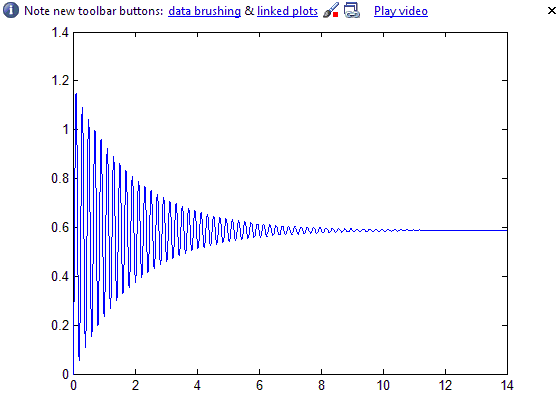
ЛАЧХ и ЛФЧХ для М₁₂(t)

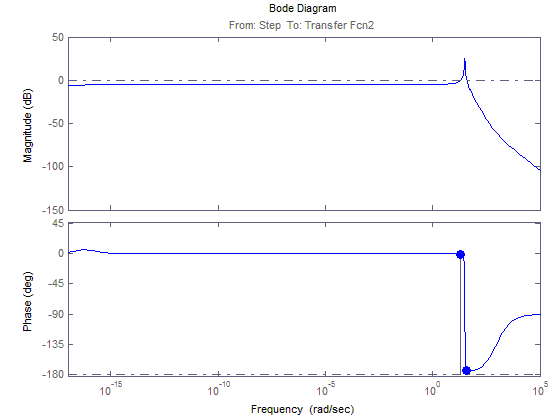
АФЧХ для М₁₂(t)

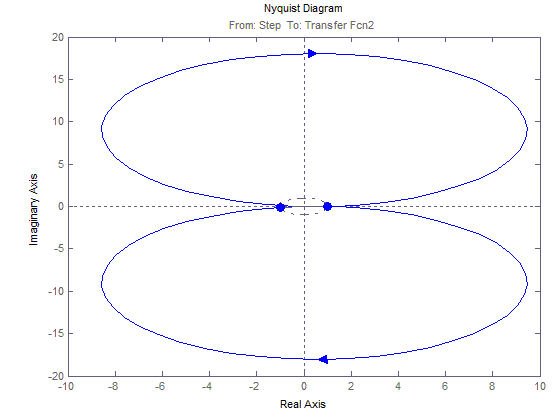
Осуществить варьирование параметров двухмассовой механической системы и выявить их влияние на частотные и временные характеристики объекта моделирования, параметры МЧ ЭП изменить в пределах (1…3) J₂

1)1.5J₂

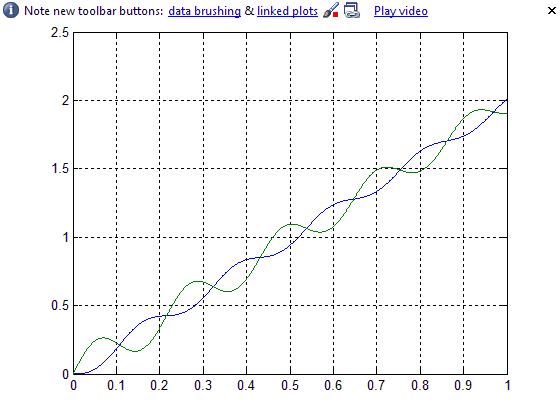
2)3J₂

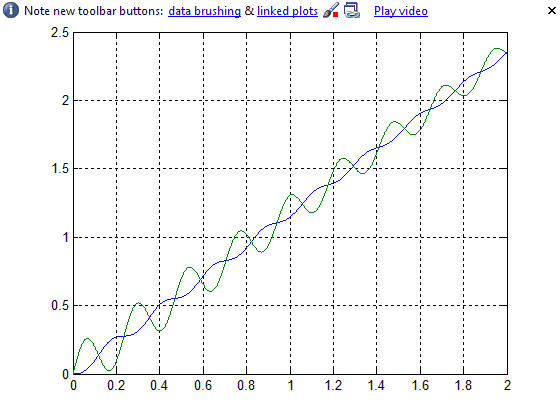
и (0,5…1,5) С₁₂

3)0.5C₁₂

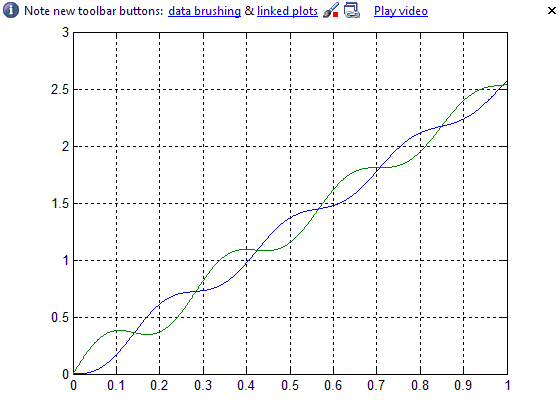
4)1.5C₁₂