
2 лекция по физике
.pdf
16.02.2012
Лекция № 2 Физические основы механики
Кинематика и динамика материальной точки
Курс общей физики в 3-х томах, том I. Механика, колебания и волны, молекулярная физика. / И. В. Савельев. - М.: «Наука», 1970. - 511 с.
2Кинематика вращательного движения
1
16.02.2012
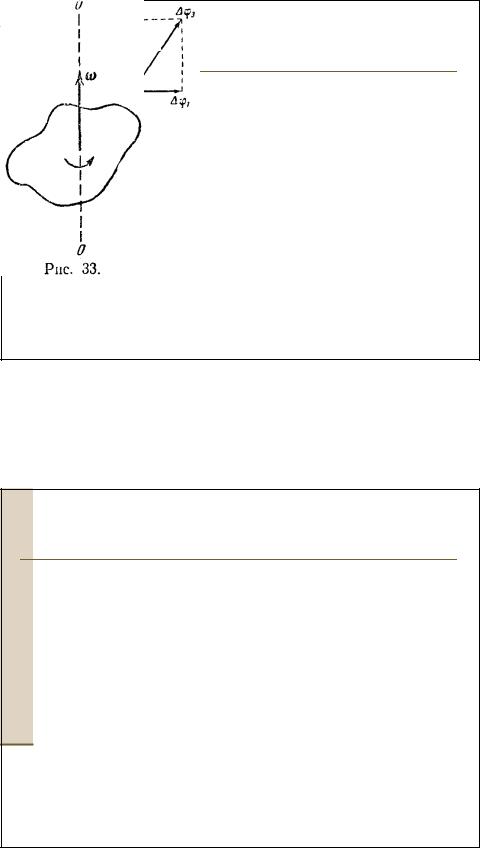
3Кинематика вращательного движения
4Кинематика вращательного движения
ω lim |
φ |
dφ |
(1.28) |
|
t 0 |
t |
dt |
|
|
|
2 |
|
(1.29) |
|
|
T |
|
|
|
T |
2 |
|
(1.30) |
|
|
|
|
|
|
2

16.02.2012
5Кинематика вращательного движения
|
1 |
|
|
|
|
(1.31) |
|
2 |
|
||||
|
T |
|
|
|||
2 |
(1.32) |
|||||
β lim |
ω |
d |
(1.33) |
|||
|
t 0 |
t |
dt |
|
||
6Кинематика вращательного движения
s R
v lim |
s lim R |
|
|
|
t 0 |
t |
t 0 |
t |
|
R lim |
|
R d |
R , |
|
t 0 |
t |
dt |
|
|
т. е. |
|
|
|
|
v R |
|
(1.34) |
||
3

16.02.2012
7Кинематика вращательного движения
n v2
R
n 2 R |
(1.35) |
|
|
|
|
||||||||||||
|
|
lim v |
|
|
|
R |
|
|
|||||||||
|
|
lim |
|
|
|||||||||||||
|
|
||||||||||||||||
|
|
t 0 t |
|
t 0 |
t |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
lim R |
|
|
|
R |
|
lim |
|
|
R , |
|||||||
|
|
|
|
||||||||||||||
|
t 0 |
|
t |
|
|
|
|
|
t 0 |
t |
|
|
|
|
|||
т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
(1.36) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 Связь между векторами v и ω
C ABsin
AB или |
A B |
AB BA
4

16.02.2012
9 Связь между векторами v и ω
D A, |
|
BA |
|
|
|
|
|
D A, |
BA A2B (1.37) |
||
|
|
|
|
10 Связь между векторами v и ω
r sin R v
v ωr (1.38)
r rz R
|
ωr |
|
z |
|
z |
|
ωR |
|
|
|
ω r |
R |
ωr |
|
|
||
|
|
v ωR |
(1.39) |
|
|
|
||
5

16.02.2012
11Динамика материальной точки
Первый закон Ньютона
•Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Или иначе:
•скорость любого тела остается постоянной, пока воздействие на это тело со стороны других тел не вызовет ее изменения.
12Инерциальные системы отсчета
•Система отсчета, в которой выполняется закон Ньютона, называется инерциальной, а в которой он не выполняется называется неинерциальной.
•Примером инерциальной системы является гелеоцентрическая система, в которой центр совмещен с Солнцем
•Любая система отсчета движущаяся равномерно и прямолинейно относительно гелеоцентрической системы, будет инерциальной
6

16.02.2012
13Второй закон Ньютона
•Второй закон Ньютона формулируется следующим образом:
ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела.
k |
|
f |
|
(1.40) |
|
m |
|||||
|
|
||||
ω k |
|
f |
(1.41) |
||
|
m |
||||
|
|
|
|||
14Третий закон Ньютона
•Третий закон Ньютона формулируется следующим образом:
всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению.
f12 f21 |
(1.42) |
7

16.02.2012
15 Импульс
• Уравнению второго закона Ньютона
|
m |
dv |
f |
(1.43) |
|
|
|
|
|||
|
|
dt |
|
||
• Можно придать другой вид |
|||||
|
|
|
d mv |
f |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
• |
Векторную величину |
||||
|
p mv |
(1.44) |
|||
• |
называют импульсом материальной точки |
||||
16Импульс
•Используя определение импульса, уравнение 2-го закона Ньютона можно записать как:
dp |
f |
(1.45) |
|
dt |
|||
|
|
•а сам второй закон сформулировать так:
производная импульса материальной точки по времени равна результирующей всех сил, действующих на точку
8

16.02.2012
17 Импульс
• Умножив (1.45) на dt, придем к
соотношению: |
|
dp fdt |
(1.46) |
• интегрирование которого дает приращение импульса за время от t1 до t2
p |
2 |
p |
|
|
dp t2 fdt |
(1.47) |
|
1 |
|
|
t1 |
|
|
|
|
|
|
|
• если f = constant, то интегрирование дает приращение импульса за время τ:
p2 p1 f
18 Закон сохранения импульса
• Импульсом системы р называется векторная суммы импульсов тел, образующих систему,
N
p p1 p2 ... pN pi
i 1
• Назовем центром инерции системы точку, положение которой в пространстве задается радиусом-вектором rc, определяемым следующим образом:
r |
m1r1 m2r2 |
... mN rN |
miri miri |
(1.48) |
||
|
|
|||||
c |
m1 |
m2 |
... mN |
mi |
m |
|
|
|
|||||
9

16.02.2012
19Закон сохранения импульса
•Декартовы координаты центра инерции равны проекциям rс на координатные оси:
x |
|
mi xi ; y |
c |
mi yi ; z |
c |
mi zi |
(1.49) |
c |
|
m |
m |
m |
|
||
|
|
|
|
|
• Отметим, что центр инерции совпадает с центром тяжести системы.
• Скорость центра инерции получается путем дифференцирования rс по времени:
vc rc miri mi vi
m m
20Закон сохранения импульса
•Учитывая, что mivi есть рi , а ∑рi дает импульс системы р, можно написать
p mvc |
(1.50) |
•Таким образом, импульс системы равен произведению массы системы на скорость ее центра тяжести
10
