
Mehanika_zhidkosti_i_gaza_Praktika
.pdf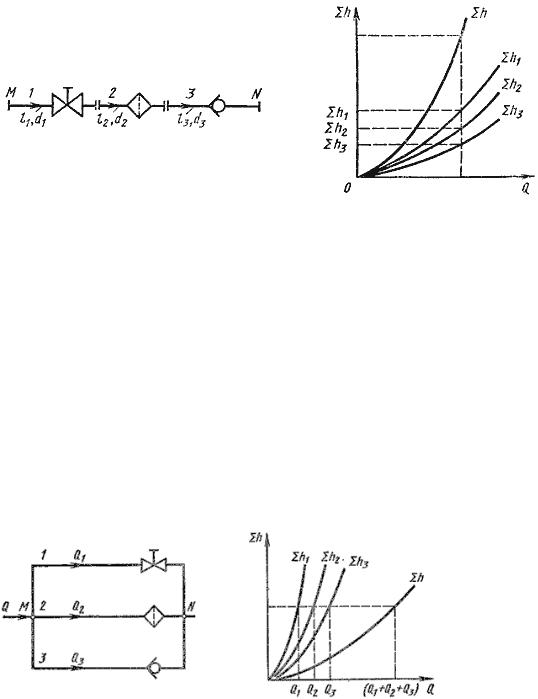
4 РАСЧЁТ ТРУБОПРОВОДОВ
Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным или параллельным.
Последовательное соединение
Рисунок 10 – Последовательное соединение трубопроводов
Расход во всех трубопроводах при последовательном соединении одинаков
Q = Q1 = Q2 = Q3 |
(14) |
Общее сопротивление равно сумме всех сопротивления |
|
∑hпотерь = ∑h1 + ∑h2 + ∑h3 |
(15) |
Параллельное соединение
Рисунок 11 – Параллельное соединение трубопроводов
21

Общий расход равен сумме расходов через все трубопроводы
Q = Q1 + Q2 + Q3 |
(16) |
Суммарные сопротивления всех трубопроводов равны, т.к. в тех трубопроводах, где препятствий течению больше, жидкость течёт медленнее
∑h1 = ∑h2 = ∑ h3 |
(17) |
Трубопроводы с насосной подачей
При установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному напору, т.е. насос и сеть находятся в равновесии.
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q) и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рисунок 12).
Рисунок 12 – Графическое нахождение рабочей точки а - турбулентный режим; б - ламинарный режим
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса.
Рабочая точка – точка пересечения кривой потребного напора с характеристикой насоса.
Как подобрать насосную станцию http://www.youtube.com/watch?feature=player_detailpage&v=S9TNiyWUrkE
Обслуживание трубопроводов http://www.youtube.com/watch?feature=player_detailpage&v=5kbf2dv3owY
22

Интерактивный обучающий ресурс посвященный конструированию и расчёту насосов http://www.isuct.ru/dept/chemkiber/piaht/edu/index.php?page=intro.inc
Пример 6
Для регулирования расхода воды в охлаждающем змеевике использован байпас (в отличие от дроссельного регулирования при этом не возрастает суммарное гидравлическое сопротивление системы). Насос работает с постоянной производительностью Q. Змеевик и все трубопроводы изготовлены из трубы диаметром d. Змеевик состоит из n витков, свёрнутых в цилиндрическую спираль диаметром D. Длина змеевиковой линии L1 (без учёта длины самого змеевика), длина байпасной линии L2. Шероховатость труб ∆ = 0,2 мм. Режим течения во всей системе считать развитым турбулентный Re = 1000000. Перепадом высот пренебречь.
Таблица 2 – |
Коэффициент местного сопротивления регулировочного |
||||||
крана ζкр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Угол |
|
|
|
|
|
|
|
прикрытия |
10 |
|
20 |
30 |
40 |
50 |
60 |
α, о |
|
|
|
|
|
|
|
ζ |
0,3 |
|
1,6 |
5,5 |
17,5 |
52, 5 |
215 |
Определить как изменится расход через змеевик при полностью открытом кране, при прикрытии крана на 20 о, 60 о и при полностью закрытом кране.
Рисунок 13 – Байпасное регулирование
--- байпасная линия, --- змеевиковая линия, --- змеевик, змеевиковая линия и сам змеевик образуют основную линию
23

Решение
Змеевик представляет собой трубу свёрнутую кольцами, поэтому его сопротивление будет определяться также как и для прямых труб, но с учётом изогнутости.
Длина змеевика – это сумма длин всех его колец
LЗМ = n ×πD
Поправочный коэффициент для сопротивления изогнутой трубы
ϕ = 1 + 3,54 |
d |
(18) |
|
D |
|||
|
|
Сопротивление змеевика с учётом формулы Дарси (10) и поправочного коэффициента (18)
|
|
|
d nπD vзм |
2 |
||||
hЗМ |
= λ 1 |
+ 3,54 |
|
|
|
|
|
|
|
d 2g |
|||||||
|
|
|
D |
|||||
Сопротивление в змеевиковой линии
hL1 |
= λ |
L |
|
v 2 |
1 |
|
зм |
||
|
|
|
||
|
|
d |
|
2g |
Общее сопротивление основной линии
|
|
= λ |
|
|
d nπD vзм |
2 |
|
+ λ |
|||||||||||
Sh1 = hЗМ + hL1 |
1+ |
3,54 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
d |
|
|
2g |
|
||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
d |
|
nπD |
|
|
|
|
L1 |
||||||
Обозначив |
|
|
|
λ 1 |
+ 3,54 |
|
|
|
|
|
|
|
|
+ |
λ |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
D |
d |
|
|
|
|
d |
||||||
|
|
2g |
|
|
|
|
|
|
|||||||||||
Sh1 = k1 × vзм2
L1 |
|
vзм |
2 |
|
1 |
|
|
|
|
|
|
|
= |
|
|
λ 1 |
+ 3,54 |
|
|
|
|
|
||||
d |
|
2g |
|
|
|
|
||
|
2g |
|
||||||
за k , получим
1
d nπD |
+ λ |
L1 |
|
|
2 |
||
|
|
|
|
|
×v |
зм |
|
|
|
|
|||||
D |
d |
|
|
|
|
|
|
|
d |
|
|
||||
Для определения значения λ при Re = 106 воспользуемся графиком на
d
рисунке 8, предварительно вычислив отношение D .
Линейное сопротивление байпасной линии
2
hбайп = λ Lбайп vбайп
d 2g
24

Местное сопротивление крана
2
hкр = ζ vбайп
2g
Суммарное сопротивление байпасной линии
|
|
Lбайп |
2 |
|
vбайп |
2 |
|
1 |
|
|
Lбайп |
|
|
|
|
|
|
vбайп |
|
|
|
|
2 |
||||||
Σh2 = hбайп + hкр |
= λ |
|
|
|
+ ζ |
|
|
= |
|
|
λ |
|
+ ζ vбайп |
|
d |
|
2g |
2g |
|
|
d |
|
|||||||
|
|
|
|
|
|
2g |
|
|
|
|||||
|
1 |
|
|
|
Lбайп |
|
Обозначив |
|
|
λ |
|
|
+ ζ за k2, получим |
|
|
|
||||
|
2g |
|
|
d |
|
|
Sh2 = k2 × vзм |
2 |
|
||||
Теперь воспользуемся соотношениями (16) и (17) для параллельного соединения трубопроводов
∑h1 = ∑h2
Следовательно
k1vзм2 = k2 vбайп 2
Общий расход равен сумме расходов через змеевик и байпас
Q = Qзм + Qбайп
Q = πd 2 vзм + πd 2 vбайп
4 4
Получили систему двух уравнений с двумя неизвестными
k v |
|
2 = k v |
|
2 |
|
|
1 |
зм |
|
2 |
байп |
|
|
|
|
|
2 |
|
|
2 |
Q = πd |
|
πd |
||||
vзм + |
vбайп |
|||||
|
|
4 |
|
|
4 |
|
Выражая из второго уравнения скорость потока в байпасе и подставляя ее в первое выражения получаем
25

|
|
|
|
πd |
2 |
|
|
2 |
|
|
Q − |
|
v |
|
|
||
|
2 |
|
|
4 |
|
зм |
||
k1v |
|
= k2 |
|
|
|
|
|
|
зм |
|
πd |
2 |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Или
|
|
|
2 |
= k |
|
|
|
|
4Q |
|
− v |
2 |
|
|
|
|
|
|
|
|
|
|
|||
k |
v |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||
зм |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
πd |
|
|
зм |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Раскрываем квадрат разницы |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= k |
|
|
|
4Q |
− |
|
4Q |
|
|
|
|
+ v |
|
2 |
|||||||
k |
v |
зм |
|
2 |
|
|
|
|
2 |
|
|
2 |
|
2 |
|
v |
зм |
зм |
|||||||
1 |
|
|
|
|
πd |
|
|
|
πd |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получаем квадратное уравнение |
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
4Q |
|
|
|
|
|
4Q |
|
2 |
||||||||
(k1 − |
1)vзм |
|
+ |
2k2 |
|
|
|
v |
зм − k2 |
|
|
|
|
|
= 0 |
||||||||||
|
πd 2 |
πd 2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Сгруппировав и обозначив коэффициенты перед неизвестной скоростью
(k1 − 1) = a
4Q =
2k b
2 πd 2
|
|
4Q |
|
2 |
|
− k |
|
|
|
|
= c |
|
πd 2 |
||||
|
2 |
|
|
|
|
avзм 2 + bvзм + c = 0
Корни уравнения
vзм1,2 = − b ± 
 b2 − 4ac
b2 − 4ac
2a
При выборе корня необходимо руководствоваться физическими соображениями.
26
Теперь можно рассчитать скорость для всех случаев, и умножив её на площадь поперечного сечения трубы получить расходы. При полностью закрытом кране течения в байпасной линии не будет, и расход в змеевике будет равен производительности насоса. В случае полного открытия кран представляет собой обыкновенную трубу, тогда коэффициент местного сопротивления равен нулю.
27
ИСТОЧНИКИ
1Кострюков В.А. Основы гидравлики и аэродинамики. Под ред. С.В. Каплинского. Учебник для техникумов. М., «Высшая школа», 1975 – 220 с.
2Касаткин А.Г. Основные процессы и аппараты химической технологии. Учебник для вузов - 10-е изд., стереотипное, доработанное.
Перепеч. с изд. 1973 г. — |
М.: ООО ТИД «Альянс», 2004. — 753 с. |
3 Шабловский А.С. |
Выполнение домашних заданий и курсовых работ |
по дисциплине «Механика жидкости и газа» : учеб. пособие: В 2 ч. - Ч. 2:
Гидродинамика. |
— 2- |
е изд., испр. и доп. |
— |
М. : Изд-во МГТУ им. Н. Э. |
Баумана, 2012. — 65 |
с. |
|
|
|
4 Работа |
центробежного насоса |
в |
трубопроводной сети. Ресурс |
|
Ивановского государственного химико-технологического университета http://www.isuct.ru/dept/chemkiber/piaht/edu/index.php?page=intro.inc
5 Образовательный ресурс по гидравлике, гидро- и пневмоприводу. http://gidravl.narod.ru/index1.html
28
