
Mehanika_zhidkosti_i_gaza_Praktika
.pdf
МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Санкт-Петербургский государственный технологический институт (технический университет)»
(СПбГТИ(ТУ))
Кафедра машин и аппаратов химических производств
М.А. Ратасеп
МЕХАНИКА ЖИДКОСТИ И ГАЗА
Методические указания к практическим занятиям для студентов заочников
Санкт − Петербург
2013
УДК 66.02(075)
Ратасеп М.А. Механика жидкости и газа: методические указания к практическим занятиям / М.А. Ратасеп− СПбГТИ (ТУ), 2013. 28 с.
Излагаются теоретические основы механики жидкости и газа. Приводятся примеры расчета типовых задач. Даны ссылки на мультимедийные ресурсы.
Предназначено для студентов заочной формы обучения по направлению 151000 Технологические машины и оборудование, и соответствует рабочей программе по дисциплине « Машины и аппараты переработки нефти и газа»
Табл. 2, библиография 5 наз.
Рецензент:
Утверждены |
на |
заседании |
учебно-методической |
коммиссии |
||
механического факультета |
|
|
|
2013 |
|
|
Рекомендовано к изданию РИСоСПбГТУ(ТУ)
2
Содержание
1 |
Гидростатика ........................................................................................... |
4 |
|
Пример 1 ................................................................................................. |
5 |
2 |
Основы гидродинамики .......................................................................... |
7 |
|
Пример 2 ............................................................................................... |
11 |
|
Пример 3 ............................................................................................... |
12 |
|
Пример 4 ............................................................................................... |
14 |
3 |
Гидравлические сопротивления ........................................................... |
16 |
|
Пример 5 ............................................................................................... |
19 |
4 |
Расчёт трубопроводов ........................................................................... |
21 |
|
Пример 6 ............................................................................................... |
23 |
Источники................................................................................................. |
28 |
|
3

1 ГИДРОСТАТИКА
Закон Паскаля: давление, оказываемое на жидкость, передаётся жидкостью одинаково во всех направлениях (пример: сообщающиеся сосуды).
Основной закон гидростатики: давление в толще жидкости зависит
от глубины. |
|
p = ρ × g × H , |
(1) |
где ρ – плотность жидкости, g – ускорение свободного падения.
Закон Архимеда: на тело, погружённое в жидкость, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
FА = ρ × g ×V , |
(2) |
где V – объём части тела, погружённой в жидкость.
Если тело однородно, и полностью погружено в жидкость, то равнодействующая силы тяжести и силы Архимеда, будет определяться разностью плотностей жидкости и тела.
Fвыт = g ×V × (ρ - ρ м ) |
(3) |
Закон Паскаля
http://www.youtube.com/watch?feature=player_detailpage&v=0BoWQQ8AVBQ
Демонстрация опыта с сосудом Архимеда:
http://www.youtube.com/watch?feature=player_detailpage&v=rpPsnUqEtW0
Подводные лодки и закон Архимеда:
http://www.youtube.com/watch?feature=player_detailpage&v=SkvaKBMgwWc
4
Пример 1
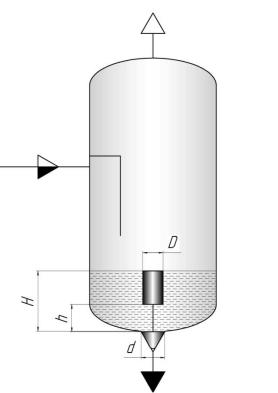
Отработанная парогазовая смесь конденсируется в сепараторе. Газ уходит вверх, сконденсировавшаяся жидкость сливается вниз. Для того чтобы газ не попал в слив, сливной клапан открывается только тогда, когда жидкость в аппарате достигает определённого уровня. Автоматизация работы клапана реализована с помощью поплавка соединённого штоком с клапаном. Верхний край поплавка совпадает с поверхностью жидкости. Поплавок имеет цилиндрическую форму. Плотность конденсата ρ, плотность материала поплавка ρп , диаметр поплавка D, диаметр клапана d, длина штока h, масса поднимаемого клапанного механизма m.
Рисунок 1 – Схема сепаратора
Определить минимальный уровень жидкости H в сепараторе и высоту поплавка, при которых клапан откроется.
Решение
Из рисунка видно, что высоту поплавка можно определить как H-h.
Сила, вытесняющая поплавок вверх, равна разности плотностей тела, погружённого в жидкость, и плотности самой жидкости, умноженных на вытесненный объём и на ускорение свободного падения g.
5

Поплавок по условию задачи полностью погружён в жидкость, следовательно, объём вытесненной жидкости совпадает с его объёмом.
Равнодействующая силы Архимеда и силы тяжести поплавка
Fвыт = g ×V ×(ρ - ρп )
Объём поплавка
V = πD 2 × (H - h)
4
Сила гидростатического давления, действующая на клапан и препятствующая его открытию
Fг = ρgH × πd 2
4
Условием открытия клапана является превышение силы, выталкивающей поплавок вверх, силы тяжести поднимаемого клапана и силы гидростатического давления, действующей на клапан:
FA ³ G + Fg |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
g × πD 2 (H - h)× (ρ - ρ |
м ) ³ G + ρgH × πd 2 |
||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
πd 2 |
2 |
4 |
|
||||||||
(H - h)× ³ G + ρgH × |
|
|
|
× |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× (ρ - ρ м ) |
||||
|
|
|
|
|
|
|
|
|
|
4 g ×πD |
|
||||||||
(H - h) ³ G |
|
|
4 |
|
|
|
|
|
|
+ H × |
|
ρd 2 |
|||||||
g ×πD 2 × (ρ - ρ м ) |
D 2 (ρ - ρ м ) |
||||||||||||||||||
|
h + G |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
H ³ |
gπD 2 |
(ρ - ρ |
м ) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ρd 2 |
|
|
|
|
|
|
|
|
|
||||
1 - |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
D 2 (ρ - ρ м ) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
G = m × g |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
h + |
|
|
|
|
|
4m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
H ³ |
πD 2 |
(ρ - ρ м ) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ρd 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
D 2 (ρ - |
ρ м ) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6
2 ОСНОВЫ ГИДРОДИНАМИКИ
Удобно представить поток жидкости системой струек. Можно предположить, что есть воображаемая система трубок, по которым течёт жидкость, форма трубок повторяет траектории течения жидкости. Так же как в реальных трубах, жидкость течет только по трубкам и не может перетекать из одной в другую через стенку.
Линия тока – кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой.
При установившемся движении линии тока совпадают с траекториями движения частиц жидкости.
Трубка тока – бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.
Элементарной струйкой называется часть потока, заключенная внутри трубки тока.
Трубка тока является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.
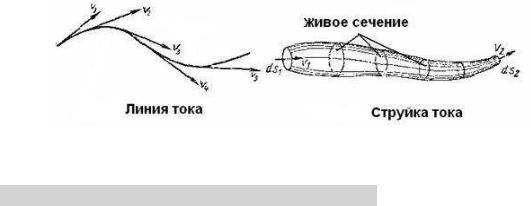
Живое сечение или сечение потока – площадь поверхности в пределах потока или струйки, проведенная нормально к линиям тока.
Рисунок 2 – Линии тока, живое сечение и струйка тока
Компьютерная симуляция потока воды в трубе http://www.youtube.com/watch?feature=player_detailpage&v=vEu8aE9MsjA
Уравнение постоянства расхода (неразрывности потока)
Q = v1S1 = v2 S2 = const , |
(4) |
где v1, v2 – средние скорости, S1, S2 – площади живых сечений потока.
7

Объяснение основных понятий гидродинамики и вывод уравнения Бернулли http://www.youtube.com/watch?v=9_oRZDivCpw&feature=player_detailpage
Уравнение Бернулли
Энергия жидкости состоит из трёх составляющих: внешнего давления p (статический или пьезометрический напор), потенциальной энергии (весовой напор или нивелирная высота) и кинетической энергии (динамический или скоростной напор).
Потенциальная энергия тела поднятого на высоту H
Eпот* = mgH
Кинетическая энергия тела, движущегося со скоростью v
Eкин* = mv2
2
Для жидкости удобней перейти от массы к плотности, тогда удельная потенциальная энергия жидкости на уровне H
Eпот = ρgH
Удельная кинетическая энергия жидкости, движущейся со скоростью v
Eкин = ρv2
2
Согласно закону сохранения энергии полный запас энергии жидкости должен оставаться неизменным:
|
|
p + ρgH + |
ρv2 |
|
= const |
|
|
|
|
|
|
(5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Иногда удобно перейти от энергии к напору – |
энергии выраженной в |
|||||||||||||||||||
единицах высоты столба жидкости: |
|
|
|
||||||||||||||||||
|
|
|
p |
+ H + |
v 2 |
|
= const |
|
|
|
|
|
|
(5’) |
|||||||
|
|
ρg |
2g |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
||
где |
|
– |
пьезометрический напор, H – невелирная высота, |
|
– скоростной |
||||||||||||||||
ρg |
2g |
||||||||||||||||||||
напор. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Для реальной жидкости потребуется учёт потерь энергии на внутреннее |
||||||||||||||||||||
трение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
p1 |
+ H1 + |
v1 |
2 |
|
= |
p2 |
+ H 2 |
+ |
v2 |
2 |
+ hпотерь |
|
|
(6) |
||||
|
|
ρg |
|
|
|
|
|
2g |
|
|
|||||||||||
|
|
|
|
|
2g |
|
|
ρg |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
Гидравлический уклон – отношение величины потери напора на участке к длине этого участка.
i = hпотерь . (7)
l
Пьезометрический уклон – отношение изменения суммарного изменения нивелирной высоты и пьезометрического напора на участке к длине этого участка.
|
|
|
|
p |
2 |
|
|
|
|
p |
|
|
|
|
H |
2 |
+ |
|
|
− H |
1 |
+ |
1 |
|
|
||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
i = |
|
|
|
ρg |
|
|
|
ρg |
. |
(8) |
|||
|
|
|
|
|
|
|
|
||||||
Ф |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гидравлический уклон и пьезометрический уклон не что иное, как минимально необходимые тангенсы угла наклона труб.
Режимы движения жидкости
Существует два режима течения жидкости: ламинарный и турбулентный.
Возникновение и структура турбулентности http://www.youtube.com/watch?feature=player_detailpage&v=LC0aIkM5j5g
При ламинарном движении жидкость движется параллельными слоями.
При турбулентном движении жидкость интенсивно перемешивается.
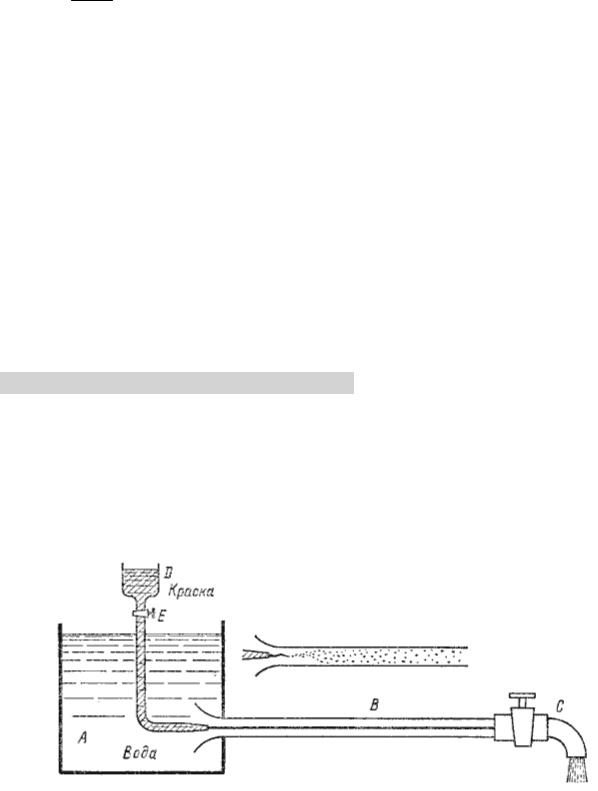
Опыт Рейнольдса (1883 г.)
Рисунок 3 – Опыт Рейнольдса
9

Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.
Ламинарный режим. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени.
Турбулентный режим. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды.
Если уменьшить скорость потока, то восстановится ламинарное течение.
Переход от ламинарного режима к турбулентному и обратно наблюдается при определенной скорости движения жидкости. Эта скорость называется критической vкр.
Значение этой скорости прямо пропорционально вязкости жидкости µ и обратно пропорционально диаметру трубы d и плотности жидкости ρ.
vкр = k μ
ρd
Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Reкр. Как показывает опыт, для труб круглого сечения Reкр примерно равен 2300.
Число Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Reкр течение является ламинарным, а при Re > Reкр течение является турбулентным. Развитое турбулентное течение в трубах устанавливается лишь при Re = 4000, а при Re = 2300…4000 имеет место переходная, критическая область.
Критерий Рейнольдса показывает отношение сил инерции к силам трения, является мерой гидродинамического подобия и определяется следующим образом:
Re = |
vdρ |
, |
(9) |
|
μ |
||||
|
|
|
где v – скорость, d – диаметр трубы, ρ – плотность жидкости, µ – вязкость жидкости.
Чтобы запомнить вэ дэ ро на мю: ведро на метро, ведро молока.
10
