опеределенный игтеграл

y

y = R2 − x2

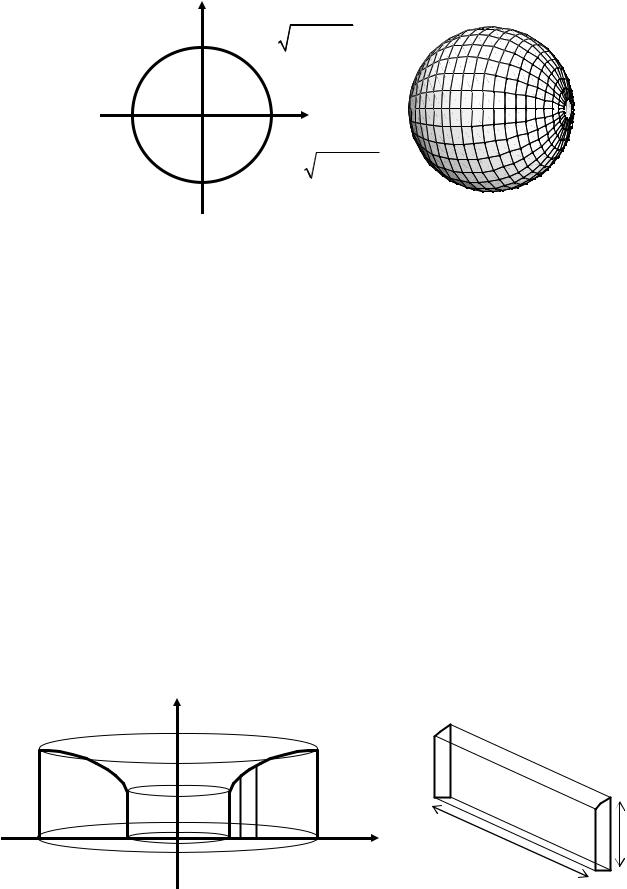
y = − R2 − x2

Рис.23. К выводу формулы объема шара.

Тогда формула (10) приводит к хорошо известному выражению для объема шара:

Вращение вокруг оси OY. В задаче этого типа рассмотренная ранее криволинейная трапеция вращается вокруг оси OY, т.е. вокруг прямой, параллельной основаниям трапеции). Тело вращения имеет кольцевидную форму, а исходная трапеция, по-прежнему, представляет собой половину сечения тела плоскостью OXY (рис.24).

yi

xi

Рис.24. Тело вращения вокруг оси OY.

81

Выделим элементарную трапецию, расположенную над отрезком xi оси

OX. При ее вращении вокруг оси OY возникает кольцо радиуса xi с криволи-

нейным верхним краем. Разрежем его по плоскости OXY и выпрямим. Пренебрегая возникающими незначительными деформациями, получим в результате пластину (рис. 24 б). Заменим эту пластину прямоугольным параллелепипедом (для этого у нее просто отрежем верхний криволинейный край), длина которого

равна 2πxi (длина окружности радиуса xi), ширина xi и высота yi = f ( xi ) . При

малой величине xi объем исходного элементарного кольца приблизительно равен объему полученного параллелепипеда:

Vi ≈ 2πxi yi xi .

Объем тела вращения равен сумме объемов всех элементарных колец:

Vy = ∑ Vi ≈ 2π∑xi yi xi .

i i

После уже не раз проводившегося предельного перехода ( xi → 0, n → ∞) инте-

гральная сумма превратится в определенный интеграл. В результате получим объем тела вращения вокруг оси OY:

a

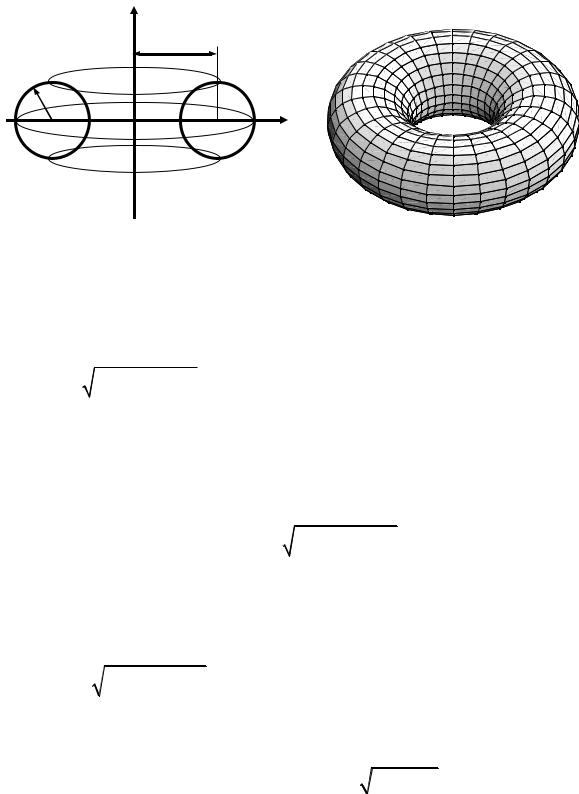
ПРИМЕР 10. Найти объем тора, образованного вращением круга радиуса

R с центром, который удален от оси вращения на расстояние r, где r > R

(рис.25).

Примем ось OY в качестве оси вращения окружности с центром, распо-

ложенном в точке (r, 0) на оси OX, и радиусом R. Уравнение такой окружности имеет вид

(x − r)2 + y2 = R2 .

82

y

r

Рис.25. Тор как тело вращения.

В силу симметрии достаточно рассмотреть вращение только верхней половины круга, граница которого состоит из полуокружности

y = R2 −( x − r)2 .

и отрезка [r − R, r + R] оси OX. Объем полученного тела вращения даст поло-

вину объема тора.

По формуле (11) получаем

Для вычисления интеграла выполним в нем замену переменной:

−π / 2

83

Найдем первый из полученных интегралов, учитывая четность подынтегральной функции:

Второй из интегралов I2 обращается в нуль в силу нечетности подынте-

гральной функции на отрезке интегрирования [−π / 2,π / 2].

Теперь получаем окончательное выражение для объема тора:

Vy = 4π(I1 + I2 ) = 2π2R2r .

84

Теоретические вопросы к главе 2.

1.Как связаны понятия неопределенного и определенного интеграла?

2.Каков геометрический смысл определенного интеграла?

3.Проверить выполнение теоремы о среднем для функции f (x) = x2 на отрезке [1, 2].

π / 2

4. Доказать неравенство ∫ sin(x2 )dx ≤1.

0

−2

5.Найти любую функцию f(x), удовлетворяющую условиям ∫ f (x)dx = 5,

−3

f (–3) = –1.

6.Существует ли непрерывная функция, удовлетворяющая условиям:

1

∫ f (x)dx =1, f (0) = 100, f (1) =100?

0

2

7.Найти любую функцию f (x), удовлетворяющую условиям ∫ f (x)dx = 4 ,

0

f ' (0) = 1 .

x

8.Построить график функции y(x) = ∫ | t | dt .

−2

9. Справедливо ли тождество ∫ f (x) g(x)dx = ∫ f (x)dx ∫g(x)dx ?

10. Существуют ли функции f(x) и g(x) для которых выполнено равенство

∫ f (x) g(x)dx = ∫ f (x)dx ∫g(x)dx ?

2

11. Найти интеграл ∫ 3 sin (x3 )dx .

−2

85

Найти интегралы, используя формулу интегрирования по частям:

87

x = 7(t −sin t),

30.0 ≤ t ≤ 2π .

y = 7(1−cos t),

31.r = 5(3 −cosϕ) .

32.r = e2ϕ , A(0,1), B(2π, e4π ) .

Найти объемы тел вращения фигур, ограниченных линиями

40.r = 2(1+cosϕ) , (вокруг полярной оси).

41.r = cosaϕ , (вокруг полярной оси).

88