
опеределенный игтеграл
.pdf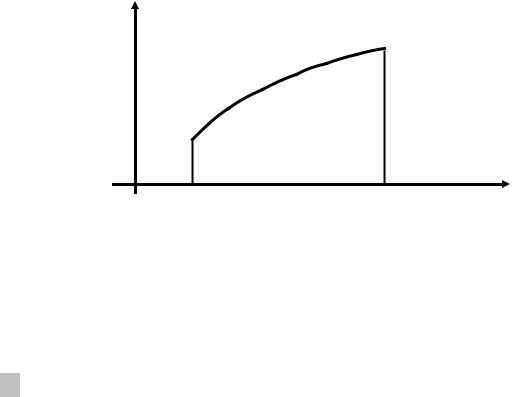
Замечание 2. (Геометрический смысл определенного интегра-
ла). В случае положительной на отрезке [a, b] непрерывной функции f (x) оп-
b
ределенный интеграл ∫ f ( x)dx представляет собой площадь криволинейной a
трапеции, ограниченной сверху графиком функции y = f (x), снизу − осью ОХ,
слева − прямой y = a и справа прямой
y |
y = f ( x), f (x) > 0 |
S = ∫ab f (x)dx
x
a |
b |
Рис.5. Геометрический смысл определенного интеграла.
Сформулируем теперь общие
Свойства определенного интеграла:
n. Для постоянной на [a, b] функции
b |
|
|
∫kdx = k(b −a) . |
(9) |
|
a |
|
|
Доказательство. Все интегральные суммы (2) функции |
f (x) = k яв- |
|
ляются постоянной величиной: |
|
|
n |
n |
|
σn = ∑f (ξi ) xi = |
∑k xi = k( x1 + x2 +…+ xn ) = k(b − a) . |
|
i=1 |
i=1 |
|
Следовательно, и их предел (определенный интеграл) равен той же величине.
51

o. Определенный интеграл от суммы двух интегрируемых функций равен сумме интегралов от этих функций:
b |
b |
b |
|
∫ |
( f (x)+ g(x))dx = ∫ f (x)dx + ∫g(x)dx . |
(10) |
|
a |
a |
a |
|
p. Определенный интеграл тем больше, чем больше функция:
b |
b |
|
f (x)≥ g(x) ∫ f (x)dx ≥ ∫g(x)dx, (a < b). |
(11) |
|
a |
a |
|
q. Если m − наименьшее, а M − наибольшее значения функции f (x) на от-
резке [a, b], где a < b , то
b |
|
m(b −a) ≤ ∫ f (x)dx ≤ M (b −a). |
(12) |
a
(Свойства 2 – 4 легко доказываются на основе определения определенного интеграла и свойств пределов функции).
r. (Теорема о среднем). Для непрерывной на отрезке [a, b] функции f (x)
существует такая точка ξ [a, b], что
b |
|
∫ f (x)dx = f (ξ) (b −a). |
(13) |
a
Доказательство. По свойству 4 при a < b справедливо неравенство m ≤ b −1 a ∫ab f (x)dx ≤ M . Как известно, непрерывная на отрезке [a, b] функция
принимает на этом отрезке любое значение, заключенное между своими наименьшим и наибольшим значениями (см. гл.1 выпуска 2 настоящего пособия).
|
1 |
b |
|
Тогда найдется точка ξ [a, b] такая, что f (ξ) = |
∫ f (x)dx . Отсюда и сле- |
||
b −a |
|||
|
a |
||
|
|
||
дует утверждение теоремы о среднем. |
|
|
52
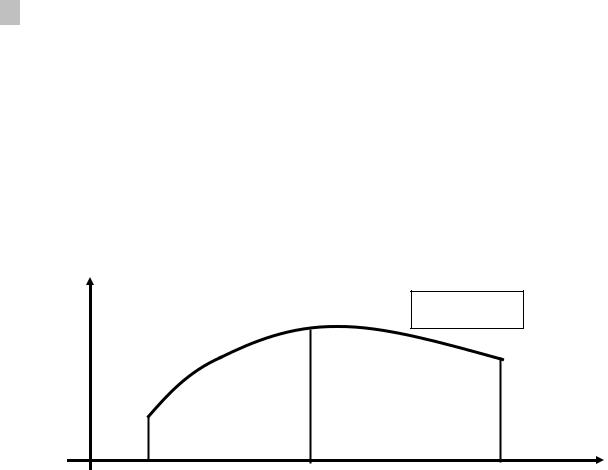
s. Для интегрируемой на отрезке [a, b] функции f (x) и точки с (a, b)
выполняется равенство:
b |
c |
b |
|
∫ f (x)dx = ∫ f ( x)dx + ∫ f (x)dx . |
(14) |
||
a |
a |
c |
|
Геометрическая интерпретация свойства 6 представлена на рис. 6, а доказательство предоставляются читателям для самостоятельной работы.
y |
S = S1 + S2 |
y = f (x) |
S1 = ∫ac f (x)dx |
S2 = ∫cb f (x)dx |
|
a |
|
x |
c |
|
b |
Рис. 6. К свойству 6: S = ∫b |
f (x)dx = S1 + S2. |
|
|
a |
|
До сих пор при записи определенного интеграла мы предполагали, что его нижний предел a меньше верхнего предела b. Для того, чтобы снять этого ограничение, положим по определению (!):
b |
a |
|
∫ f (x)dx = −∫ f (x)dx , (a > b), |
(15) |
|
a |
b |
|
а также |
|
|
a |
|
|
∫ f (x)dx = 0. |
(16) |
|
a
Хотя математические определения и не принято обсуждать, тем не менее, основной довод в пользу того или иного определения состоит в его разумности.
53
Желательно, в частности, чтобы при расширении некоторого понятия на более широкий класс объектов были выполнены свойства, справедливые для более узкого класса. К примеру, именно таким образом в элементарной математике
определили степень с отрицательным показателем: a−n = |
1 |
, (n > 0) , хотя по- |
|
an |
|||
|
|
нятно, что исходное определение степени an = a a a … a в данном случае не n раз
работоспособно: пытаться умножить число a на само себя «минус три раза» бессмысленно. Вместе с тем, при таком определении, оказались справедливыми все свойства степеней с положительными показателями. Точно так же и определения (15) и (16) позволяют сохранить справедливость свойств 1, 2, 5, 6 определенных интегралов вне зависимости от того, какой из пределов интегрирования больше другого. В частности, само свойство (16) немедленно «следует» из (15) при a = b. (В кавычках − потому, что определение (15) не предусматривает возможности совпадения верхнего и нижнего пределов интегрирования).
2.2. Вычисление определенного интеграла.
После данных выше определений можно перейти к вопросу о том, как научиться вычислять определенные интегралы, и как определенные интегралы связаны с неопределенными.
Рассмотрим функцию f (t), непрерывную на отрезке [a, b]. Выберем на интервале (a, b) произвольную точку x. Тогда на отрезке [a, x] существует оп-
ределенный интеграл от функции f (t). (Для того чтобы избежать путаницы с обозначениями переменных, переменную интегрирования будем обозначать через t, сохраняя обозначение x для верхнего предела интеграла). Этот инте-
грал, естественно, зависит не только от вида функции f (t), но и от переменной x, т.е. представляет собой функцию переменной x − верхнего предела интегрирования:
54
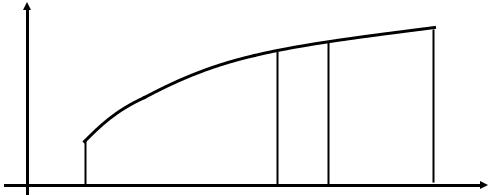
x |
|
Φ(x) = ∫ f (t)dt . |
(1) |
a |
|
Геометрически, в случае положительной функции |
f (t), величина Φ(x) |
представляет собой площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и прямыми t = a и t = b (рис. 7).
y y = f (t)
|
Φ(x) |
|
|
ΔΦ |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
a |
x |
x + |
x |
b |
|
|||
Рис. 7. К вычислению определенного интеграла. |
||||||||
Пусть теперь независимая переменная x получила приращение |
x . Тогда |
|||||||
имеем приращение функции Φ(x): |
|
|
|
|
|
|
||
|
|
x+ |
x |
|
x |
|
|
|
ΔΦ = Φ(x + x) −Φ(x) = ∫ f (t)dt − ∫ f (t)dt . |
|
|
||||||
|
|
a |
|
|
a |
|
|
|
Используя свойства 6 и 5 определенных интегралов, получим |
|
|
||||||
x+Δx |
ξ [x, x + |
x]. |
|
|
||||
ΔΦ = ∫ f (t)dt = f (ξ) x, |
|
(2) |
||||||
x
(На рис. 7 приращение Φ представляет собой площадь фигуры с вертикальной штриховкой).
Теперь, окончательно, можно установить связь понятий неопределенного и определенного интегралов. Эта связь основана на следующих двух теоремах:
55
Теорема 1. Пусть функция f (t) непрерывна на отрезке [a, b], а функция
Φ(x) определена на интервале (a, b) как определенный интеграл
x
Φ(x) = ∫ f (t)dt ,
a
тогда функция Φ(x) представляет собой первообразную функции f (x): |
|
′ |
(3) |
Φ (x) = f (x) . |
Доказательство теоремы немедленно вытекает из равенства (2). Действительно, имеем
′ |
ΔΦ |
|
f (ξ) x |
|
|
Φ (x) = lim |
|
= lim |
|
= lim f (ξ) = f (x) . |
|
x |
x |
||||
x→0 |
x→0 |
x→0 |
Следствие. Следствием из теоремы 1 является утверждение, сформулированное без доказательства при изучении неопределенных интегралов: любая непрерывная функция имеет первообразную. (Первообразная непрерывной функции f (x) может быть получена по формуле (1)).
Теорема 2. (Формула Ньютона − Лейбница). Если функция F(t) яв-
ляется первообразной непрерывной функции f (x), то
b |
|
∫ f (x)dx = F(b) − F(a) . |
(4) |
a
Доказательство. По теореме 1 функция Φ(x), определенная по форму-
ле (1), также является первообразной для f (x). Следовательно, по теореме о первообразных (см. главу 1) функции Φ(x) и f (x) отличаются на постоянную величину:
Φ(x) − F( x) = C = const .
Имеем при x = a:
C = Φ(a) − F(a) = −F(a) .
Тогда
56
Φ(x) = C + F( x) = F(x) − F(a) .
Теперь при подстановке в последнее равенство значения x = b, получим
Φ(b) = F(b) − F(a) ,
что, по определению функции Φ(x), приводит к равенству (4).
Формула Ньютона − Лейбница позволяет вычислять определенные интегралы для функций, первообразные которых известны.
|
1 |
|
|
x |
6 |
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||||||
ПРИМЕР 1. |
∫x5dx = |
|
|
|
|
= |
−0 = |
. |
|||||
6 |
|
|
0 |
6 |
6 |
||||||||
|
0 |
|
|
|
|
|
|
|
|||||
|
−e |
dx |
|
|
|
|
|
|
−e = ln | −e | −ln | −1 |= ln e −ln1 =1. |
||||
|
|
|
|
|
|
|
|||||||
ПРИМЕР 2. |
∫ |
= ln | x | |
|||||||||||
|
−1 |
x |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИМЕР 3. |
Вычислить определенный интеграл ∫2 xe−x2 dx . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Здесь удобнее вначале найти первообразную (неопределенный интеграл):
∫xe−x2 dx = − |
1 |
∫e−x2 d (−x2 )=− |
|
1 |
e−x2 |
+C . |
|
|
|||||||||
2 |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
1 |
2 |
|
2 |
1 |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 = − |
|
|
|
|
|
||||||
∫0 |
xe−x |
|
dx = − 2 e−x |
|
|
|
2 (e−4 −1)= |
2 (1 −e−4 ). |
|||||||||
ПРИМЕР 4. Найти ∫π sin nx sin mx dx , (m и n − целые). |
|||||||||||||||||
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
Для случая n ≠ m имеем: |
|
|
|
|
|
|
|
|
|
|
|
||||||
∫π |
|
sin nx sin mx dx = |
1 |
∫π (cos(n −m)x −cos(n + m)x)dx = |
|||||||||||||
−π |
|
|
|
|
|
2 |
−π |
|
|
|
|
|
|
|
|
||
|
|
|
|
= |
1 sin(n −m)x |
|
π |
1 sin(n + m)x |
|
π |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 n |
−m |
|
− |
2 n +m |
|
= 0. |
|||||||
|
|
|
|
|
|
−π |
|
−π |
|||||||||
57
При n = m интеграл вычисляется иначе: |
|
|
|||||||||||
∫π |
sin2 nx dx = |
1 |
|
∫π |
(1−cos 2x)dx = |
|
|||||||
−π |
|
|
2 |
−π |
|
|
|
|
|
|
|
|
|
|
= |
1 |
x |
|
π |
− |
1 |
sin 2x |
|
π |
= |
1 |
(π −(−π)) =π. |
|
|
|
|||||||||||
|
2 |
|
−π |
4 |
|
−π |
2 |
||||||
|
|
|
|
|
|
|
|
|
|||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
sin nx sin mx dx |
0, |
n ≠ m |
|
|
|
|||||||
∫−π |
= |
|
n = m |
|
|
|
|||||||
|
|
|
|
π, |
|
|
|
||||||
(Заметим, что если определить скалярное произведение двух функций f (x) и g (x) на отрезке [ a, b] с помощью формулы
( f , g) = ∫ab f (x)g(x) dx ,
то полученный в примере результат свидетельствует об ортогональности
функций sin nx и sin mx на отрезке [ – π, π ] при n ≠ m).
Теорема 3. (Замена переменной в определенном интеграле).
Пусть f (x) − непрерывная на отрезке [a, b] функция, а функция x = ϕ (t)
непрерывно дифференцируема на отрезке [to , t1] |
и удовлетворяет на концах |
|
этого отрезка условиям: ϕ (tо) = a, ϕ (t1) = b. Тогда справедлива формула |
||
b |
t1 |
|
|
′ |
(5) |
∫ f (x)dx = ∫ f (ϕ(t))ϕ (t)dt . |
||
a |
to |
|
Доказательство. Пусть функция F(x) является первообразной для |
||
функции f (x), т.е. |
∫ f (x)dx = F(x) +C . Тогда, по формуле для замены пере- |
|
менной в неопределенном интеграле, ∫ f (ϕ(t))ϕ |
′ |
|
(t)dt = F(ϕ(t))+C . Теперь, |
||
используя формулу Ньютона − Лейбница, получаем требуемое утверждение:
58
t1 |
|
t1 |
|
|
|
||
∫ |
′ |
= F (ϕ(t1)) − F(ϕ(to )) = |
|
f (ϕ(t))ϕ (t)dt = F(ϕ(t)) |
to |
||
ro |
|
|
|
|
|
b
= F(b) − F(a) = ∫ f (x)dx.
a
11
ПРИМЕР 5. Найти определенный интеграл ∫ x x −2 dx .
3
Для устранения иррациональности в интеграле удобно выполнить замену
переменной |
x −2 = t . Тогда по формуле (5) получаем |
|
||||||||||||||||||
11 |
|
|
x = 2 +t2 , |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dx = 2t dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫ |
x x −2dx = |
|
= ∫(2 +t2 )t 2t dt = |
|||||||||||||||||
3 |
|
|
x = 3 t =1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x =11 t = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
(4t |
2 |
+ 2t |
4 |
) dt |
|
4 |
t |
3 |
|
3 |
|
2 |
t |
5 |
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
= ∫ |
= |
|
+ |
|
= |
||||||||||||||
|
|
|
3 |
|
|
1 |
5 |
|
|
1 |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 43 (33 −1) + 52 (35 −1) = 197215 .
Замечание. Отметим, что при всей схожести применения формул замены переменной в неопределенном и определенном интегралах, имеется весьма важное их отличие: при вычислении определенного интеграла не нужно возвращаться к исходной переменной, вместо этого просто производится соответствующее изменение пределов интегрирования.
a
ПРИМЕР 6. Вычислить определенный интеграл ∫ a2 − x2 dx.
0
Здесь для вычисления интеграла удобно выполнить тригонометрическую подстановку, которая позволяет избавиться от иррациональности:
59

a
∫
0
x = a sin t,
a2 − x2 dx == dx = a cos t dt. x = 0 t = 0
x = a t =π / 2
π / 2
= ∫ a2 −a2 sin2 t a cos t dt =
0
π / 2 |
π / 2 |
1+cos 2t |
dt = |
a2 |
|
|
π / 2 |
sin 2t |
|
π / 2 |
|
= |
πa2 |
. |
|
|
|||||||||||||
|
||||||||||||||
= a2 ∫ |
cos2 t dt =a2 ∫ |
2 |
2 |
t |
|
+ |
2 |
|
|
|
4 |
|||
|
|
|
|
|
0 |
|
0 |
|
|
|
||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Сформулируем еще один прием вычисления определенных интегралов, аналогичный уже рассмотренному в главе 1 для неопределенных интегралов.
Теорема 4. (Интегрирование по частям в определенном интеграле).
Пусть функции u(x) и v(x) − непрерывны и имеют непрерывные произ-
водные. Тогда
|
b |
|
|
b |
b |
|
|
|
|
∫udv = (uv) |
|
a |
− ∫vdu . |
|
(6) |
|
|
|
a |
|
|
a |
|
|
|
|
Доказательство. |
|
|
′ |
′ |
′ |
|||
Проинтегрируем обе части равенства (uv) |
= u v + uv |
|
||||||
по переменной x в пределах от a до b: |
|
|
||||||
b |
′ |
b |
|
b |
|
|
|
|
|
′ |
|
′ |
dx . |
|
|
||
∫(uv)dx = ∫u vdx + ∫uv |
|
|
||||||
a |
|
a |
|
a |
|
|
|
|
Интеграл в левой части может быть найден по формуле Ньютона−Лейбница, а
|
|
|
|
′ |
′ |
правая часть преобразована с учетом равенств du = u dx, |
dv = v dx : |
||||
(uv) |
|
b |
b |
b |
|
|
|
||||
|
= ∫vdu + ∫u dv . |
|
|||
|
|
a |
a |
a |
|
|
|
|
|
||
Отсюда и получаем формулу (6).
60
