
53.Несобственные интегралы 1-го и 2-го рода
..pdf§1. Несобственные интегралы по бесконечному промежутку (первого рода)
Эти интегралы называются также интегралами с бесконечными пределами.
Пусть функция f (x) определена на бесконечном промежутке [a, ) и интегрируема
на всяком конечном промежутке |
[a, b] [a, ) . Если существует |
конечный или |
||
b |
|
|
|
|
бесконечный предел lim f ( x) dx , |
то он называется несобственным интегралом первого |
|||
b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
рода от функции f (x) по промежутку [a, ) и обозначается символом |
f ( x) dx . Таким |
|||
|
|
|
|
a |
образом, по определению |
|
|
|
|
|
|
|
b |
|
|
|
f ( x) dx lim |
f ( x) dx . |
(1.1) |
|
a |
b |
a |
|
|
|
|
||
Аналогично |
|
|
|
|
|
b |
|
b |
|
|
|
f ( x) dx lim |
f ( x) dx , |
(1.2) |
|
|
a |
a |
|
|
|
|
||
|
|
|
b |
|
|
|
f ( x) dx lim |
f ( x) dx . |
(1.3) |
|
|
a |
|
|
|
b a |
|
||
(В формуле (1.3) переменные a и b стремятся к своим пределам независимо). |
||||
Предполагается, что функция |
f (x) интегрируема на всяком конечном промежутке, |
|||
входящем в соответствующих бесконечный промежуток, и существуют конечные или бесконечные пределы (1.1) – (1.3). Эти пределы и называются несобственными интегралами первого рода. Говорят также в случае конечных пределов (1.1) – (1.3), что соответствующий интеграл сходится. Если предел не существует или бесконечен, то рассматриваемый интеграл называется расходящимся. В случае, когда пределы (1.1) – (1.3) не существуют (ни как конечные, ни как бесконечные). соответствующий несобственный интеграл понимается лишь как символ.
В дальнейшем для простоты будем предполагать, что подынтегральная функция является непрерывной в соответствующем бесконечном промежутке. Этого достаточно для большинства приложений.
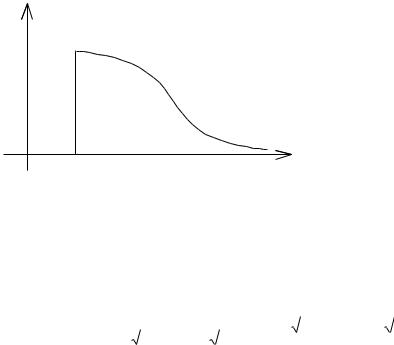
|
y |
Геометрический |
смысл |
несобственного |
||||
|
интеграла первого рода. |
|
|
|
||||
|
y f (x) |
|
|
|
||||
|
Если |
f (x) 0 , |
то несобственный интеграл |
|||||
|
|
|||||||
|
|
первого рода численно равен площади бесконечной |
||||||
|
|
криволинейной |
трапеции, |
опирающейся |
на |
|||
|
x |
промежуток |
интегрирования. |
Для |
интеграла |
по |
||
O |
a |
промежутку |
[a, ) |
такая криволинейная трапеция |
||||
Рис. 1.1. Бесконечная криволинейная |
изображена на рис. 1.1. |
|
|
|
||||
|
трапеция с основанием [a, ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
Примеры.
dx |
b |
dx |
|||
1.1. |
x |
2 |
lim |
x |
2 |
1 |
|
1 |
|
||
|
|
|
b |
|
|
|
|
1 |
|
b |
|
|
|||||
lim |
x |
|
|
||
b |
|
|
1 |
|
|
|
|
|
|
1
lim 1 1. Интеграл сходится.
b b
dx |
|
|
b |
dx |
|
|
|
|
|||
1.2. |
|
|
|
lim |
|
|
|
|
|
lim |
2 |
|
|
|
|
|
|
||||||
1 |
|
x |
|
b |
1 |
|
x |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
x |
lim |
2 |
b 2 |
. Интеграл расходится. |
||||||
|
|
|
|
|||||||
|
|
|
1 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dx |
b |
dx |
|
|
b |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
1.3. |
|
|
|
lim |
|
|
lim |
arctg x |
|
|
lim (arctg b arctg a) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
1 |
x2 |
a 1 |
x2 |
a |
|
a |
|
a |
2 |
|
|
2 |
|
||
|
|
|
|
|||||||||||||
|
|
|
b a |
|
b |
|
|
|
b |
|
|
|
|
|
||
Интеграл сходится.
Замечание 1.1. Несобственный интеграл (1.3) может рассматриваться как сумма двух интегралов по промежуткам ( , a] и [a, ) , где a – любое число. Интеграл (1.3)
сходится тогда и только тогда, когда сходятся оба слагаемых интеграла.
