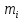3. Медиана

Медианой (Me) называется значение признака, которое лежит в середине ранжированного ряда. Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.

В дискретном ряду медиана находится на основе накопленных частот. Номер медианы равен половине суммы всех частот. Частоты накапливаются до тех пор, пока не будет превзойдён номер медианы. Медиана равняется частоте, соответствующей номеру медианы.

В интервальном ряду сначала находится медианный интервал. Номер медианы равен 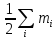или. По номеру определяется интервал, которому этот номер принадлежит. Затем медиана определяется по формуле:

где

x_k-1 – нижняя граница медианного интервала;

h_k – длина медианного интервала;

F_k-1 – накопленная частота интервала, предшествующему медианному;

m_k – частота медианного интервала;

P_k-1 – накопленная частость интервала, предшествующему медианному.

Если требуется найти медиану в ранжированном ряду без частот, то номер медианы можно определить по формуле (N+1)/2, если ряд содержит нечётное число элементов. Затем по номеру медианы выбирается медиана из значений признака. Если ряд содержит четное число элементов, то медиана вычисляется по формуле:

где

N – число элементов в ряду.

В интервальном ряду медиана определяется по кумуляте. Для этого из точки на шкале накопленных частот (частостей), соответствующей , проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем на ось абсцисс опускается перпендикуляр. Абсцисса точки пересечения является медианой.

Пример 15. Вычисление медианы для дискретного вариационного ряда

Найти медиану для распределения сотрудников по тарифным разрядам.

Тарифный разряд	Число сотрудников, чел	Накопленная частота
2	11	11
3	18	29
4	22	51
5	20	71
6	14	85
Итого	85

Ряд является дискретным. Номер медианы равен 42 или 43 (85/2). Накапливать частоты нужно до тех пор, пока не будет превзойдён номер медианы: 11 сотрудников имеют не более, чем 2 разряд; 29 сотрудников имею не более, 3 разряд; 51 сотрудник имеет не более, чем 4 разряд. Т.е. число сотрудников 42 и 43 приходится на 4 разряд. Следовательно, Me=4.

Пример 16. Вычисление медианы для интервального вариационного ряда с равной длиной интервалов

Найти медиану для распределения сотрудников по возрастам.

Возрастные группы сотрудников, лет	Число сотрудников, чел	Накоплен- ные частоты	Частости		Накопленные частости
			в долях	в %	в долях	в %
20 – 30	11	11	0,1294	12,94	0,1294	12,94
30 – 40	33	44	0,3882	38,82	0,5176	51,76
40 – 50	22	66	0,2588	25,88	0,7764	77,64
50 – 60	15	81	0,1765	17,65	0,9529	95,29
60 – 70	4	85	0,0471	4,71	1	100
Итого	85		1	100

Ряд является интервальным. Номер медианы, рассчитанный на основе накопленных частот, равен 42 или 43 (85/2), а накопленный на основе частостей равен 50 (100/2). На основе накопленных частот определяется, что числу сотрудников 42 и 43 соответствует возрастной интервал 30 – 40. Далее находится медиана:

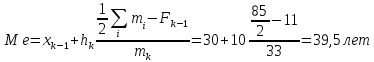
Графическое определение медианы:

Пример 17. Вычисление медианы ранжированного ряда с нечетным числом интервалов

Найти медиану для ранжированного ряда, в котором представлены набранные баллы участников конкурса.

Место	Фамилия	Баллы
1	Иванов	135
2	Смирнов	117
3	Петров	98
4	Сидоров	89
5	Фёдоров	64
6	Макаров	57
7	Казаков	53

В таблице нечётное число элементов. Номер медианы равен ((7+1)/2)=4. Этому номеру соответствует медиана M_e = 89 баллов.

Пример 18. Вычисление медианы ранжированного ряда с нечетным числом интервалов

Найти медиану для ранжированного ряда, в котором представлены набранные баллы участников конкурса.

Место	Фамилия	Баллы
1	Иванов	135
2	Смирнов	117
3	Петров	98
4	Сидоров	89
5	Фёдоров	64
6	Макаров	7

В таблице чётное число элементов. Медиана вычисляется по формуле: