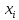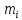3.3.3. Средняя геометрическая

Средняя геометрическая выводится при подстановке в формулу степенной средней значения z=0.

После раскрытия неопределённостей получаются формула средней геометрической простой:

и формула средней геометрической взвешенной:

Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста.

3.3.4. Средняя квадратическая

Средняя квадратическая вычисляется при подстановке в формулу степенной средней z=2.

Для несгруппированных данных используется формула средней квадратической простой:

Для сгруппированных данных применяется формула средней квадратической взвешенной:

Средняя квадратическая применяется при изучении вариации признака, в качестве вариантов используются отклонения фактических значений признака или от средней арифметической, или от заданной нормы.

4. Вариационные ряды

Наличие различий в значениях признака у единиц совокупности называется вариацией признака. Для того, чтобы определить закономерности в этом распределении, строят ряды распределения единиц совокупности по какому-либо варьирующему признаку.

Вариационный ряд – групповая таблица, построенная по количественному признаку, в сказуемом которой показывается число единиц в каждой группе.

По способу построения различают дискретные и интервальные вариационные ряды.

Дискретный вариационный ряд строится для признака, имеющего прерывное изменение, (число компьютеров, тарифный разряд рабочего) и принимающего небольшое количество значений. Для признака, имеющего непрерывное изменение (возраст, размер дохода) или непрерывное с большим количеством значений, строится интервальный вариационный ряд.

Самые простые вариационные ряды состоят из двух граф – варианты и частоты. Примеры самых простых вариационных рядов приведены в таблицах 6, 7 и 8.

Таблица 6. Распределение сотрудников по квалификации (пример дискретного вариационного ряда)

Тарифный разряд	Число сотрудников, чел
2	11
3	18
4	22
5	20
6	14
Итого	85

Таблица 7. Распределение сотрудников предприятия по возрастным группам (пример интервального вариационного ряда с равным числом интервалов)

Возрастные группы сотрудников, лет	Число сотрудников, чел
20 - 30	11
30 - 40	33
40 – 50	22
50 – 60	15
60 - 70	4
Итого	85

Таблица 8. Распределение количества фермерских хозяйств по численности поголовья скота (пример интервального вариационного ряда с неравным числом интервалов)

Поголовье скота, шт	Количество хозяйств, шт
Менее 5	11
5 - 10	33
10 – 30	22
30 – 50	15
50 - 100	4
Итого	85

Вариационные ряды могут дополняться другими графами, необходимыми для вычисления каких-либо статистических показателей. Часто вводится графа, в которой подсчитываются накопленные частоты. Накопленные частоты (F) показывают, сколько единиц совокупности имеет значение признака не больше, чем данное значение, и вычисляются путём последовательного прибавления к частоте первого интервала частот последующих интервалов:

Иногда частоты ряда (m) заменяются частостями. Частости (w) представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путём деления частоты каждого интервала на их общую сумму:

Частости обычно применяют, когда совокупность очень велика. Кроме того, они позволяют сравнивать распределения по одному и тому же признаку в разных по численности совокупностях. Частости накапливаются аналогичным образом.

Используются также такие показатели, как доля признака в общей сумме признаков идоля признака в общей сумме признаков нарастающим итогом (q):

и т.д.

Если вариационный ряд составлен с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчёт абсолютной или относительной плотности распределения (y).

Абсолютная плотность распределения (y_i) – частота, приходящаяся на единицу длины интервала:

Относительная плотность распределения (y_i) – частность, приходящаяся на единицу длины интервала:

где

w_i – частость;

h_i – длина i-го интервала.

Пример 8. Вычисление накопленных частот, частостей в долях и процентах, накопленных частостей в долях и процентах

Для распределения сотрудников по тарифным разрядам высчитать накопленные частоты, частости в долях и процентах, накопленные частости в долях и процентах (Таблица 9).

Таблица 9. Распределение сотрудников по тарифным разрядам

Тарифный разряд	Число сотрудников, чел	Накоплен- ные частоты	Частости		Накопленные частости
			в долях	в %	в долях	в %
2	11	11	0,1294	12,94	0,1294	12,94
3	18	29	0,2118	21,18	0,3412	34,12
4	22	51	0,2588	25,88	0,6	60
5	20	71	0,2353	23,53	0,8353	83,53
6	14	85	0,1647	16,47	1	100
Итого	85		1	100

Накопленные частоты:

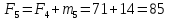
Частости в долях:

0,1294

Частости в процентах:

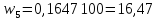
Накопленные частости в долях:

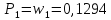
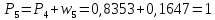
Накопленные частости в процентах:

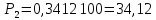
Пример 9. Вычисление накопленных частот, частостей в долях и процентах, накопленных частостей в долях и процентах

Для распределения сотрудников по возрастным группам высчитать накопленные частоты, частости в долях и процентах, накопленные частости в долях и процентах (Таблица 10).

Таблица 10. Распределение сотрудников по возрастным группам

Возрастные группы сотрудников, лет	Число сотрудников, чел	Накоплен- ные частоты	Частости		Накопленные частости
			в долях	в %	в долях	в %
20 – 30	11	11	0,1294	12,94	0,1294	12,94
30 – 40	33	44	0,3882	38,82	0,5176	51,76
40 – 50	22	66	0,2588	25,88	0,7764	77,64
50 – 60	15	81	0,1765	17,65	0,9529	95,29
60 – 70	4	85	0,0471	4,71	1	100
Итого	85		1	100

Накопленные частоты:

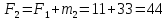
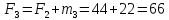
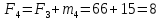
Частости в долях:

Частости в процентах:

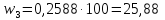
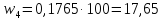
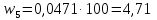
Накопленные частости в долях:

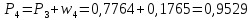
Накопленные частости в процентах:

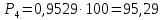
Пример 10. Вычисление абсолютной плотности распределения для интервального ряда с неравной длиной интервалов

Для распределение количества фермерских хозяйств по численности поголовья скота вычислить абсолютную плотность распределения (Таблица 11).

Таблица 11. Распределение количества фермерских хозяйств по численности поголовья скота

Поголовье скота, шт xi	Количество хозяйств, шт mi	Абсолютная плотность распределения yi
Менее 5	11	2,2
5 – 10	33	6,6
10 – 30	22	1,1
30 – 50	15	0,75
50 –100	4	0,08
Итого	85

Абсолютная плотность распределения:

Пример 11. Вычисление доли признака в общей сумме признаков, доли признака в общей сумме признаков нарастающим итогом и доли признака в общей сумме признаков нарастающим итогом в % для интервального ряда с равной длиной интервалов

Для распределения сотрудников по возрастным группам высчитать долю признака в общей сумме признаков, долю признака в общей сумме признаков нарастающим итогом и долю признака в общей сумме признаков нарастающим итогом в % (Таблица 11).

Таблица 12. Распределение сотрудников по возрастным группам

Возрастные группы сотрудников, лет	Число сотрудников, чел	Середина интервала, xiср		Доля признака в общей сумме признаков
					нарастающим итогом	нарастающим итогом, %
20 – 30	11	25	75	0,08	0,08	8
30 – 40	33	35	1155	0,33	0,41	41
40 – 50	22	45	990	0,28	0,69	69
50 – 60	15	55	825	0,24	0,93	93
60 – 70	4	65	260	0,07	1	100
Итого	85		3505	1

Доля признака в общей сумме признаков:

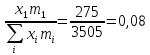
Доля признака в общей сумме признаков нарастающим итогом:

Доля признака в общей сумме признаков нарастающим итогом в %: