
- •Оглавление
- •Статистическое наблюдение
- •Группировка и сводка статистических данных
- •Обобщающие статистические показатели
- •3.1. Абсолютные величины
- •3.2. Относительные величины
- •3.3. Средние величины
- •3.3.1. Средняя арифметическая
- •3.3.1.1. Метод отсчёта от условного нуля
- •3.3.2. Средняя гармоническая
- •3.3.3. Средняя геометрическая
- •3.3.4. Средняя квадратическая
- •Вариационные ряды
- •Основные показатели вариационных рядов
- •Показатели среднего уровня
- •Средние степенные
- •Медиана
- •Показатели степени вариации
- •4.1.2.6. Виды дисперсий
- •4.1.2.6.1. Правило сложения дисперсий
- •4.1.2.6.2. Эмпирическое корреляционное отношение
- •4.1.2.6.3. Правило сложения дисперсий для доли признака
- •4.1.3. Показатели дифференциации и концентрации
- •4.1.3.1. Показатели дифференциации
- •20 – 30
- •50 – 60
- •4.1.3.2. Показатели концентрации
- •4.1.4. Показатели формы распределения
- •4.1.4.1. Моменты распределения
- •4.1.4.1.1. Начальные моменты
- •4.1.4.1.2. Условные моменты
- •4.1.4.1.3. Центральные моменты
- •4.1.4.2. Показатели асимметрии распределения
- •4.1.4.3. Показатели крутизны распределения
- •4.1.5. Кривые распределения
- •Нормальное распределение
- •Распределение Пуассона
- •Критерии согласия
- •Критерий согласия Пирсона
- •Критерий согласия Романовского
- •Критерий согласия Колмогорова
4.1.4.3. Показатели крутизны распределения
Для вычисления показателя крутизны распределения используется центральный момент четвёртого порядка

Чтобы
показатель крутизны не зависел от
выбранного при измерении масштаба,
вводится нормированный
момент четвёртого порядка
или коэффициент
крутизны ( )
– отношение центрального момента
четвёртого порядка к среднему
квадратическому отклонению, возведённому
в четвёртую степень.
)
– отношение центрального момента
четвёртого порядка к среднему
квадратическому отклонению, возведённому
в четвёртую степень.

При
оценке крутизны в качестве эталонного
выбирается нормальное распределение,
для которого
 .
Для сравнения данного распределения с
нормальным используетсяэксцесс
распределения
.
Для сравнения данного распределения с
нормальным используетсяэксцесс
распределения

Если Ex > 0, то распределение высоковершинное, если Ex < 0, то распределение низковершинное.

Пример 25. Вычисление коэффициента асимметрии и нормированного момента третьего и четвертого порядков
Для данных таблицы найти коэффициент асимметрии и нормированные моменты третьего и четвёртого порядка.
|
Величина всходов, см xi |
Количество всходов, шт mi |
Середина интервала, см xiср |
ximi |
|
|
|
|
0 – 5 |
9 |
2,5 |
22,5 |
4029,06 |
-85248,14 |
1803705,74 |
|
5 – 10 |
16 |
7,5 |
120 |
4178,45 |
-67500,51 |
1090693,63 |
|
10 – 15 |
29 |
12,5 |
362,5 |
3610,72 |
-40289,53 |
449562,74 |
|
15 – 20 |
42 |
17,5 |
735 |
1592,84 |
-9808,17 |
60407,80 |
|
20 – 25 |
49 |
22,5 |
1102,5 |
65,93 |
-76,15 |
88,20 |
|
25 – 30 |
43 |
27,5 |
1182,5 |
634,62 |
2438,03 |
9366,16 |
|
30 – 35 |
33 |
32,5 |
1072,5 |
2579,80 |
22809,78 |
221677,20 |
|
35 – 40 |
21 |
37,5 |
787,5 |
4023,45 |
55691,32 |
770862,43 |
|
40 – 45 |
13 |
42,5 |
552,5 |
4615,12 |
86956,80 |
1638413,75 |
|
45 – 50 |
4 |
47,5 |
190 |
2273,71 |
54209,02 |
1292435,21 |
|
Итого |
259 |
|
6127,5 |
27602,51 |
19181,45 |
7317212,86 |
Средняя арифметическая:

Среднее квадратическое отклонение:

Центральный момент третьего порядка:

Нормированный момент третьего порядка:

Нормированный момент третьего порядка (коэффициент асимметрии) >0. Следовательно, асимметрия положительная и имеет место правосторонняя скошенность, т.е. всходов, имеющих размер больше 15 см больше, чем всходов, имеющих размер меньше 10 см.
Модальный интервал 20 – 25, т.к. ему соответствует максимальная частота 49.
Мода:

Коэффициент асимметрии Пирсона:

Коэффициент асимметрии Пирсона также положительный. Это является доказательством того, что скошенность правосторонняя.
Центральный момент четвёртого порядка:

Нормированный момент четвёртого порядка:
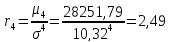
Эксцесс распределения:

Эксцесс распределения отрицательный, поэтому распределение низковершинное.
4.1.5. Кривые распределения
Чем больше количество наблюдений и меньше величина интервала, тем лучше видны закономерности распределения, а представляющая полигон частот ломаная линия ближе приближается к некоторой плавной линии. В пределе она должна превратиться в кривую линию.
Кривая линия, отражающая закономерность изменения частот в исключающем влияние случайных факторов виде, называется кривой распределения. Кривая распределения может рассматриваться как теоретическая (вероятностная) форма распределения, присущая определённой совокупности и может использоваться в различных расчётах и прогнозах.
В настоящее время изучено большое количество форм распределения. Очень важно выдвинуть верную гипотезу о типе кривой распределения. В статистических исследованиях наиболее часто используются нормальное распределение и распределение Пуассона.



